

通过自适应滤波器进行降噪的设计
模拟技术
描述
1 引言
降噪耳机是降噪技术的一个重要应用。我国的降噪技术研究始于 80 年代初期,采用的手段主要有三种,其中的动态降噪技术(DNR)又可以分为模拟动态降噪技术和数字动态降噪技术。目前国内外解决噪声问题最普遍的方法是采用模拟动态降噪技术,数字降噪技术的研究尚处于初期阶段。数字降噪技术比模拟降噪技术具有更大的优点。模拟降噪技术全采用硬件实施,修改和调试十分困难,对元器件参数的变化也很敏感,技术指标受元器件的误差影响较大,降噪效果不稳定,不利于产品的批量生产。而数字降噪技术由于采用计算机技术实现自适应滤波,通过修改软件算法就可以达到不同的降噪效果,不用更改硬件结构,调试和维修都非常方便;数字降噪技术采用自适应滤波技术,可以实时跟踪噪声的变化进一步进行处理,因此降噪效果较好。另外,数字降噪技术抗干扰能力强,本身具有自恢复能力,并且在整个音频带内降噪比较均衡,而模拟降噪技术偏重于低频段,高频段效果较差。因此降噪技术未来的发展方向是数字降噪技术,以数字信号处理(DSP)及其相关算法为技术支撑的数字降噪技术代表着当今降噪技术的发展。
目前市场上的降噪耳机产品主要是模拟降噪耳机,数字降噪耳机只有日本 SONY 公司开发的一款产品,因此数字降噪耳机的设计在国内属于领先技术。数字降噪耳机的系统原理是通过数字降噪耳机中的麦克风装置直接检测出噪声信号和音频信号的混合信号,然后将混合信号通过dsp 数字降噪模块进行噪声分离并产生降噪信号来抵消噪声,因此人耳就可以只听到较纯净的音频信号而不受环境噪声的干扰。本文采用最小均方误差(LMS)算法,实现了数字降噪DSP 中消除噪声的模块自适应滤波器的设计,介绍了其在MATLAB 中Simulink建模及仿真输出,并通过程序实现了设计。
2 自适应滤波器设计原理和结构
数字降噪耳机中 DSP 数字降噪模块是通过自适应滤波器来实现的,自适应滤波器具有跟踪信号和噪声变化的能力,滤波器的特性也随信号和噪声的变化而变化,以达到最优滤波效果。自适应滤波器可以利用前一时刻获得的滤波器系数,自动地调节滤波器参数,以适应信号和噪声位置的统计特性,从而实现最优滤波。自适应滤波器的研究始于20 世纪50 年代末,是关于信号处理方法和技术的滤波器。自适应滤波器能够得到比较好的滤波性能,当输入信号的统计特性变化时,自适应滤波器能够自动的迭代调节自身的滤波器参数,以满足某种准则的要求,从而实现最优滤波。自适应滤波器的特性变化是由自适应算法通过调整滤波器的系数实现的。所以,自适应滤波器一般都由两部分组成:一是参数可调的数字滤波器结构,它是为完成期望的处理功能而设计;二是自适应算法,它调节滤波器系数以改进性能。自适应滤波器结构图如图1 所示。
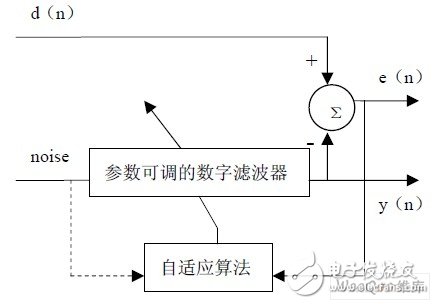
图1:自适应滤波器结构图一般形式
图 1 中,噪声信号通过参数可调的滤波器后产生输出信号y(n),d (n)表示期望信号,由音频信号和噪声混合组成,y(n)与期望信号d (n)进行比较,得到误差信号e(n)。e(n) 和噪声通过自适应算法对滤波器的参数进行调整,使自适应滤波器输出效果达到最好。重复上面过程,滤波器逐渐了解到关于输入信号和噪声的统计规律,并以此为根据自动调整自己的参数,从而达到最佳的滤波效果。一旦输入信号的统计规律发生了变化,滤波器能够自动跟踪输入信号的变化,自动调整滤波器的参数,最终达到滤波效果,实现自适应过程。当噪声信号和混有噪声的音频信号通过自适应滤波器之后,可以将环境中的噪声分离出来,并且自适应跟踪环境噪声变化,进而产生降噪信号从而实现噪声消除。
3 自适应算法
自适应滤波器除包括按照某种结构设计的数字滤波器外,还有一套自适应的算法。自适应算法是根据某种判断来设计滤波器的,其目标是使某一特定的函数最小化。自适应算法的种类很多,根据其优化准则的不同可分为两类最基本的算法:最小均方误差(LMS)算法和递推最小二乘(RLS)算法。本文采用最常用的著名的最小均方误差算法,即LMS 算法,这是由Widrow 和Hoff 提出的,是一种易于实现、性能稳健、应用广泛的算法,其目标是通过调整系数,使输出误差序列的均方值最小化,并且根据这个判据来修改权系数。LMS 滤波算法写成矩阵的形式为:
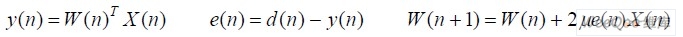
式中,W(n)为n 时刻自适应滤波器的权矢量;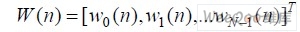 ,N 为自适应滤波器的阶数; X(n)为n 时刻自适应滤波器的参考输入矢量,由最近N 个信号采样值构成,
,N 为自适应滤波器的阶数; X(n)为n 时刻自适应滤波器的参考输入矢量,由最近N 个信号采样值构成,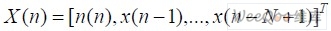 。d (n)是期望的输出值;e(n)为自适应滤波器的输出误差调节信号(简称失调信号);μ 是控制自适应速度与稳定性的增益常数,又叫收敛因子或步长因子。
。d (n)是期望的输出值;e(n)为自适应滤波器的输出误差调节信号(简称失调信号);μ 是控制自适应速度与稳定性的增益常数,又叫收敛因子或步长因子。
4 MATLAB 建模及仿真分析
数字降噪耳机可以在很多场合将音频信号中包含的外界环境噪声进行噪声消除。一个标准音频信号往往包含着许多外界环境中的噪音,而由于噪音的随机性和不可预测性,使得所期望得到的信号不再是周期性的标准信号。使用LMS 算法的自适应滤波器能够自适应的进行信号分离,分离出信号中的噪声成分,然后对其反相产生抵消噪声的降噪信号与噪声信号对消,以达到去掉噪声的目的。下面用MATLAB 中的Simulink 工具对数字降噪耳机中DSP 降噪模块自适应滤波器进行建模并仿真。在建模过程中为了确保噪声的相关性,首先让噪声通过了一个低通FIR 滤波器,然后再将其与标准音频信号混合输入到LMS 自适应滤波器中,MATLAB/Simulink 仿真模型中标准音频信号采用频率0.05Hz 的正弦波,噪声信号为随机信号。MATLAB/Simulink 仿真模型如图2 所示。将噪声信号及音频信号输入到数字降噪自适应滤波器之后将产生输出信号和降噪信号,输出信号为自适应的跟踪音频信号,而降噪信号就可以把环境中的噪声信号抵消掉,人的耳朵接收到的信号则变成较纯净的音频信号。
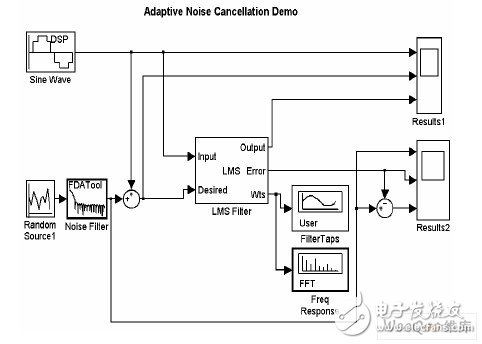
图 2 Simulink 中自适应滤波器仿真
让Simulink 仿真模型运行后,显示结果如图3 所示,通过仿真结果可知自适应滤波器在数字降噪技术应用中对噪声的消除效果非常好,通过自适应的调整滤波器参数,慢慢使降噪误差逐渐减小。表明了数字降噪技术比模拟降噪技术具有很大的优势,降噪效果更加明显。
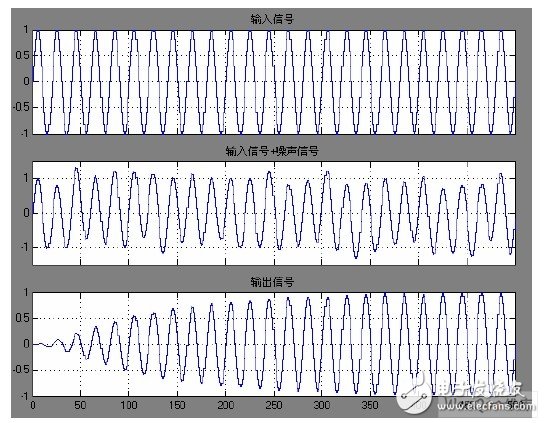
(a)输入信号与输出信号波形
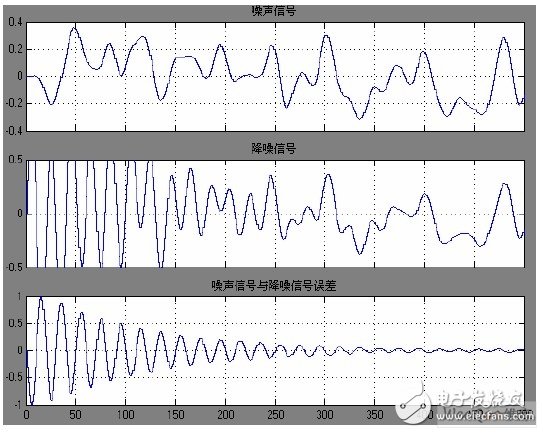
图3(b)噪声信号与降噪信号波形
5 数字降噪自适应滤波器的程序实现
在数字降噪技术研究中,一般用到数字信号处理器(DSP)进行开发研究,而在设计过程中将模型应用到DSP 之前,先将模型应用MATLAB 语言编写m 文件,然后再进一步转换成DSP 所需要的C 语言或汇编语言程序。本文分别给出了LMS 算法迭代运算部分的MATLAB语言m 文件程序及DSP 开发工具件visualdsp++中的LMS 算法C 序。MATLAB 语言m 文件LMS 算法部分程序:
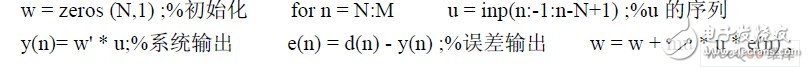

6 结论
本文论述了数字降噪技术比模拟降噪技术的优势以及数字降噪技术的典型应用数字降噪耳机的设计。文中简单介绍了数字降噪耳机降噪模块自适应滤波器设计的原理,自适应LMS 算法。并且利用MATLAB 中Simulink 工具建立了LMS 自适应噪声消除的模型,实现了数字降噪耳机DSP 降噪模块实现噪声消除功能的自适应滤波器的设计,对其进行了MATLAB 语言程序的编写以及C 预言程序的编写。仿真结果表明,此设计达到了很好的效果,后期可以实现了数字降噪耳机的功能设计,弥补了模拟降噪耳机设计中的不足,使降噪技术的发展又上了一个新的台阶。
-
基于DSP的自适应滤波器的设计方案2013-11-05 8896
-
基于AccelDSP的自适应滤波器设计2010-04-24 0
-
基于小波分析的自适应滤波器模型2017-03-02 0
-
自适应滤波器2017-08-14 0
-
如何去设计子带分解的自适应滤波器?2021-05-07 0
-
LabVIEW开发自适应降噪ANC2023-11-30 0
-
基于自适应滤波器的系统识别研究与实现2009-07-11 688
-
自适应数字滤波器课件PPT2009-07-25 875
-
自适应IIR滤波器设计策略研究2009-08-06 607
-
子带分解的自适应滤波器的FPGA实现2011-01-18 1525
-
自适应滤波器原理2016-07-20 1289
-
自适应滤波器的作用、原理以及相关应用2017-11-27 22084
-
图像处理基础自适应中值滤波器(基于OpenCV实现)2018-03-05 11746
-
LMS自适应滤波器的算法原理和应该如何实现2020-10-20 1749
-
自适应滤波器基本概念2021-10-25 4787
全部0条评论

快来发表一下你的评论吧 !

