新型分形天线加载的Sierpinski垫片天线介绍

射频识别（Radio Frequency Identification，RFID）是20世纪90年代兴起的一项自动识别技术。该技术利用无接触方式获取目标信息，并与目标信息进行双向通信。由 于其无接触的工作特性，它被称为第三代自动识别技术。一个自动识别系统有两个部分组成：读写器和电子标签。天线在读写器和电子标签中间担当着十分重要的作 用，它是两者之间实现非接触双向通信必不可少的器件。天线被用来发射和接收信号，并且担当着电子标签芯片中耦合能量的重要作用。所以电子标签天线设计的好 坏直接影响着系统的工作距离以及使用范围。

在RFID系统应用中，电子标签天线需要附着在需要识别的物体上，作为识别物品的身份象征，并且由于被识别物体的多样性，人们对电子标签天线提出了更高的 要求，主要体现在宽频带、小型化、便于安装和携带，同时要求天线有高的效率。天线设计很大程度依赖天线的频率，有些类型的天线具有很宽的带宽，如螺旋天 线。这种天线从某种意义上来说是分形天线的自相似性具体化，分形天线的自相似性对于电子标签天线的设计具有具有重要意义。

分形天线是一种新型天线，它将分形几何应用于天线，完全不同于传统意义上的欧式几何天线。分形结构的高度空间自填充特性可以转变为分形天线的小型化特征， 例如Koch分形天线、Hilbert分形天线、Minkinski分形天线等。分形结构的自相似性可以转变为分形天线的多频段特性，典型的有 Sierpinski分形天线。

本文提出了一种新型分形天线加载的Sierpinski垫片天线，与传统天线相比，此天线充分利用了新型分形结构的高度自填充性以及Sierpinski分形天线的的多频段特性，从而实现了一种新型的小型化、多频段分形天线。

1 分形结构的几何描述和天线生成

分形结构的天线构造形式很多，本文采用两点格式法进行构造新型分形天线。先定义一个初始元和一个生成元，初始元给定了分形图形的框架，生成元给定了新型分形天线的构造方法。此新型分形天线的初始元和生成元如图1所示。

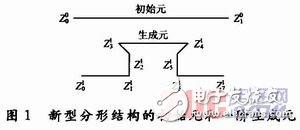
图1中符号的上标代表迭代次数，下标代表坐标点。选取：

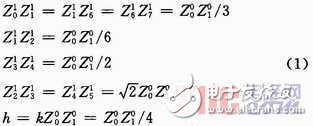
式中：k=1／4为分形凹入的宽度。

由分形理论可以知道，该新型分型结构的分形维数D取决于以下方程：

　　

通过1阶生成元的迭代过程，可以进行再次迭代得到2阶及3阶生成元。虽然此新型分形曲线具有与Koch分形结构相同的迭代特性以及空间填充特性，但是分形 迭代在实际中不可能无限制的迭代下去，研究发现，此新型曲线在降低谐振频率上有一个极限值，一般在5阶以上性能就不明显了，这里称之为分形极限。同时，由 于现代制造工艺的限制，一般分型天线都在5阶以下。

此新型分形曲线同Koch分形曲线有很多相似之处，1阶新型分形曲线比1阶Koch曲线长30．18％，2阶新型分形曲线比同阶的Koch曲线长1．44 倍，而且具有分形天线的特性。由此可以说明，此分形天线具有比Koch分形结构更强的自填充能力，用在天线设计中可以实现更长的电流有效路径，从而降低谐 振频率，实现天线的小型化。

2 Sierpinski分形天线

Sierpinski三角形是由波兰数学家Sierpinski提出的一种分形结构，图2显示了使用迭代函数系统（IFS）构造Sierpinski分形天线的过程，它的分形维数为：D=In 3／In 2=1．58。

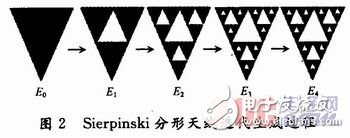
2．1 Sierpinski分形结构的边长对天线性能的影响

对于Sierpinski分形天线，这里研究了角度均为600，比例因子均为0．5时，三角形的边长分别为48 mm，56 mm，60 mm时，基于0阶和1阶的偶极子天线性能。天线结构如图3所示。利用HFSS 11．0进行仿真，其中1阶分形结构仅列出低频谐振频率，仿真结果如表1所示。

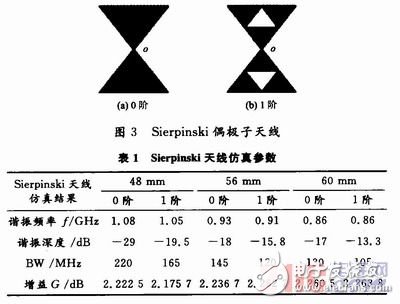
表1仿真结果表明：在天线比例因子不变，角度不变的条件下，随着边长的增长，谐振频率、谐振深度、带宽BW（VSWR《2）均在逐渐减小，这是由于 增益虽然变化不是十分明显，但是依然可以看出边长为60 mm时天线的增益最大，这有益于天线校正。总之，基于Sierpinski分形结构的天线的第一谐振频率与天线的周长和高度有关。在保持天线的周长和高度 不变的条件下，阶数的变化不会影响第一谐振频率点。

2．2 角度不同，对天线性能的影响

对于0阶Sierpinski分形天线而言，其实它就是两块三角形的平板，三角形板型天线为宽频带天线，这里研究当其两条边相同，但其所夹角不同时，天线 的性能。天线的边长为60 mm时，所夹角分别为30°，60°，90°，由HFSS 11．O仿真得其天线性能如表2所示。

从表2的仿真结果可以看出，角度为30°时，其天线的增益最大，同时，无论是角度大小，其谐振频率基本上是不变的。这是因为，对于Sierpinski垫片分天线而言，电流主要沿着三角形的两条边流动，而此时天线的边长都相等，所以谐振频率基本不变。

2．3 比例因子对天线性能的影响

文献中比较了张角θ=60°不变的条件下，比例因子δ分别为1．5和1．67对Sierpinski分形天线谐振频率的影响。结果表明随着比列因子δ的减 小，天线的谐振频率将向低频端移动。每种天线相邻谐振频率间的比率除第一个以外，均与其各自的比例因子值基本相同。谐振频率间的第一个比值相对偏大，这是 因为在天线的低频段，电流分布于整个天线表面，天线的终端效应比较强的缘故。研究表明Sierpinski分形天线迭代次数的增加，会出现多个谐振频率 点，且第一个谐振频率点与三角形的高度有关，辐射方向图与天线在空间的分布有关，而与天线的迭代次数没有关系。同时也给出，当角度减小到一定程度时，天线 的多频段特性均不明显。

3 新型分形加载的Sierpinski垫片天线

基于以上分析，设计出一款谐振在915 MHz新型加载Sierpinski垫片偶极子天线，此天线采用NXPG2XM标签芯片，其参数为在915 MHz时，芯片对外呈现阻抗为22-j195 Ω，天线的大小为96 mm×54 mm，它由顶角为60°的1阶Sierpinski分形和顶角为30°的0阶Sierpinski分形组成，在1阶Sierpinski分形天线的两边加 载新型分形天线，中间点为馈电点。天线模型如图4所示。

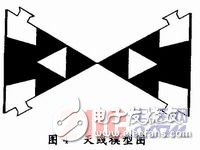
此天线利用新型分形加载Sierpinski天线，由于Sierpinski天线的电流主要沿着三角形的两条边流动，在三角形的两条边上加载新型分形天 线，有效延长了电流的有效路径，进而可以降低天线的谐振频率。同时，新型加载从另一个角度来说，在角度不变的条件下，使三角形的高度增加，有效延展天线电 流有效路径，减小了天线的大小。利用夹角为30°的0阶Sierpinski垫片天线高增益、宽频带特性，在谐振频段内实现了比较深的谐振深度，使得驻波 比更小。通过HFSS 11．O仿真，天线的增益方向图如图5所示，图6为回波损耗曲线及驻波比曲线。

从图5和图6中可以看出，在915 MHz，天线的谐振深度为-34 dB，其驻波比为1．05，天线的增益为2．28 dB，在VSWR《2时，带宽为190 MHz，相对带宽达到20．8％。在902～928 MHz时，天线的驻波比均在1．15以下。

在天线的设计中，新型分形天线的宽度对谐振深度的影响比较大，考虑到工业应用的要求以及谐振深度的因素，此天线的宽度为0．2～1 mm，同时，天线宽度的增大，也能微弱地降低谐振频率。天线的宽度做得过宽，对新型分形天线的迭代次数受到限制，正如前文所说，虽然理论上可以无限迭代， 但是一般在5阶以下，迭代次数再增加，影响将不明显。

高阶新型分形加载Sierpinski垫片天线，能极大地降低高频端的谐振频率。对2阶新型分形加载天线；甚至能将高频端的谐振频率降低3 GHz以上，同时保持天线的辐射方向图基本不变。实际中高阶分形天线的宽度应该在O．05～0．2 mm，这将严重影响低频端的谐振频率的谐振深度，尤其是第一谐振频率，但对高频端的谐振频率将产生很好的效果，使得更加小型化、多频段的天线得到实现。

4 结语

介绍了一款新型的分形天线，它比Koch分形具有更强的空间自填充能力，同时分析了Sierpinski垫片分形天线性能的影响因素：三角形的边长、角度 和比例因子。在此基础上，设计了一款新型分形加载的Sierpinski垫片天线，它充分利用了新型分形天线的空间填充能力，延长了 Sierpinski分形天线的电流有效路径，增大了谐振波长，从而降低谐振频率，减小天线的尺寸，达到了极深的谐振深度。在无线电设备要求日益小型化的 今天有着实际的价值。