基于频谱分析仪的平均功率测量讨论分析

平均是减小测量系统固有不确定度的一个最常用的方法。进行多次测量，对其结果求平均，可以减小测量随机性的影响。如今大部分测量仪器都具有平均功能，仪器通常不是直接输出含有噪声的结果，而是测量上百次，计算出平均值，把平均值作为结果输出。但是下文会描述：频谱分析仪中的功率平均有时会导致不正确的结果。

本文的试验会引用两家不同厂商的频谱分析仪的功率测量结果。但是本文的结论对任何使用“后处理平均方法”的频谱分析仪都适用。

第一个错误观点：对均方根功率求平均，可以得出跨度为零的轨迹（或其一部分）的平均功率。为了更好的驳斥这个观点，有必要先了解一下平均的数学定义。如公式1所示：MAVE是某个试验N次测量的平均值，其中Mi是每一次测量的结果。

在这个例子中，仪器A和仪器B的结果，可接受的差异在一定范围之内（比如±1dB），所有的测试都是在频率跨度为零ZS（zero span）的情况下测试的，这时频谱分析仪会在一个固定的频点，测量这个频点的功率随时间变化的关系。这里并不是刻意选择ZS模式的，其实平均问题在传统的频域扫描测试中也存在。

在两个例子中，都采用ZS模式测量零信道功率比ACPR（adjacent-channel-power-ratio）。对于现代采用数字中频滤波器的频谱分析仪而言，这种测量功能是必备的，可以在偏离载波中心不同频偏的频率点多次测量功率，而不需要重新调谐频谱分析仪的中心频率。

图1显示的是ZS模式下，一个GSM时隙脉冲信号。其中蓝色的曲线是脉冲的功率包络。这里测量的是“射频输出调制谱”，也就是所谓的ACPR测量。

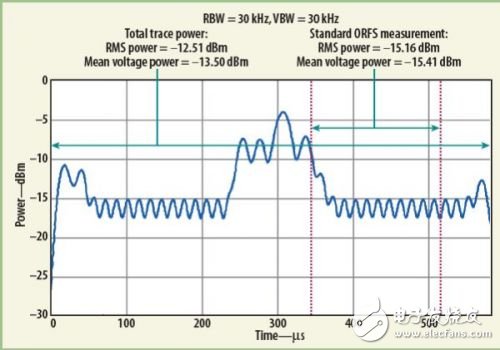
从这条曲线可以得到很多结果，如最大峰值功率、最小功率和平均功率，寻找最大/最小功率在概念上非常直观，仪器直接从轨迹中搜索出最大/最小点即可。

计算平均功率最简单的方法（当然也是正确的）就是对红色界限范围内的测量点求平均。如公式2所示，其中N是红色界限内的点数，Pith point是第i个点的功率。

问题是，仪器厂商对于功率平均的方法是不一致的。其中一个厂家是按照公式2来计算的；但是另一个厂商先把功率转换成电压，对电压求平均，再把平均电压换算成平均功率，如公式3所示。

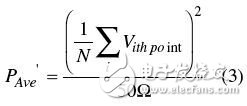
由于两种仪器输出的平均值的差别不大，所以很难看出其中一种仪器用的是公式2，而另一种用的是公式3。有必要从两种仪器分别取出多组轨迹，进行平均直到找到吻合之处。在图1的例子中，采用“真正的均方根”平均功率算法（后面简称RMS功率）的仪器，和采用“电压平均”功率的仪器之间的结果相差 0.25dB（前者比后者高0.25dB）。这点差异可能会被简单的认为是仪器之间的个体差异。尽管0.25dB看起来很小，但是当要求的精度仅仅是±1dB时，0.25dB就显得有点大了。如果是测量整个脉冲的平均功率的话（调制谱测量的是脉冲50%到90%时间内的功率），这个差异会扩大到约 1dB。这个值就会接近我们所要求的仪器之间误差容限了。

“电压平均”功率代表的是“先平均再平方（mean-squared）”的功率（如公式3），而“均方功率”则是“先平方再平均（mean- square）”功率。由统计学的知识我们可以得出：两者的差就是幅度变化。也就是说，两种仪器输出功率的差值就是幅度变化。而且“均方功率”永远大于 “电压平均功率”（RMS power 》 average voltage power）。

第二个关于功率平均的错误观点就是：对功率求平均总是在线形单位（瓦特）下进行的。实际上很多仪器常常采用对数平均。同样采用上面那个例子，假设测试中噪声影响很大，为了去除噪声，决定测量多组轨迹，对轨迹求平均。GSM标准规定，ORFS调制谱的测量需要对200个脉冲求平均。公式4是对应的计算公式，其中PTrace i是用公式2或公式3计算出的单条轨迹的平均值。

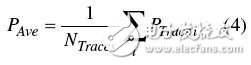
当然对这个功率的线性表达结果（单位为瓦特）求平均是合理的，但是很多仪器提供了对数平均功能。这个例子中，以dBm为单位的功率进行了平均。例如，求 1和 3dBm的平均值：如果用线性平均结果为：（1.25mW 2mW）/2=1.62mW= 2.11dBm；但是对数平均的结果为：（1dBm 3dBm）/2=2dBm。因此对数平均的结果会引入0.11dB的误差。

需要注意的是，对数平均引起的误差的大小和信号是否重复有关。尽管对数平均方法是错误的，但是对于重复信号，对数平均和线性平均的结果一致。需要注意，这里说的重复信号指的是每一个周期，其功率对时间关系是完全一样的。

必须要牢记：非重复信号会引入误差，如果不注意，经常会导致实验室的测量数据和实用环境中的误差很大。因为在实验室中，我们通常采用很好的“任意波形发生器ARB（arbitrary waveform generator）”作为信号源，这种源通常是把一个波形不断的重复播放。但是实用环境中的信号肯定不是重复性的。然而，只要不同周期之间的功率差别不是很大，对数平均和线性平均的误差也不会很大。

另一个需要注意的是，轨迹平均时，每次测得的各条轨迹之间对应的“点和点”的平均算法问题。同样的，信号的重复性会影响对数平均引起的误差。在这里，轨迹上的每一个点和其他轨迹上的对应点一起求平均，得出的结果作为这个点的平均值。

同样的，轨迹上的每一个点和其他轨迹上的对应点（同一个x轴）一起求平均，得出一条平均的轨迹线。这里x轴对应的是时间，当然对于频率也适用。和前面一样，这里可以采用线性平均或对数平均。这样对x轴上每一个点都做完平均之后就可以得到一条平均轨迹了。如果信号是重复的，线性平均和对数平均的结果相同，因为x轴上每一个点的功率在各次测量的轨迹上是相同的。

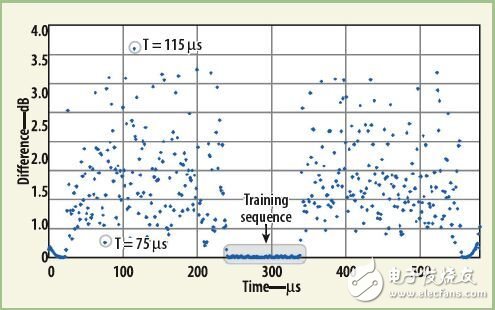
当被测信号不是重复的结果如何呢？图2就是对20个不同的EDGE信号，分别采用对数平均和线性平均后的结果。当然两条曲线会有差异，而且可以看出对数平均的结果比线性的小。图3显示的是两条曲线每一个点的差异。注意，正如我们所料，训练序列（译者注：用于同步和信道估计的部分，是完全重复的）部分的轨迹完全重合。

这些差异源于对数平均会放大功率的抖动，这个道理可以通过一个简单的例子描述：假设在某个特定的时间点（或者频点）反复测量N次功率值，功率在 0dBm和-10dBm之间抖动，其中一半的读数为0dBm，而另一半为-10dBm，即“峰-峰”差值为10dB。如果用对数平均，其结果为 -5dBm。但是如果用线性平均，要先把0dBm和-10dBm转为瓦特，然后求平均，最后再把瓦特转换为dBm，其结果是0.55毫瓦，即 -2.6dBm。因此采用对数平均的误差高达2.4dB。

众所周知，对数单位变化xdB，对应的线性功率变化为10（x/10）倍。因此可以用下面的公式得到正确值，假设一半的功率读数为Mhi，另一半的读数比刚才低ΔdB。

注意：随着Δ增加到无穷大，10log［（1 10-Δ/10）/2］这一项的数值趋向于-3dB。也就是说，如果两种功率出现的次数相等的时候，较高的功率最多比线性平均功率高3dB。还可以进一步把这个结果推广到任意的功率出现比例。

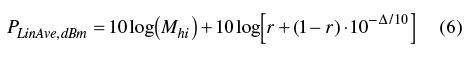
公式6中，r是高功率值（Mhi）出现的比例，当Δ趋向于无穷，平均功率最多比高功率小10log（r）倍。

当然，也可以推导出多数平均的结果

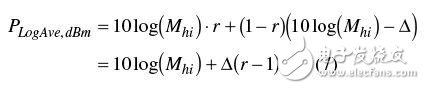
如果公式7减去公式6，其结果就是线性平均和对数平均的差异（即对数平均引入的误差）

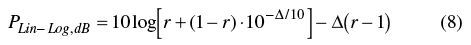
图4描述的是公式8的结果（对数平均的误差）随着Δ变化的关系，其中r是参变量。这张图的Δ只算到20dB，因为一般信号的峰均比都不会超过这个值。

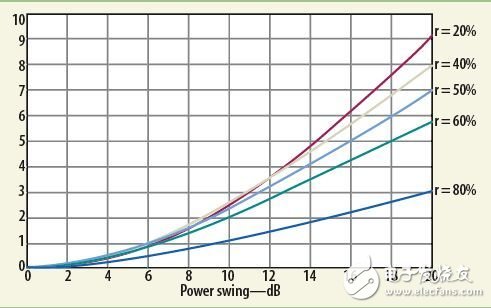
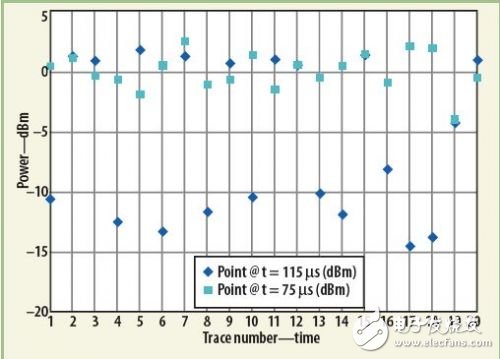
作为检验，有必要参考一下实际测试的数据（参见图3）。这幅图中有两个点被标出，一个是差异较大的点（差别大于3.5dB，T=115μs）），另一个是差异很小的点（约0.25dB，T=75μs）。根据前面的讨论，很容易理解在“功率对时间”的图形中，这些点的位置肯定不一样，误差大的点的摆幅比较大，而误差小的点的摆幅也相应的很小。这可以从图5中看出。

图5中，在T=115μs的这个点的摆幅高达约15dB，而在T=75μs的这个点，摆幅约5dB。假设高、低功率出现的次数相同（即 r=0.5），这T=115μs的这个点的摆幅约4.5dB，而T=75μs的这个点，摆幅约0.5dB（参见图4和公式8）。上述数字比实测的 3.5dB和0.25dB，要高一些，因为图4所示的是最坏情况（即只有两种功率读数，且出现机率相同），由于实际情况下，不止只有两种功率读数，所以实际结果要略小一些。

总而言之，工程师应该记住并不是所有的频谱分析仪输出的平均功率结果都是正确的。而且其误差的程度和被测信号有关，因此必须注意以下事项：

* 了解频谱分析仪计算平均功率的方法是RMS方法还是“电压平均”方法

* 功率应该在线性单位（瓦特）下进行平均，但是有些仪器会提供对数平均

* 重复信号对于理解对数平均的误差可能有误导作用。其结果要么是固定误差（例如RMS功率和电压平均功的误差为恒定值），要么就没有误差（例如对数平均和线性平均的结果相同）

不同的平均方法导致的误差可能到达1dB以上。理解仪器如何平均的的最好方法是，取出几条轨迹的数值，手工（编程）求其平均值，判断仪器输出结果是否和手工计算的相同。尽管这项工作比较麻烦，但是对于高精度的功率测量来说，这个工作还是有必要的。