

idea加密算法及原理详解
编程语言及工具
描述
idea
IDEA 全称IntelliJ IDEA,是java语言开发的集成环境,IntelliJ在业界被公认为最好的java开发工具之一,尤其在智能代码助手、代码自动提示、重构、J2EE支持、Ant、JUnit、CVS整合、代码审查、 创新的GUI设计等方面的功能可以说是超常的。IDEA是JetBrains公司的产品,这家公司总部位于捷克共和国的首都布拉格,开发人员以严谨著称的东欧程序员为主。
IDEA加密算法简介
1、IDEA加密算法概述
IDEA加密算法是一个分组长度为64比特的分组密码算法,密钥长度为128比特,由8轮迭代操作实现。每个迭代都由三种函数:mod(216)加法、mod(216+1)乘法和逐位异或算法组成。整个算法包括子密钥产生、数据加密过程、数据解密过程三部分。该加密算法规定明文和密文块均为64比特,密钥长度为128比特,加解密相同,只是密钥各异。
(1)IDEA加密算法的加密过程
IDEA总共进行8轮迭代操作,每轮需要6个子密钥,另外还需要4个额外子密钥输出变换,所以总共需要52个子密钥,这52个子密钥都是从128比特密钥中扩展出来的。
输入的明文为8个字符(即64比特),将64比特数据块分成X1,X2,X3,X4四个子块,每一子块16比特。这4个子块将作为第一轮迭代的输入,全部共8轮迭代。在每一轮中,这4个子块相互异或、相加和相乘,且与6个16比特子密钥相异或、相加和相乘。最后在输出变换中4个子块与4个子密钥进行运算。加密过程如图1所示。
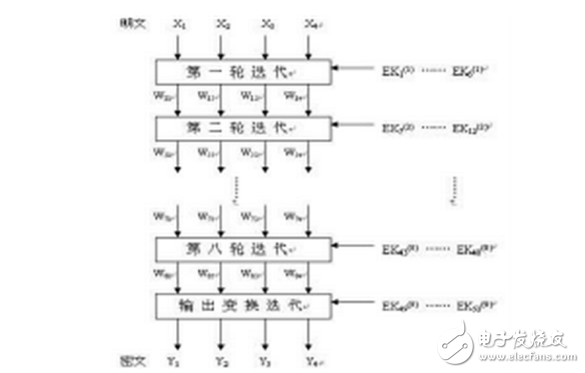
1、加密密钥扩展算法的实现
在IDEA加密算法中,实际上是将128比特密钥扩展为832比特。每一个字节用0补足16位。具体是如何扩展的呢?在前面的扩展思想中已经知道密钥串分8个子块,循环左移7次,其中第7次循环是取前4个,所以最终形成832比特(16*8*6+16*4)。扩展密钥数组为m_nKeyEncryptBox[52],部分代码如下:
byte[]asciiBytes=Encoding.Convert(unicode,ascii,unicode.GetBytes(this.m_sEncryptionKey));
//将一组字符编码成一个字节序列
char[]asciiChars=newchar[ascii.GetCharCount(asciiBytes,0,asciiBytes.Length)];
//进行字节到字符再到串的转换
ascii.GetChars(asciiBytes,0,asciiBytes.Length,asciiChars,0);
//由密钥m_sEncryptionKey扩展成加密密钥扩展数组m_nKeyEncryptBox
for(j=0;j《8;j++)//加密子密钥[j]循环左移8+[j+1]位
加密算法
是旅居瑞士中国青年学者来学嘉和著名密码专家J.Massey于1990年提出的。它在1990年正式公布并在以后得到增强。这种算法是在DES算法的基础上发展出来的,类似于三重DES,和DES一样IDEA也是属于对称密钥算法。发展IDEA也是因为感到DES具有密钥太短等缺点,已经过时。IDEA的密钥为128位,这么长的密钥在今后若干年内应该是安全的。
idea
类似于DES,IDEA算法也是一种数据块加密算法,它设计了一系列加密轮次,每轮加密都使用从完整的加密密钥中生成的一个子密钥。与DES的不同处在于,它采用软件实现和采用硬件实现同样快速。
由于IDEA是在美国之外提出并发展起来的,避开了美国法律上对加密技术的诸多限制,因此,有关IDEA算法和实现技术的书籍都可以自由出版和交流,可极大地促进IDEA的发展和完善
idea
IDEA曾今也是AES算法标准的主要竞争者,其安全性已经在国际密码年会上被证明。
在PGP(pretty good privacy)中,IDEA算法被采用。
64-位数据分组被分成4个16-位子分组:xl,X2,x3,x4。这4个子分组成为算法的第一轮的输入,总共有8轮。在每一轮中,这4个子分组相列相异或,相加,相乘,且与6个16-位子密钥相异或,相加,相乘。在轮与轮间,第二和第:个子分组交换。最后在输出变换中4个子分组与4个子密钥进行运算。
在每一轮中,执行的顺序如下:(以下表述中的相加指的是两个数mod 2^256 相加,例如:(a + b) mod p,其结果是a+b算术和除以p的余数,也就是说,(a+b) = kp +r,则 (a+b) mod p =r,又例如对于下列表述中的“(2)X2和第二个子密钥相加”就是指用X2与第二个子密钥的和除以2^16(即65536)后的余数。对于以下表述中的相乘,指的是:(a × b) mod p,其结果是 a × b算术乘法除以p的余数,又例如对于下列表述中的“(1)X1和第一个子密钥相乘。”就是指用X1和第一个子密钥相乘后的积除于(2^16+1)(即65537)后的余数。异或指的是不进位加法。)
(1)X1和第一个子密钥相乘。
(2)X2和第二个子密钥相加。
(3)X3和第三个子密钥相加。
(4)X4和第四个子密钥相乘。
(5)将第(1)步和第(3)步的结果相异或。·
(6)将第(2)步和第(4)步的结果相异或。
(7)将第(5)步的结果与第五个子密钥相乘。
(8)将第(6)步和第(7)步的结果相加。
(9)将第(8)步的结果与第六个子密钥相乘。
(10)将第(7)步和第(9)步的结果相加。
(11)将第(1)步和第(9)步的结果相异或。
(12)将第(3)步和第(9)步的结果相异或。
(13)将第(2)步和第(10)步的结果相异或。
(14)将第(4)步和第(10)步的结果相异或。
每一轮的输出是第(11)、(12)、(13)和(14) 步的结果形成的4个子分组。将中间两个分组分组交换(最后一轮除外)后,即为下一轮的输入。
经过8轮运算之后,有一个最终的输出变换:
(1) X1和第一个子密钥相乘。
(2) X2和第二个子密钥相加。
(3) X3和第三个子密钥相加。
(4) X4和第四个子密钥相乘。
最后,这4个子分组重新连接到一起产生密文。
产生子密钥也很容易。这个算法用了52个子密钥(8轮中的每一轮需要6个,其他4个用与输出变换)。首先,将128-位密钥分成8个16-位子密钥。这些是算法的第一批8个子密钥(第一轮六个,第二轮的头两个)。然后,密钥向左环移25位后再分成8个子密钥。开始4个用在第二轮,后面4个用在第三轮。密钥再次向左环移25位产生另外8个子密钥,如此进行D算法结束。
解密过程基本上一样,只是子密钥需要求逆且有些微小差别,解密子密钥要么是加密子密钥的加法逆要么是乘法逆。(对IDEA而言,对于模256十1乘,全0子分组用256=-l来表示,因此0的乘法逆是0)。计算子密钥要花点时间,但对每一个解密密钥,只需做一次。
关于IDEA中运用的很多概念,需要参考数论中的知识,如有疑问,可以参考以下资料:计算机密码学(卢开澄著清华大学出版社出版),计算机密码学及其应用,初等数论,数论导引(华罗庚著)等。关于IDEA运用的数学原理,均可在以上资料中获得答案。
-
加密算法的应用2025-10-24 183
-
加密算法的选择对于加密安全有多重要?2024-12-17 775
-
浅谈对称加密算法与非对称密钥加密算法2021-12-23 2149
-
Go常用的加密算法详细解读2021-09-01 3599
-
对称加密算法是什么2021-07-22 1714
-
uid加密算法2021-07-19 2746
-
举例几种常见的加密算法2021-04-28 21657
-
如何去实现DES加密算法?2021-04-26 1874
-
关于几种常用加密算法比较2018-03-19 6430
-
常见公钥加密算法有哪些2017-12-10 44867
-
c语言如何实现idea算法2017-12-08 8556
-
labview md5加密算法.llb2016-05-25 2904
-
汽车遥控加密算法2016-02-17 9103
-
采用多种加密算法的文件加密方法2011-05-26 873
全部0条评论

快来发表一下你的评论吧 !

