哈夫曼树带权路径长度怎么计算

　　哈夫曼树的带权路径长度是什么？

　　1．树的路径长度

　　树的路径长度是从树根到树中每一结点的路径长度之和。在结点数目相同的二叉树中，完全二叉树的路径长度最短。

　　2．树的带权路径长度（Weighted Path Length of Tree，简记为WPL）

　　结点的权：在一些应用中，赋予树中结点的一个有某种意义的实数。

　　结点的带权路径长度：结点到树根之间的路径长度与该结点上权的乘积。

　　树的带权路径长度（Weighted Path Length of Tree）：定义为树中所有叶结点的带权路径长度之和，通常记为：

　　其中：

　　n表示叶子结点的数目

　　wi和li分别表示叶结点ki的权值和根到结点ki之间的路径长度。

　　树的带权路径长度亦称为树的代价。

　　3．最优二叉树或哈夫曼树

　　在权为wl，w2，…，wn的n个叶子所构成的所有二叉树中，带权路径长度最小（即代价最小）的二叉树称为最优二叉树或哈夫曼树。

　　【例】给定4个叶子结点a，b，c和d，分别带权7，5，2和4.构造如下图所示的三棵二叉树（还有许多棵），它们的带权路径长度分别为：

　　（a）WPL=7*2+5*2+2*2+4*2=36

　　（b）WPL=7*3+5*3+2*1+4*2=46

　　（c）WPL=7*1+5*2+2*3+4*3=35

　　其中（c）树的WPL最小，可以验证，它就是哈夫曼树。

　　注意：

　　① 叶子上的权值均相同时，完全二叉树一定是最优二叉树，否则完全二叉树不一定是最优二叉树。

　　② 最优二叉树中，权越大的叶子离根越近。

　　③ 最优二叉树的形态不唯一，WPL最小

　　怎么求哈夫曼的带权路径长度

　　【问题描述】

　　已知输入两行正整数，第二行正整数之间用空格键分开，请建立一个哈夫曼树，以输入的数字为叶节点，求这棵哈夫曼树的带权路径长度。

　　【输入形式】

　　首先第一行为输入正整数的个数，然后接下来的一行正整数，代表叶结点，正整数个数不超过1000个

　　【输出形式】

　　输出相应的权值

　　【样例输入】

　　5

　　4 5 6 7 8

　　【样例输出】

　　69

　　关于哈夫曼树——

　　1、 路径长度

　　从树中一个结点到另一个结点之间的分支构成两个结点之间的路径，路径上的分支数目称做路径长度。

　　

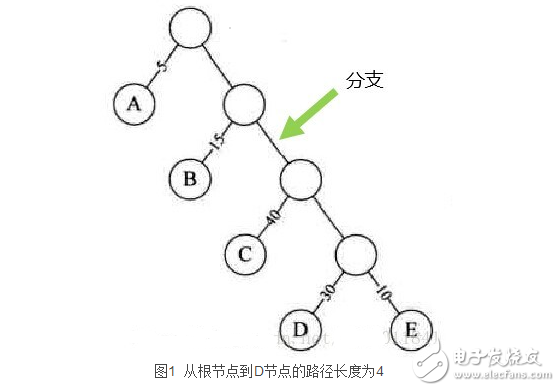
　　1、 树的路径长度

　　路径长度就是从树根到每一结点的路径长度之和。

　　

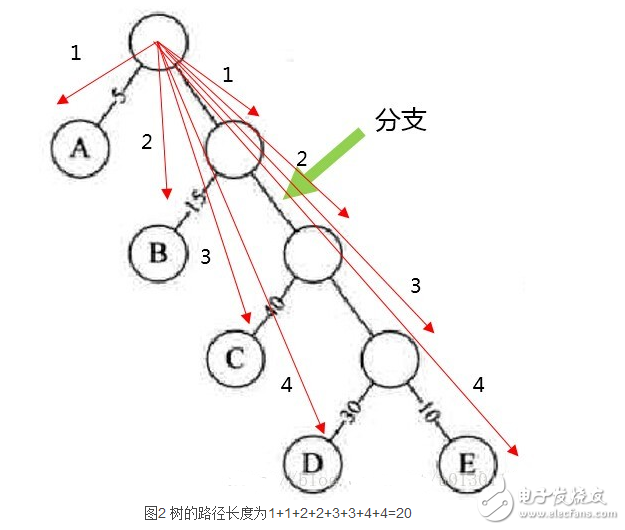
　　1、 哈夫曼树：

　　带权路径长度WPL（Weighted Path Length）最小的二叉树，也称为最优二又树。

　　例： 上图的WPL=1*5 + 2*15 + 3*40 + 4*30 + 4*10= 315

　　先了解通过刚才的步骤，我们可以得出构造哈夫曼树的算法描述。

　　1、根据给定的n个权值{w［1］，w［2］，…，w［n］}构成n棵二叉树的集合F={T［1］，T［2］，…T［n］}， 其中每棵二叉树T［i］;中只有一个带权为w［i］的根结点，其左右子树均为空。

　　2、在F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的。二叉树，且置新的二叉树的根结点的权值为其左右子树上根结点的权值之和，

　　3、在F中删除这两棵树，同时将新得到的二义树加入F中。

　　4重复2和3步骤，直到F只含一棵树为止。这棵树便是哈夫曼树。

　　结合例题说明一下这个算法

　

　　

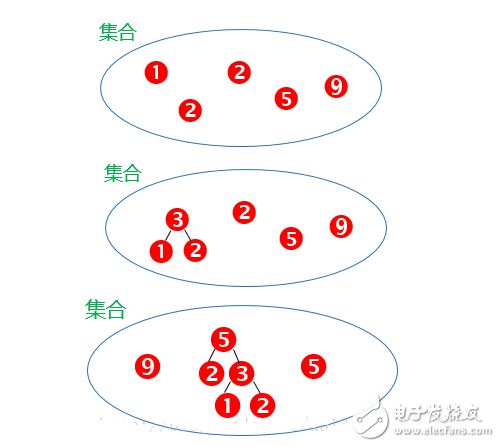
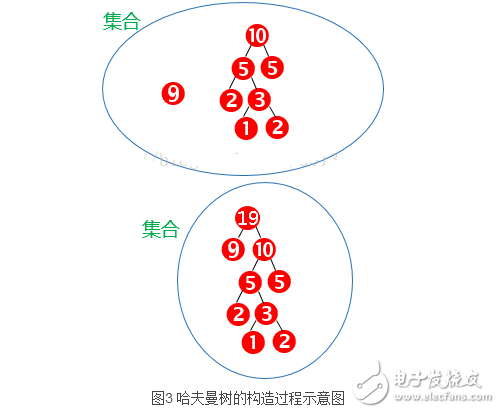
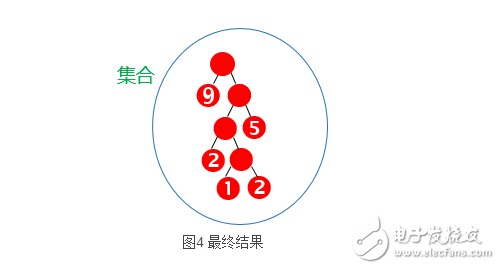
　　那么可以由上面的哈夫曼树计算出最小带权路径长度

　　WPL = 1*9 + 2*5 + 3*2 + 4*1 + 4*2 =37

　　另外还可以有另外一个方法，结合算法描述仔细观察发现最小带权路径长度为非叶子结点的和 ，即

　　WPL= 19 + 10 +5 +3=37

　　至于算法的正确性，一下子也想不到什么好的办法来证明，不过应该是可以逻辑推导过来的。

　　那么要实现这段程序，由上面的算法描述图我们已经知道差不多了，主要分为三步：

　　一、排序，直到数组中只有一个数则退出

　　二、最小两个数加起来，即为非叶子节点，累加到累加器中

　　三、把最小两个数加起来作为一个新的值保存在数组中，去掉最小两个值，跳回第一步

　　#include《stdio.h》

　　#include《stdlib.h》 //qsort（）;

　　#define N 1010

　　int rising（const void *a， const void *b）

　　{

　　return *（int*）a - *（int*）b;

　　}

　　int main（）

　　{

　　int leaf［N］ = {0}， n， i， sum = 0;

　　scanf（“%d”， &n）;

　　for（i=0; i《n; i++）

　　scanf（“%d”， leaf+i）;

　　for（i=0; i《n-1; i++）

　　{

　　qsort（leaf+i， n-i， sizeof（leaf［0］）， rising）; //排序并剔除已使用的叶结点

　　leaf［i+1］ += leaf［i］; //合并两个最小的叶结点成一新的节点（放在leaf［i+1］中）

　　sum += leaf［i+1］; //总路径长 = 所有非叶结点之和

　　}

　　printf（“%d\n”， sum）;

　　return 0;

　　}