空间电压矢量svpwm控制原理解析

　　空间矢量脉宽调制（Space Vector Pulse Width Modulation） 是已被应用于变频器、UPS、无功补偿器等领域的新技术。近年来随着大型重工业行业的技术改造和更新工作的展开，对大功率、高质量变频器的需求与日俱增，这种情况在我国尤其突出。电力电子技术、微电子技术和控制理论的发展，为变频器技术日趋成熟准备了条件，先进的SVPWM技术在此环境下应运而生。变频器的SVPWM算法与其拓扑结构有着密切的联系，因此必须根据变频器拓扑结构的不同，选取相应的控制算法。

　　SVPWM是近年发展的一种比较新颖的控制方法，是由三相功率逆变器的六个功率开关元件组成的特定开关模式产生的脉宽调制波，能够使输出电流波形尽可能接近于理想的正弦波形。空间电压矢量PWM与传统的正弦PWM不同，它是从三相输出电压的整体效果出发，着眼于如何使电机获得理想圆形磁链轨迹。SVPWM技术与SPWM相比较，绕组电流波形的谐波成分小，使得电机转矩脉动降低，旋转磁场更逼近圆形，而且使直流母线电压的利用率有了很大提高，且更易于实现数字化。

　　PAM是英文PulseAmplitudeModulation（脉冲幅度调制）缩写，是按一定规律改变脉冲列的脉冲幅度，以调节输出量值和波形的一种调制方式SPWM，就是在PWM的基础上改变了调制脉冲方式，脉冲宽度时间占空比按正弦规率排列，这样输出波形经过适当的滤波可。

　　SVPWM 基本原理

　　SVPWM 的理论基础是平均值等效原理，即在一个开关周期内通过对基本电压矢量加以组合，使其平均值与给定电压矢量相等。在某个时刻，电压矢量旋转到某个区域中，可由组成这个区域的两个相邻的非零矢量和零矢量在时间上的不同组合来得到。两个矢量的作用时间在一个采样周期内分多次施加，从而控制各个电压矢量的作用时间，使电压空间矢量接近按圆轨迹旋转，通过逆变器的不同开关状态所产生的实际磁通去逼近理想磁通圆，并由两者的比较结果来决定逆变器的开关状态，从而形成PWM 波形。逆变电路如图1-1示。

　　设直流母线侧电压为Uas，逆变器输出的三相相电压为UA，Ug ，Uc，其分别加在空间上互差1200 的三相平面静止坐标系上，可以定义三个电压空间矢量UA（t）.Ug（t）.Uc（t），它们的方向始终在各相的轴线上，而大小则随时间按正弦规律做变化，时间相位互差120。

　　假设Um为相电压有效值，f为电源频率，则有：

　

　　可见U（t）是一个旋转的空间矢量，它的幅值为相电压峰值的1.5倍，Um为相电压峰值，且以角频率c=2nf按逆时针方向匀速旋转的空间矢量，而空间矢量U（t）在三相坐标轴（a，b，c）上的投影就是对称的三相正弦量。

　

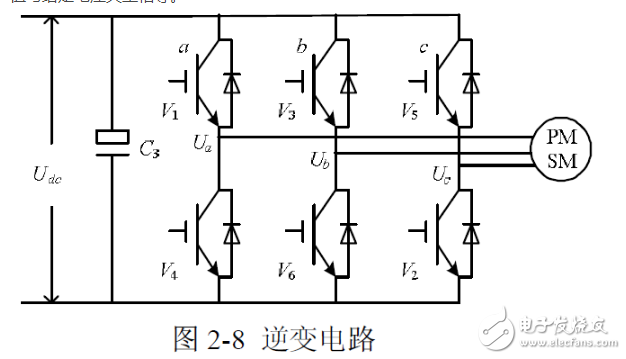
　　由于逆变器三相桥臂共有6 个开关管，为了研究各相上下桥臂不同开关组合时逆变器输出的空间电压矢量，特定义开关函数Sx（x= a，b，c）为：

　　

　　（Sa.Sb.Se）的全部可能组合共有八个，包括6 个非零矢量U1：（001）.U2：（010）.U3（011）.U4（100）.U5（101）.U6（110）。和两个零矢量Uo（000）.U7（111），下面以其中一种开关组合为例分析，假设Sx（x= a，b，c）= （100），此时

　

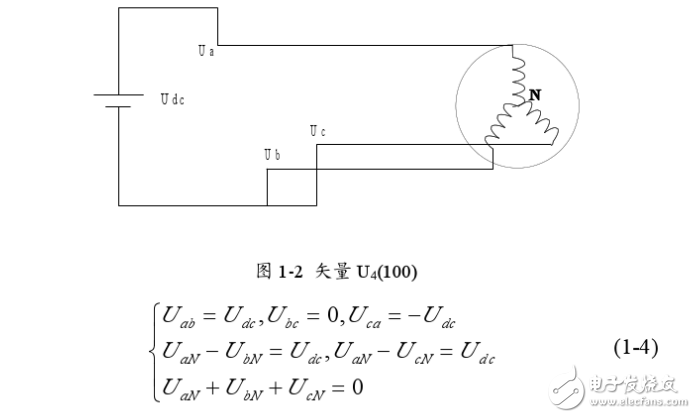
　　求解上述方程可得： Uan=2Uj/3、Ubn=-Ua/3、Ucn=-Ua /3。同理可计算出其它各种组合下的空间电压矢量，列表如下：

　　

　　

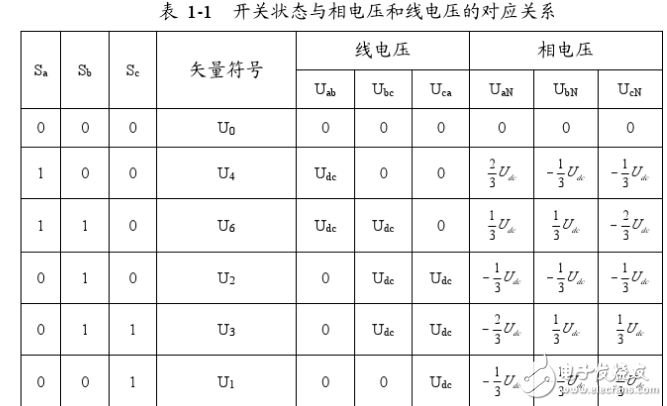
　　其中非零矢量的幅值相同（模长为2Ua/3），相邻的矢量间隔60*，而两个零矢量幅值为零，位于中心。在每一个扇区，选择相邻的两个电压矢量以及零矢量，按照伏秒平衡的原则来合成每个扇区内的任意电压矢量，即：

　

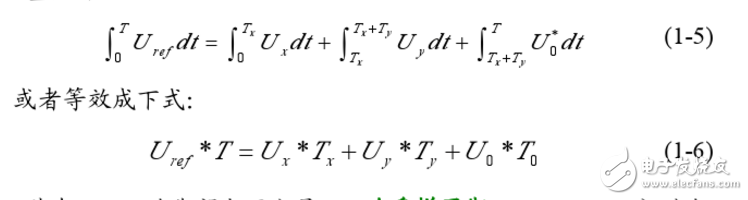
　　其中，Uref 为期望电压矢量; T 为采样周期; Tx，Ty、TO分别为对应两个非零电压矢量Ux.Uy和零电压矢量UO在一个采样周期的作用时间; 其中UO 包括了UO和U）两个零矢量。式（1-6）的意义是，矢量Uref 在T 时间内所产生的积分效果值和UX、Uy、UO分别在时间Tz.Ty.To 内产生的积分效果相加总和值相同。

　　由于三相正弦波电压在电压空间向量中合成一个等效的旋转电压，其旋转速度是输入电源角频率，等效旋转电压的轨迹将是如图1-3 所示的圆形。所以要产生三相正弦波电压，可以利用以上电压向量合成的技术，在电压空间向量上，将设定的电压向量由U4（100）位置开始，每一次增加一个小增量，每一个小增量设定电压向量可以用该区中相邻的两个基本非零向量与零电压向量予以合成，如此所得到的设定电压向量就等效于一个在电压空间向量平面上平滑旋转的电压空间向量，从而达到电压空间向量脉宽调制的目的。

　　SVPWM算法

　　三相电压给定所合成的电压向量旋转角速度为ω=2πf，则旋转一周所需的时间为T=1/ f；若载波频率是 fs ，则频率比为 R=fs / f。这样将电压旋转平面等切割成R个小增量，亦即设定电压向量每次增量的角度是：γ=2π/ R。

　　现在假设需要输出一个空间矢量Uref，假设它在第I扇区，我们先把第I扇区单独取出来，然后用和它相邻的两个电压空间矢量来表示它：

　　

　　得到以 U4、U6、U7 及 U0 合成的 Uref 的时间后，接下来就是如何产生实际的脉宽调制波形。在 SVPWM 调制方案中，零矢量的选择是最具灵活性的，适当选择零矢量，可最大限度地减少开关次数，尽可能避免在负载电流较大的时刻的开关动作，最大限度地减少开关损耗。因此，我们以减少开关次数为目标，将基本矢量作用顺序的分配原则选定为：在每次开关状态转换时，只改变其中一相的开关状态。并且对零矢量在时间上进行了平均分配，以使产生的 PWM 对称，从而有效地降低 PWM 的谐波分量。可以发现当 U4（100）切换至 U0（000）时，只需改变 A 相上下一对切换开关，若由 U4（100）切换至 U7（111）则需改变 B、C 相上下两对切换开关，增加了一倍的切换损失。因此要改变电压向量 U4（100）、U2（010）、U1（001）的大小，需配合零电压向量 U0（000），而要改变 U6（110）、U3（011）、U5（100）， 需配合零电压向量 U7（111）。这样通过在不同区间内安排不同的开关切换顺序， 就可以获得对称的输出波形，其它各扇区的开关切换顺序如表 2-2 所示。

　　

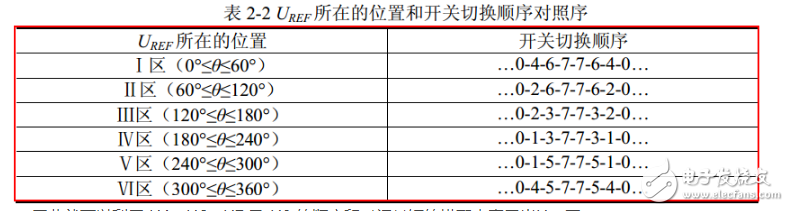
　　因此就可以利用 U4、U6、U7 及 U0 的顺序和时间长短的搭配来表示出Uref了。

　　以第Ⅰ扇区为例，其所产生的三相波调制波形在一个载波周期时间Ts 内如图 2-11 所示，图中电压向量出现的先后顺序为 U0、U4、U6、U7、U6、U4、U0，各电压向量的三相波形则与表 2-2 中的开关表示符号相对应。再下一个 载波周期Ts ，Uref 的角度增加一个γ，利用式（2-33）可以重新计算新的 T0、T4、T6 及 T7 值，得到新的类似图 2-11 的合成三相波形；这样每一个载波周期 TS 就会合成一个新的矢量，随着 θ 的逐渐增大，Uref 将依序进入第Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ区。在电压向量旋转一周期后，就会产生 R 个合成矢量。

　

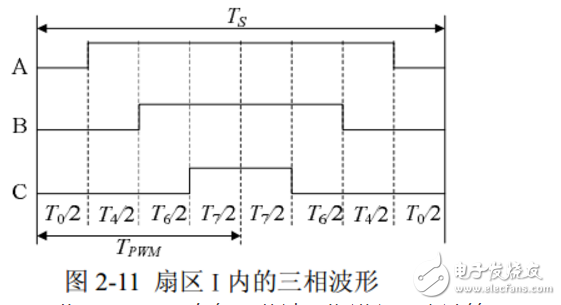
　　因此SVPWM会在每个载波周期进行一次计算。

　　通过以上 SVPWM 的法则推导分析可知要实现 SVPWM 信号的实时调制， 首先需要知道参考电压矢量 Uref 所在的区间位置，然后利用所在扇区的相邻两电压矢量和适当的零矢量来合成参考电压矢量。

　　控制系统需要输出的矢量电压信号 Uref，它以某一角频率 ω 在空间逆时针旋转，当旋转到矢量图的某个 60°扇区中时，系统计算该区间所需的基本电压空间矢量，并以此矢量所对应的状态去驱动功率开关元件动作。当控制矢量在空间旋转 360°后，逆变器就能输出一个周期的正弦波电压。

　　1.合成矢量Uref 所处扇区N 的判断

　　空间矢量调制的第一步是判断由Uα 和Uβ所决定的空间电压矢量所处的扇区。

　　假定合成的电压矢量落在第 I 扇区，可知其等价条件如下： 0《arctan（Uβ/ Uα） 《60

　　落在第 I 扇区的充分必要条件为：Ua 》 0 ，Uβ 》 0 且Uβ/Ua 《√3。

　　同理可得到合成的电压矢量落在其它扇区的等价条件，得出：

　　Uref落在第Ⅱ扇区的充要条件为：Ua》0 且Uβ/ Ua》√3；

　　Uref落在第Ⅲ扇区的充要条件为：Ua《0 ，Uβ》 0 且-Uβ/Ua 《√3；

　　Uref落在第Ⅳ扇区的充要条件为：Ua《0 ，Uβ 《 0 且Uβ/Ua 《√3；

　　Uref落在第Ⅴ扇区的充要条件为：Uβ《0 且 -Uβ/Ua》√3；

　　Uref落在第Ⅵ扇区的充要条件为：Ua》0 ，Uβ《0且-Uβ/Ua 《√3；

　　若进一步分析以上的条件，可看出参考电压矢量 Uref 所在的扇区完全由Uβ、√3Ua-Uβ、-√3Ua-Uβ三式决定，因此令：

　　

　　可以看出 A，B，C 之间共有八种组合，但由判断扇区的公式可知 A，B，C 不会同时为 1 或同时为 0，所以实际的组合是六种，A，B，C 组合取不同的值对应着不同的扇区，并且是一一对应的，因此完全可以由 A，B，C 的组合判断所在的扇区。为区别六种状态，令 N=4*C+2*B+A，则可以通过下表计算参考电压矢量 Uref所在的扇区。

　　

　　采用上述方法，只需经过简单的加减及逻辑运算即可确定所在的扇区，对于提高系统的响应速度和进行仿真都是很有意义的。

　　2.基本矢量作用时间计算与三相 PWM 波形的合成

　　在传统 SVPWM 算法如式（2-34）中用到了空间角度及三角函数，使得直接计算基本电压矢量作用时间变得十分困难。实际上，只要充分利用 Uα 和 Uβ 就可以使计算大为简化。

　　以 Uref 处在第Ⅰ扇区时进行分析，根据图 2-10 有：

　　

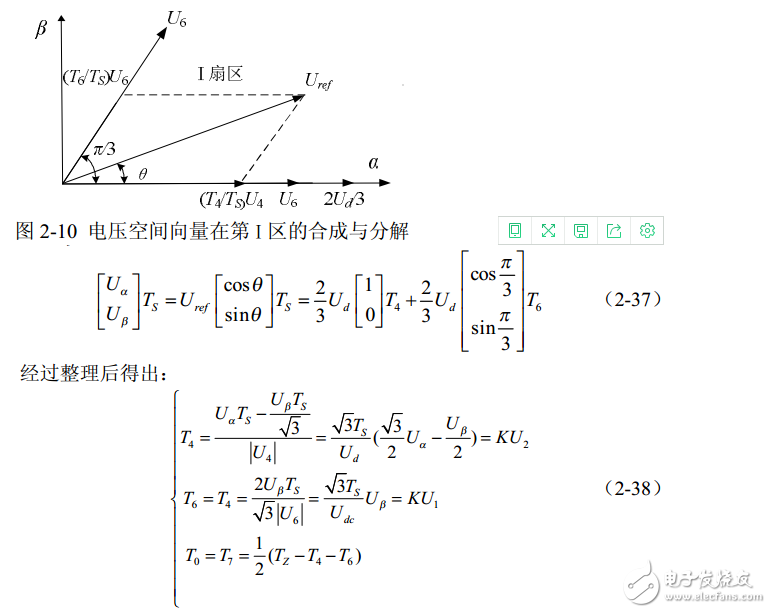
　　同理可求得Uref在其它扇区中各矢量的作用时间，结果如表2-4所示。表中两个非零矢量作用时间的比例系数为 K =3Ts/Udc 。由此可根据式2-36 中的U1 、U2、U3判断合成矢量所在扇区，然后查表得出两非零矢量的作用时间，最后得出三相PWM波占空比，表2-4可以使SVPWM算法编程简易实现。

　

　　由公式（2-38）可知，当两个零电压矢量作用时间为0时，一个PWM周期内非零电压矢量的作用时间最长，此时的合成空间电压矢量幅值最大，由下图2-12可知其幅值最大不会超过图中所示的正六边形边界。而当合成矢量落在该边界之外时，将发生过调制，逆变器输出电压波形将发生失真。在SVPWM调制模式下，逆变器能够输出的最大不失真圆形旋转电压矢量为图2-12所示虚线正六边形的内切圆，其幅值为： （√3/ 2）x（2Udc / 3） =√3Udc /3 。即逆变器输出的不失真最大正弦相电压幅值为√3Udc /3 ，而若采用三相SPWM调制，逆变器能输出的不失真 最大正弦相电压幅值为Udc/2。显然SVPWM 调制模式下对直流侧电压利用率更高，它们的直流利用率之比为（√3Udc / 3） /（Udc / 2） =1.1547 ，即SVPWM算法比SPWM算法的直流电压利用率提高了15.47%。

　

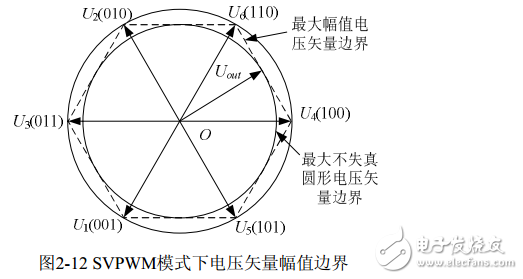
　　如图当合成电压矢量端点落在正六边形与外接圆之间时，已发生过调制，输出电压将发生失真，必须采取过调制处理，这里采用一种比例缩小算法。定义每个扇区中先发生的矢量用为 Tx，后发生的矢量为 Ty。当 Tx+Ty≤TS时，矢量端点在正六边形之内，不发生过调制；当 Tx+Ty》TS时，矢量端点超出正六边形，发生过调制。输出的波形会出现严重的失真，需采取以下措施：

　　设将电压矢量端点轨迹端点拉回至正六边形内切圆内时两非零矢量作用时间分别为 Tx‘，Ty’，则有比例关系：

　

　　推荐阅读：

　　svpwm与spwm的区别和联系

　　svpwm算法原理及分析