无功功率到底是什么_怎么理解

　　无功功率，许多用电设备均是根据电磁感应原理工作的，如配电变压器、电动机等，它们都是依靠建立交变磁场才能进行能量的转换和传递。为建立交变磁场和感应磁通而需要的电功率称为无功功率，因此，所谓的“无功”并不是“无用”的电功率，只不过它的功率并不转化为机械能、热能而已；因此在供用电系统中除了需要有功电源外，还需要无功电源，两者缺一不可。无功功率单位为乏（Var）。

　　根据电磁感应原理工作的，如配电变压器、电动机等，它们都是依靠建立交变磁场才能进行能量的转换和传递。为建立交变磁场和感应磁通而需要的电功率称为无功功率，因此，所谓的“无功”并不是“无用”的电功率，只不过它的功率并不转化为机械能、热能而已。

　　无功功率其实是一份真实的功率， 它的数量级和随伴它的有功功率一样，但被电路不停地吞吐着。虽则每半周期都抵消掉，基本上不消耗电能，但如果让它在电网中任意流动的话，它不但白占着电源的容量，而且增加了电网的损耗，加大电压降。

　　在交流输电中，无功功率是不可避免的。它在半周之内由零升到最大又降回零，电力系统要将如此巨大的一份电磁场能量，在半周之内吸收又放出来。使用的电流越大，建立的磁场能就越大，吞吐就越大。

　　1 无功功率的解析推演

　　要理顺无功功率的概念首先需对电力系统中的纯感性电路和纯容性电路分别进行简单的推演。 1.1 纯感性电路

　　

　　1.2 纯容性电路

　　

　　

　　

　　2 瞬时功率和平均功率推导

　　上述Um 和 I m 分别是正弦电压和正弦电流的幅值。为了接近实际，我们引入正弦电压和正弦电流的有效值（均方根值r.m.s.） 到式（5）和式（7）。

　　同时为方便计算，令电压作为参考（矢）量u = Um sin（ωt）。

　　

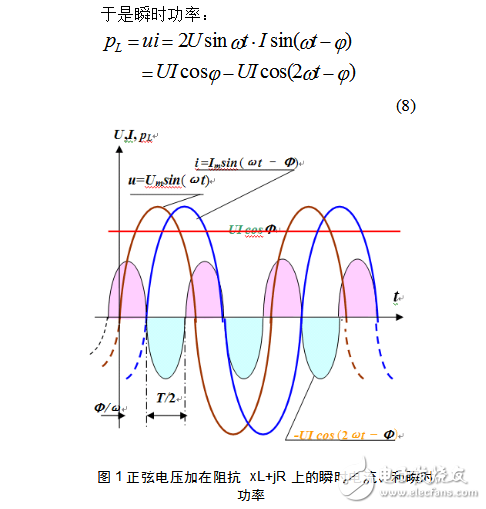
　　图1表示出瞬时电压u，瞬时电流，i和瞬时功率pL之间的关系。从（8）式看到，瞬时功率pL包括两部分：

　　恒定功率 p1 = UI cosφ= P （9）

　　和 交变部分p2 = UI cos（2ωt - φ） （10）

　　图1中 Φ/ω 是电流电压相差的时间表达式。 瞬时功率的交变部分p2是以两倍工频2ω变化。整个瞬时功率pL在一周期T 的平均功率：

　　

　　上式 （11） 、（12） 说明，消耗在电阻R平均功率，就是整个电路的平均功率。‘纯电感L’和‘纯电容C’都不消耗能量。

　　同时，瞬时功率交变部分p2可以进一步分解为：

　　2sin（sin）2cos（cos）

　　2cos（2tUItUItUIp

　　p2式的第一项是以平均功率P =UI cos φ为振

　　

　　3 复空间中的正弦交变量

　　3.1 旋转矢量

　　以上推算属于解析推演，是最基础的物理和数学方法，能准确地描述瞬时过程和对时间的平均值，是最易理解和可信的分析。但只限于实空间（实轴），无法在同一场面内反映相位的关系。复数就能帮助我们克服这个困难。

　　

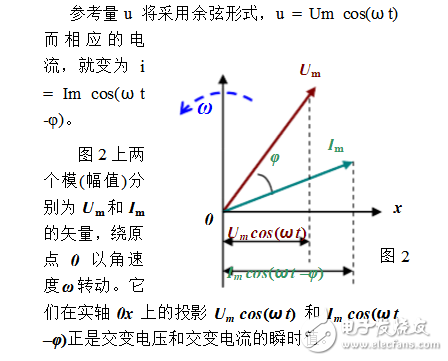
　　这些矢量，转动角速度 ω 是常数。所以，如果我们有一个以ω恒定转动的平面，相对于这样的平面，矢量变成固定的了。

　　以上的叙述还是基于实空间的，启示我们旋转矢量能代表正弦交变量。

　　3.2 旋转复平面

　　数的最普遍的形式是复数。它包含两个部分 —实部x和虚y。通常的实数或虚数，看成是复数的特殊情况。复数用复空间上一个矢量来表示。

　　

　　

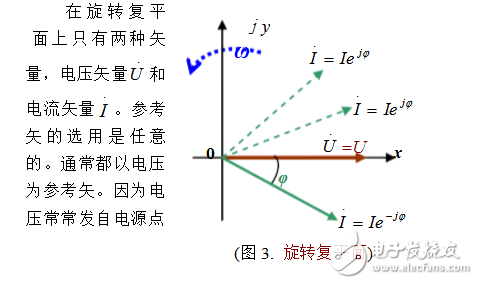
　　或在电路的始端。因此而驱动电流的相移相对这个始点是顺理成章的，如图3。

　　电能E， 功率 P， 无功功率 Q 和 阻抗 Z （包括电抗 xL ，xC ） 对旋转复平面，都是的标量。它们不能出现在旋转复平面。但它们可以以复数形式出现在静止的复平面上。

　　电压和电流是旋转复平面上的矢量。而它们的乘积（标量积），则是静止复平面上的矢量。

　　以感性电路为例，电流矢比电压矢滞后φ角度。

　　

　　4 结论

　　最后，我们回顾一下以上的基础推演和复平面推算的结论：

　　首先，由式（14）可见，瞬时功率的交变部分

　　

　　通过本文的理论分析和公式推演，我们可从不同的角度理清关于电力系统无功功率的一些模糊认识，其中的一些观点和结论可供电力系统相关工作人员加以参考和学习。