

matlab实现的自适应滤波算法
人工智能
描述
MATLAB语言简介
MATLAB是美国MathWorks公司开发的大型数学计算应用软件系统,它提供了强大的矩阵处理和绘图功能,简单易用,可信度高,灵活性好,因而在世界范围内被科学工作者、工程师以及大学生和研究生广泛使用,目前已经成为国际市场上科学研究和工程应用方面的主导软件。掌握MATLAB并借助它解决理论与应用问题已经成为每一个从事科学研究和工程技术人员应该具备的技能。
MATLAB是Matrix Laboratory(矩阵实验室)的缩写,是当前最流行、功能强大的科技应用软件和编程语言之一。MATLAB语言有以下特点:
1、功能强大:数值计算和符号计算,计算和编程可视化,数字和文字的统一处理,离线和在线计算;
2、界面友好,语言简明:以复数矩阵为计算单元,指令表达与数学表达式相近,是一种演算式语言;
3、开放性强:具有70余个功能强大的工具箱,覆盖面极广,可以完成数字图像处理、系统仿真、系统辨识、模糊控制、神经网络建模、信号处理、鲁棒控制、非线性控制、优化理论、统计分析等。
MATLAB成为应用学科计算机辅助分析、设计、仿真、教学必不可少的基础软件。工具箱函数为各个领域的研究和工程应用提供了有力的手段。
MATLAB系统的基本函数库具有初等函数、初等矩阵和矩阵变换、包括性代数方程组和矩阵特征值问题等数值线性代数、多项式运算和求根、数据析和傅立叶变换以及某些特殊的矩阵函数和数学函数等众多内容。
MATLAB还包括一系列被称作工具箱(TOOLBOX)的专业求解工具。工具箱实际上是MATLAB针对不同学科、不同专业所开发的专用函数库,用来求解各个领域的数值计算问题,包括数据采集工具箱、信号处理工具箱、图像处理工具箱、小波分析工具箱、控制工具箱等。随着MATLAB的不断升级,所含工具箱的功能越来越丰富,规模越来越庞大,因此,应用也越来越广泛,成为各种专业科研人员和工程技术人员的得力工具。
一个图形界面的完成,最终是通过图形界面的各种控件对象的操作来完成,而这些操作必定是通过Matlab 中函数代码的执行来完成的。函数代码的编制可以通过编写回调函数完成,而编写时当所要求执行的指令比较简单时,可以把该控件的代码直接写在“CallBack“属性中;当所要求执行的指令比较长时可以把函数代码放在一个自定义的M 文件中,在“CallBack”中直接将其文件名写上,也可以在主控文件中直接编写,当操作该控件时系统会自动执行“CallBack”中所要求执行的内容。
在本设计中,采用的是在主控文件中直接编写的方法,在GUI 界面单击当前需要编写程序的控件,然后右击将出现一个右键菜单,然后选择Callback 选项,即可直接进入主控M 文件,并且系统会自动生成语句。
目前的MATLAB已经成为国际上最为流行的软件之一,它除了传统的交互式编程之外,还提供了丰富可靠的矩阵运算、图形绘制、数据处理、图形处理,方便的windows编程等便利工具,出现了各种以MATLAB为基础的实用工具箱,广泛地应用于自动控制、图像信号处理、生物医学工程、语言处理、雷达工程、信号分析、振动理论、时序分析于建模、优化设计等领域。
算法实现设计
本课题的主要内容是在MATLAB上实现自适应滤波器的设计。课题的具体内容
为利用GUI界面设计出滤波器的选择界面、参数的输入界面、结果分析图等。其中滤波器的设计将会用两种算法实现既LMS算法和RLS算法,算法实现的基本设计框图如图4所示。
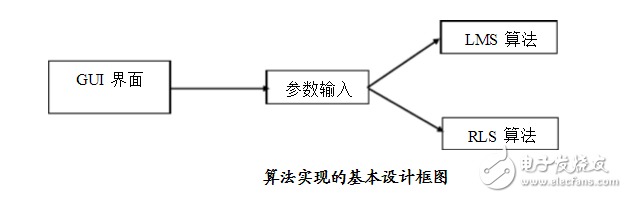
GUI界面的设计
由于本论文要实现两种不同的算法,通过GUI界面设计能给人一个比较好直观的效果。同时两种算法在参数取值方面会有不同之处,因此在软件设计中,我通过文本编辑框控件来接收用户输入的滤波器设计指标值,这让我们能更方便的通过调整不同的参数值观测实验结果,从而来保证滤波器的最佳状态。此外,Matlab 通过创建应用程序M 文件为GUI控制程序提供一个框架。所有代码都包含在应用程序M 文件中,即完成了图形界面的设计后,应用程序设计的主要工作是控件回调函数的设计。自适应滤波算法的主界面如图5。
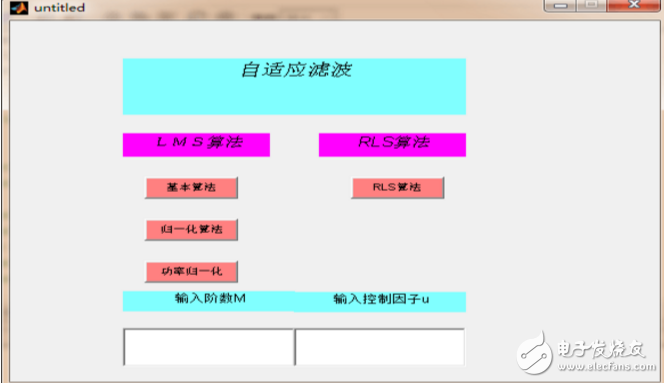
LMS算法的实现
LMS算法实现流程图如图6。
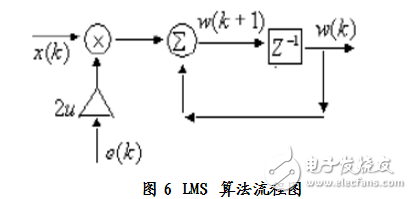
在图中,w(k)为滤波器滤波系数矢量估值,w(k+1)=w(k)-u,u是一个控制因子,用它来控制收敛速度与稳定性,u太大不稳定,u太小收敛速度很慢。通常0《u《1/max,max是R中的最大的特征值。(k)是误差梯度,直接计算(k)=J(w)/w很复杂,一般直接用误差的平方作为均方误差E|e(k)2估计值(k)。因为E{(k)}=k表明(k)是无偏估计。
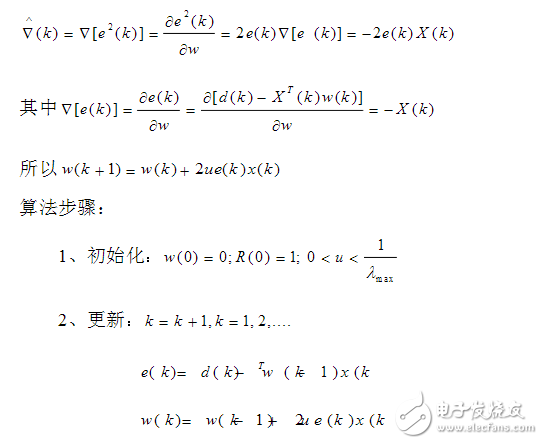
直到计算到达到(e)k预期小的值为止,或(w)k达到稳定为止。
根据u的取值不同LMS算法可分为以下三种类型:

方案1——基本的LMS算法的实现
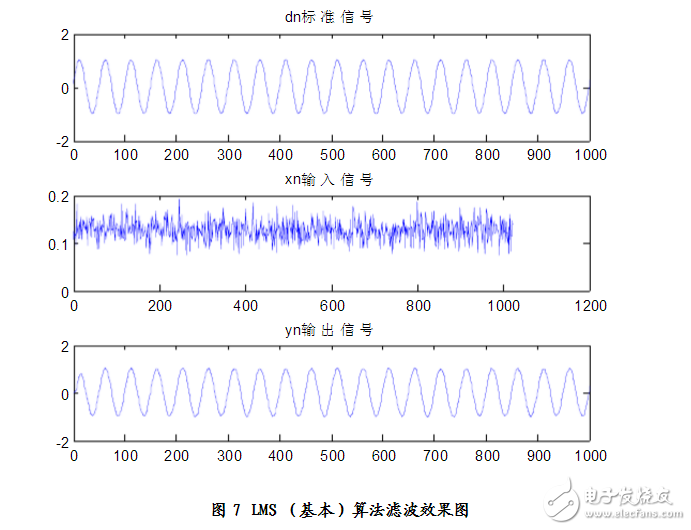
原信号与噪声信号相互独立,我们采用高斯白噪声作为噪声信号代替,并且定义噪声信号的功率为0.02,E((r(n))^2)=0.02,则v(n)=0.02*randn(1,1024)。基本的LMS算法要求控制因子u(k)为常数,所以在设计时我们得根据仿真结果来选择合适的u(k),以达到滤波器的最优滤波性能。为了完成输出信号与标准信号的对比,还必须定义一个标准信号,我们定义标准信号为正弦信号,这样方便我们更好的观测仿真数据。此外,定义w(n)为滤波器滤波系数矢量估值。最后,到了滤波器设计的关键阶段—算法的编程,我采用了for语句来实现算法的循环,直到计算到e(n)预期小的值为止或w(n)达到稳定为止。
算法编程如下:
for n=2:M
xn=sin(4*pi*n/100)+vn;
yn(n)=w1(n)*xn(n)+w2(n)*xn(n-1);
e(n)=xn(n)-yn(n);
w1(n+1)=w1(n)+2*u*e(n)*xn(n);
w2(n+1)=w2(n)+2*u*e(n)*xn(n-1);
end
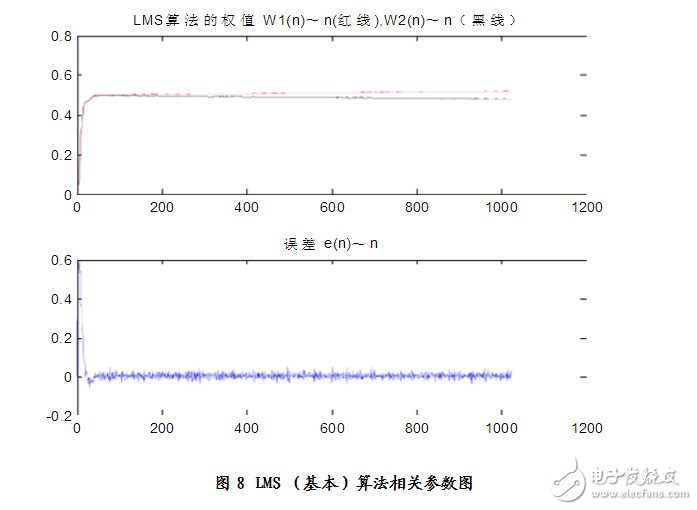
仿真结果:
见图7、图8 分析可得:n=20
Elapsed time is 0.094000 seconds.
方案2——归一化LMS算法的实现
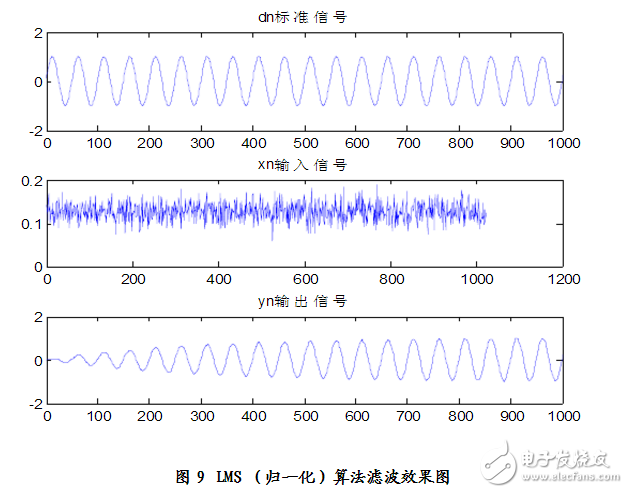
归一化算法与基本的LMS算法在思路上没有多大差别,就只是在对u(k)的选取方面有一定的差别,归一化中定义a(0,2),p》0因此,在for语句中需要对u(k)的取值加额外的要求。为了方便起见,我们暂且定义a=o,p=o
归一化LMS算法编程为:
for n=2:M
xn=sin(4*pi*n/100)+vn;
yn(n)=w1(n)*xn(n)+w2(n)*xn(n-1);
e(n)=xn(n)-yn(n); u(n)=1/(xn*xn‘);
w1(n+1)=w1(n)+2*u(n)*e(n)*xn(n);
w2(n+1)=w2(n)+2*u(n)*e(n)*xn(n-1);
end
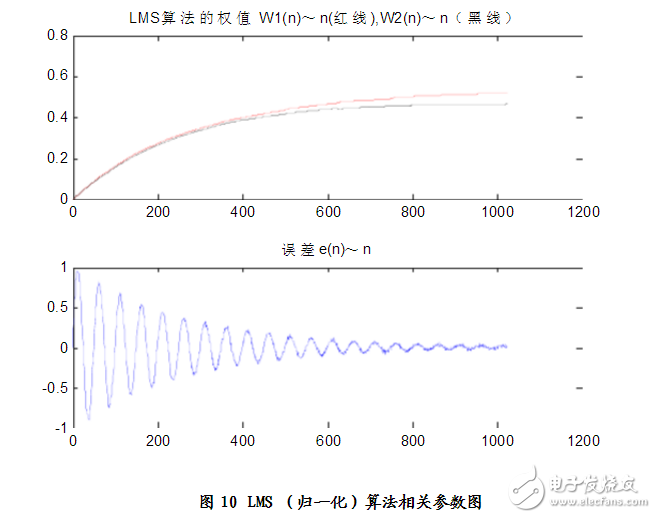
仿真结果:见图9、图10
分析可得:n=600
Elapsed time is 0.094000 seconds.
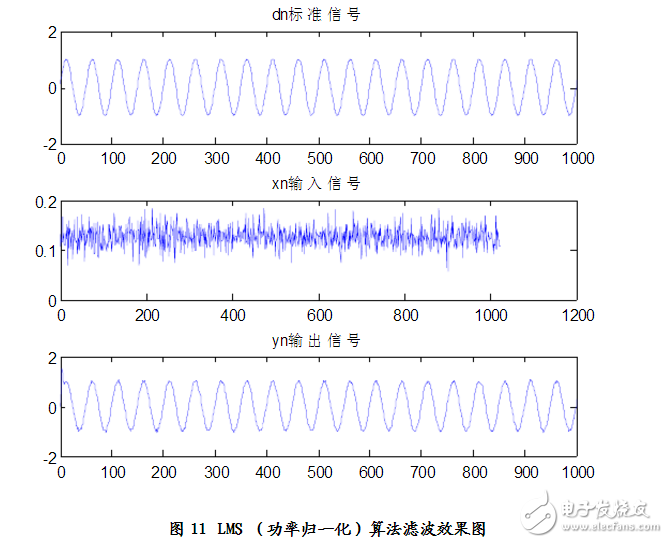
方案3——功率归一化LMS算法的实现
功率归一化,与归一化算法一样,也只是在对u(k)的取值方面有一定的差别。功率归一化中定义u(k)=a/g2x(k),其中g2x表示x(k)的方差。由a/g2x(k)=dg2x(k-1)+e2(k)可知,d《(0,1),0《a《2/m,其中M为滤波器的阶数。同时也为了方便起见,我们暂且定义a=1/M,d=0.5。
功率归一化LMS算法编程为:
for n=2:M
xn=sin(4*pi*n/100)+vn;
yn(n)=w1(n)*xn(n)+w2(n)*xn(n-1);
e(n)=xn(n)-yn(n);
gx2(n)=d*gx2(n-1)+e(n)*e(n); u(n)=a/(gx2(n));
w1(n+1)=w1(n)+2*u(n)*e(n)*xn(n);
w2(n+1)=w2(n)+2*u(n)*e(n)*xn(n-1);
end
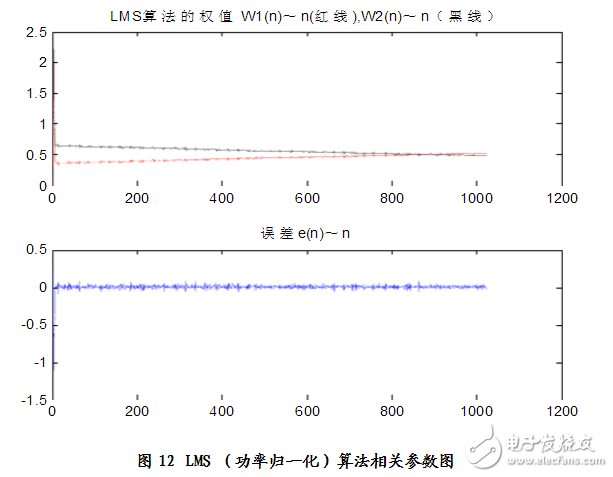
仿真结果:见图11、图12
分析得:n=8
Elapsed time is 0.078000 seconds.
LMS(least mean square)自适应滤波算法matlab实现
以下是matlab帮助文档中lms示例程序,应用在一个系统辨识的例子上。整个滤波的过程就两行,用红色标识。
x = randn(1,500); % Input to the filter
b = fir1(31,0.5); % FIR system to be identified
n = 0.1*randn(1,500); % Observation noise signal
d = filter(b,1,x)+n; % Desired signal
mu = 0.008; % LMS step size.
ha = adaptfilt.lms(32,mu);
[y,e] = filter(ha,x,d);
subplot(2,1,1); plot(1:500,[d;y;e]);
title(‘System Identification of an FIR Filter’);
legend(‘Desired’,‘Output’,‘Error’);
xlabel(‘Time Index’); ylabel(‘Signal Value’);
subplot(2,1,2); stem([b.‘,ha.coefficients.’]);
legend(‘Actual’,‘Estimated’);
xlabel(‘Coefficient #’); ylabel(‘Coefficient Value’);
grid on;
这实在看不出什么名堂,就学习目的而言,远不如自己写一个出来。整个滤波的过程用红色标识。
%% System Identification (SID)
% This demonstration illustrates the application of LMS adaptive filters to
% system identification (SID)。
%
% Author(s): X. Gumdy
% Copyright 2008 The Funtech, Inc.
%% 信号产生
clear all;
N = 1000 ;
x = 10 * randn(N,1); % 输入信号
b = fir1(31,0.5); % 待辨识系d
n = randn(N,1);
d = filter(b,1,x)+n; % 待辨识系统的加噪声输出
%% LMS 算法手工实现
sysorder = 32;
maxmu = 1 / (x‘*x / N * sysorder);% 通过估计tr(R)来计算mu的最大值
mu = maxmu / 10;
w = zeros ( sysorder , 1 ) ;
for n = sysorder : N
u = x(n-sysorder+1:n) ;
y(n)= w’ * u;
e(n) = d(n) - y(n) ;
w = w + mu * u * e(n) ;
end
y = y‘;
e = e’;
%% 画图
figure(1);
subplot(2,1,1); plot((1:N)‘,[d,y,e]);
title(’System Identification of an FIR Filter‘);
legend(’Desired‘,’Output‘,’Error‘);
xlabel(’Time Index‘); ylabel(’Signal Value‘);
subplot(2,1,2); stem([b’, w]);
legend(‘Actual’,‘Estimated’);
xlabel(‘Coefficient #’); ylabel(‘Coefficient Value’);
grid on;
-
归一化LMS算法自适应滤波器的MATLAB仿真与DSP实现2023-10-13 648
-
LMS自适应滤波器的MATLAB仿真和DSP实现2021-06-09 1597
-
如何实现基于四阶累积量的自适应均值滤波算法?2021-04-14 1827
-
LMS自适应滤波器的算法原理和应该如何实现2020-10-20 2035
-
自适应滤波算法与实现的PDF电子书免费下载2020-07-10 2965
-
自适应滤波算法理解与应用2017-12-14 27187
-
近期在做基于matlab的自适应FIR滤波器,主要是自适应算法的编程不会,请会的版主帮帮忙!!!2017-07-01 3628
-
自适应滤波算法2016-01-15 904
-
基于LMS算法与RLS算法的自适应滤波2012-07-06 2738
-
改进的LMS算法自适应滤波器的DSP实现2010-09-01 959
-
×字形滤波窗口在Matlab自适应中值滤波算法中的应用2010-07-08 3012
-
改进的变阶数LMS自适应滤波算法2010-05-13 3780
-
变步长LMS自适应滤波算法及其分析2010-04-26 3554
-
基于AccelDSP的自适应滤波器设计2010-04-24 3176
全部0条评论

快来发表一下你的评论吧 !

