蒙特卡洛模拟优缺点

　　蒙特卡罗模拟简介

　　蒙特·卡罗方法（Monte Carlo method），也称统计模拟方法，是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明，而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。与它对应的是确定性算法。蒙特·卡罗方法在金融工程学，宏观经济学，计算物理学（如粒子输运计算、量子热力学计算、空气动力学计算）等领域应用广泛。

　　蒙特卡罗模拟因摩纳哥著名的赌场而得名。它能够帮助人们从数学上表述物理、化学、工程、经济学以及环境动力学中一些非常复杂的相互作用。

　　数学家们称这种表述为“模式”，而当一种模式足够精确时， 他能产生与实际操作中对同一条件相同的反应。但蒙特卡罗模拟有一个危险的缺陷： 如果必须输入一个模式中的随机数并不像设想的那样是随机数， 而却构成一些微妙的非随机模式， 那么整个的模拟（及其预测结果）都可能是错的。

　　蒙特卡罗法优点：

　　1.方法的误差与问题的维数无关。

　　2.对于具有统计性质问题可以直接进行解决。

　　3.对于连续性的问题不必进行离散化处理

　　蒙特卡罗法缺点：

　　1.对于确定性问题需要转化成随机性问题。

　　2.误差是概率误差。

　　3.通常需要较多的计算步数N.

　　蒙特卡罗方法的缺点及其改进

　　我们知道，蒙特卡罗方法是非常好用来做积分的。如果要算一个函数f（x）在区间［a，b］内的积分，我们可通过计算机利用蒙特卡罗方法来计算出积分近似值。即先估计一个比f（x）在区间［a，b］内最大值还要大的c，（必须保证f（x）在区间［a，b］不小于0）然后不断地在二维矩形区域［a，b］×［0，c］内随机产生随机数对（e，f），判断f与f（e）的大小，并统计f《f（e）的数量n，当产生点的数量N足够大时，计算出n/N*（b-a）*c，这就是函数f（x）在区间［a，b］内的积分值。

　　对蒙特卡罗方法的改进：如果要算一个函数f（x）在区间［a，b］内的积分，令s=0，我们可以在区间［a，b］内产生N个随机数e，赋值：s+=f（e）/N（之所以这样做是为了防止溢出），当N足够大时，计算s*（b-a），这就是函数f（x）在区间［a，b］内的积分值。 改进方法的优点：

　　1.维度降低，节省一半产生随机数的时间，

　　2.相对精度更高，由于蒙特卡罗方法矩形上界需要估计，因此带来了一定的不确定性，估计值取得过大，显著提升计算时间，估计值取得过小，就会出现计算错误。而改进方法不需要估计！

　　3.改进方法可以求解蒙特卡罗方法所不能计算的积分，求解范围更大，如果积分函数f（x）在区间［a，b］内是无界的，或者积分函数f（x）在区间［a，b］内有负值，蒙特卡罗方法就无法求解。

　　蒙特卡罗模拟基本原理及思想

　　当所要求解的问题是某种事件出现的概率，或者是某个随机变量的期望值时，它们可以通过某种“试验”的方法，得到这种事件出现的频率，或者这个随机变数的平均值，并用它们作为问题的解。这就是蒙特卡罗方法的基本思想。蒙特卡罗方法通过抓住事物运动的几何数量和几何特征，利用数学方法来加以模拟，即进行一种数字模拟实验。它是以一个概率模型为基础，按照这个模型所描绘的过程，通过模拟实验的结果，作为问题的近似解。可以把蒙特卡罗解题归结为三个主要步骤：构造或描述概率过程；实现从已知概率分布抽样；建立各种估计量。

　　蒙特卡罗模拟的应用

　　通常蒙特卡罗模拟通过构造符合一定规则的随机数来解决数学上的各种问题。对于那些由于计算过于复杂而难以得到解析解或者根本没有解析解的问题，蒙特卡罗模拟是一种有效的求出数值解的方法。一般蒙特卡罗模拟在数学中最常见的应用就是蒙特卡罗积分。

　　蒙特卡罗算法表示采样越多，越近似最优解。举个例子，假如筐里有100个苹果，让我每次闭眼拿1个，挑出最大的。于是我随机拿1个，再随机拿1个跟它比，留下大的，再随机拿1个……我每拿一次，留下的苹果都至少不比上次的小。拿的次数越多，挑出的苹果就越大，但我除非拿100次，否则无法肯定挑出了最大的。这个挑苹果的算法，就属于蒙特卡罗算法。告诉我们样本容量足够大，则最接近所要求解的概率。

　　蒙特卡罗模拟在金融工程学，宏观经济学，生物医学，计算物理学（如粒子输运计算、量子热力学计算、空气动力学计算）等领域也应用广泛。

　　计算机技术的发展，使得蒙特卡罗模拟在最近10年得到快速的普及。现代的蒙特卡罗模拟，已经不必亲自动手做实验，而是借助计算机的高速运转能力，使得原本费时费力的实验过程，变成了快速和轻而易举的事情。它不但用于解决许多复杂的科学方面的问题，也被项目管理人员经常使用。

　　借助计算机技术，蒙特卡罗模拟实现了两大优点：

　　一是简单，省却了繁复的数学报导和演算过程，使得一般人也能够理解和掌握；

　　二是快速。简单和快速，是蒙特卡罗方法在现代项目管理中获得应用的技术基础

　　蒙特卡洛法之MATLAB实现

　　蒙特卡洛法（随机取样法）也称为计算机随机模拟方法，它源于世界著名的赌城——Monte Carlo。它是基于对大量事件的统计结果来实现一些确定性问题的计算。使用蒙特卡洛法必须使用计算机生成相关分布的随机数。

　　eg：

　　y = x^2 ，y = 12 - x与X轴在第一象限与X轴围成一个曲边三角形。设计一个随机试验，求该图形的近似值。

　　其图形如下图所示：

　　x=0:0.25:12

　　y1=x.^2;

　　y2=12-x;

　　plot（x，y1，x，y2）

　　xlabel（‘x’）;ylabel（‘y’）;

　　legend（‘y1=x^2’，‘y2=12-x’）;

　　title（‘王晨绘制’）;

　　axis（［0 15 0 15］）;

　　text（3，9，‘交点’）;

　　grid on12345678910

　　

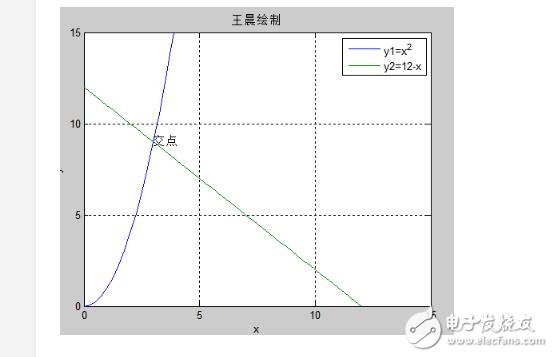
　　设计的随机试验的思想如下：在矩形区域［0，12］*［0.9］上产生服从均与分布的10^7个随机点，统计随机点落在曲边三角形内的个数，则曲边三角形的面积近似于上述矩形的面积乘以频率

　　x=unifrnd（0，12，［1，10000000］）;

　　y=unifrnd（0，9，［1，10000000］）;

　　frequency=sum（y《x.^2 & x《=3）+sum（y《12-x & x》=3）

　　area=12*9*frequency/10^71234

　　其结果如下图所示：