基于74LS192的任意进制计数器的设计

本文为大家介绍基于74LS192的任意进制计数器的设计。

74LS192的管脚图

74LS192是同步十进制可逆计数器，它由四个主从 T触发器和一些门电路组成。具有双时钟输入、清零、保持、并行置数、加计数、减计数等功能。图1为74LS192的管脚图。

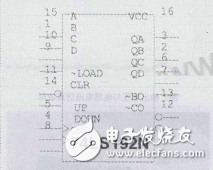
图1 74LS192的管脚图

图1中：CLR是清零端，高电平有效;UP是递加计数脉冲输入端;DOWN是递减计数脉冲输入端;～LOAD是置数控制端，低电平有效;～CO是进位输出端;～BO是借位输出端。ABCD是置数端口。

任意进制计数器M小于N的情况

假定已有的是N进制计数器，需要得到的是M进制计数器。这时就有M小于N和M大于N两种情况。

例题为用74LS192设计一个八进制计数器：

在N进制的计数器的计数顺序中，使计数器的计数状态跳过N-M的状态，就可以得到M进制计数器，如例，74LS192是一个十进制计数器，如想得到八进制计数器，输出状态QAQBQCQD需要从0000―1110状态，跳过0001及1001这两个状态。实现跳跃的方法有置零法和置数法这两个方法。

置零法的方式为在输入第M个计数脉冲CP后，利用计数器当前的输出状态SM进行译码产生清零信号加到清零端上，使计数器清零，即实现了M进制计数器。在计数器的有效循环中不包括状态SM，所以状态SM只在极短的时间内出现称为过渡状态。对于本例题来说，在输入第八个时钟脉冲后，当前的输出状态QAQBQCQD为0001，通过计数器输出端QD的高电平信号给CLR清零端，将计数器置零，回到0000状态。根据以上原理设计出的逻辑图如图2所示。

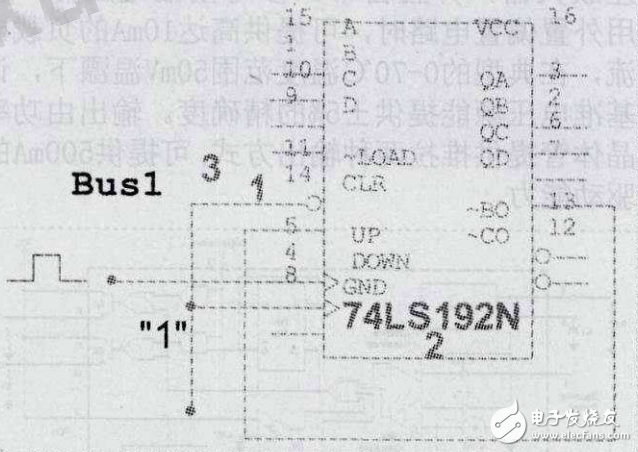
图2

置数法方式为通过给计数器置入某个数值的方法跳跃N-M的状态，从而获得M进制计数器，这种方法适用于有预置数功能的集成计数器。对于本例题来说，QAQBQCQD=0001状态与非门译码产生～LOAD=0的低电平信号，下一个时钟脉冲信号到来时将置数端ABCD=0000状态置入，跳过0001及1001这两个状态因而就实现了八进制。设计出的逻辑图如图3所示。

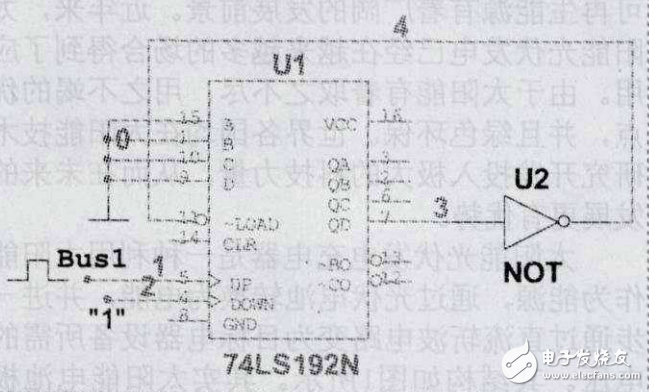
图3

任意进制计数器M大于N的情况

例题为用74LS192设计一个24进制的计数器。

设计任意进制计数器M大于N的情况时必须要使用两个以上的N进制集成电路进行组合来完成M进制计数器的设计，各个集成电路之间的连接方式可分为串行进位，并行进位，整体置零，整体置数等几种方法。

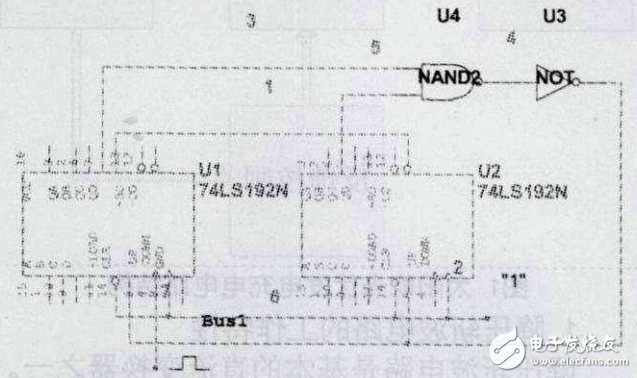
图4

整体置零法就是将两片N进制计数器级联成大于M进制的计数器，然后在计数器输出到达M状态时，通过输出状态译码出清零信号同时送达两个计数器的清零端，使两个计数器同时清零，从而实现M进制，此方法类似于M小于N的置零法原理。对于74LS192来说，就是在两片集成计数器输出端QAQBQCQD到达0010（第一片低位）0100（第二片高位）状态时，译出清零信号同时送到两个计数器的清零端。根据以上设计原理设计出下面的逻辑电路图（图4）。

整体置数法的工作原理等同于M小于N的置数法原理，首先就是将两片N进制计数器联成大于M进制的计数器，然后选定所设计的M进制状态，译码出置数端的有效工作信号，使N进制计数器置入置数输入端规定的信号，跳过剩余的不用的状态，从而实现M进制。用整体置数法使两片74LS192完成24进制的设计方法可以参考M小于N的置数法以及以上的设计例题。