如何在一个集成中使用多种模型的使用向导

人工智能和机器人研究院 2017-12-21 10440

描述

在统计学和机器学习领域，集成方法（ensemble method）使用多种学习算法以获得更好的预测性能（相比单独使用其中任何一种算法）。和统计力学中的统计集成（通常是无穷集合）不同，一个机器学习集成仅由一个离散的可选模型的离散集合组成，但通常拥有更加灵活的结构 [1]。

使用集成的主要动机是在发现新的假设，该假设不一定存在于构成模型的假设空间中。从经验的角度看，当模型具有显著的多样性时，集成方法倾向于得到更好的结果 [2]。

动机

在一个大型机器学习竞赛的比赛结果中，最好的结果通常是由模型的集成而不是由单个模型得到的。例如，ILSVRC2015 的得分最高的单个模型架构得到了第 13 名的成绩。而第 1 到 12 名都使用了不同类型的模型集成。

我目前并没有发现有任何的教程或文档教人们如何在一个集成中使用多种模型，因此我决定自己做一个这方面的使用向导。

我将使用 Keras，具体来说是它的功能性 API，以从相对知名的论文中重建三种小型 CNN（相较于 ResNet50、Inception 等而言）。我将在 CIFAR-10 数据集上独立地训练每个模型 [3]。然后使用测试集评估每个模型。之后，我会将所有三个模型组成一个集合，并进行评估。通常按照预期，这个集成相比单独使用其中任何一个模型，在测试集上能获得更好的性能。

有很多种不同类型的集成：其中一种是堆叠（stacking）。这种类型更加通用并且在理论上可以表征任何其它的集成技术。堆叠涉及训练一个学习算法结合多种其它学习算法的预测 [1]。对于这个示例，我将使用堆叠的最简单的一种形式，其中涉及对集成的模型输出取平均值。由于取平均过程不包含任何参数，这种集成不需要训练（只需要训练模型）。

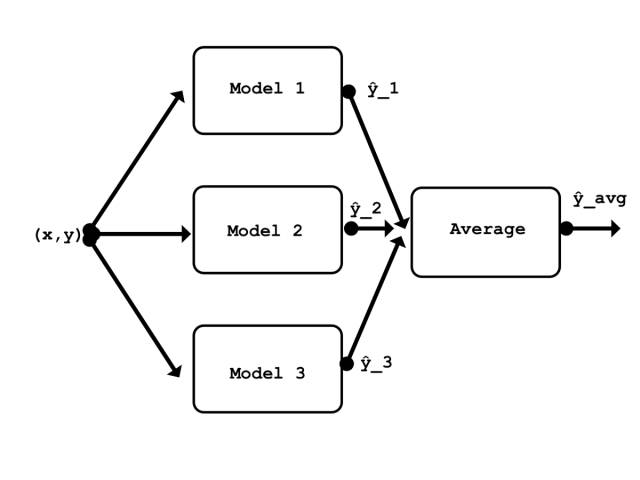
本文介绍的集成的简要结构

准备数据

首先，导入类和函数：

fromkeras.modelsimportModel,Input
fromkeras.layersimportConv2D,MaxPooling2D,GlobalAveragePooling2D,Activation,Average,Dropout
fromkeras.utilsimportto_categorical
fromkeras.lossesimportcategorical_crossentropy
fromkeras.callbacksimportModelCheckpoint,TensorBoard
fromkeras.optimizersimportAdam
fromkeras.datasetsimportcifar10
importnumpyasnp

我使用的数据集是 CIFAR-10，因为很容易找到在这个数据集上工作得很好的架构的相关论文。使用一个流行的数据集还可以令这个案例容易复现。

以下是数据集的导入代码。训练数据和测试数据都已经归一化。训练标签向量被转换成一个 one-hot 矩阵。不需要转换测试标签向量，因为它不会在训练中使用。

(x_train, y_train), (x_test, y_test) = cifar10.load_data()
x_train = x_train /255.
x_test = x_test /255.
y_train = to_categorical(y_train, num_classes=10)

数据集由 6 万张 10 个类别的 32x32 的 RGB 图像组成。其中 5 万张用于训练/验证，其它 1 万张用于测试。

print('x_train shape: {} |
y_train shape: {}\nx_test shape : {} |
y_test shape : {}'.format(x_train.shape, y_train.shape, x_test.shape, y_test.shape))

>>> x_train shape: (50000, 32, 32, 3) | y_train shape: (50000, 10)

>>> x_test shape : (10000, 32, 32, 3) | y_test shape : (10000, 1)

由于三个模型使用的是相同类型的数据，定义单个用于所有模型的输入层是合理的。

input_shape = x_train[0,:,:,:].shape
model_input =Input(shape=input_shape)

第一个模型：ConvPool-CNN-C

第一个将要训练的模型是 ConvPool-CNN-C[4]。它使用了常见的模式，即每个卷积层连接一个池化层。唯一一个对一些人来说可能不熟悉的细节是其最后的层。它使用的并不是多个全连接层，而是一个全局平均池化层（global average pooling layer）。

以下是关于全局池化层的工作方式的简介。最后的卷积层 Conv2D(10，(1，1)) 输出和 10 个输出类别相关的 10 个特征图。然后 GlobalAveragePooling2D() 层计算这 10 个特征图的空间平均（spatial average），意味着其输出是一个维度为 10 的向量。之后，对这个向量应用一个 softmax 激活函数。如你所见，这个方法在某种程度上类似于在模型的顶部使用全连接层。可以在这篇论文 [5] 中查看更多关于全局池化层的内容。

重要事项：不要对最后的 Conv2D(10，(1，1)) 层的输出直接应用激活函数，因为这个层的输出需要先输入 GlobalAveragePooling2D()。

defconv_pool_cnn(model_input):
x =Conv2D(96, kernel_size=(3,3), activation='relu', padding = 'same')(model_input)
x =Conv2D(96, (3,3), activation='relu', padding ='same')(x)
x =Conv2D(96, (3,3), activation='relu', padding ='same')(x)
x =MaxPooling2D(pool_size=(3,3), strides =2)(x)
x =Conv2D(192, (3,3), activation='relu', padding ='same')(x)
x =Conv2D(192, (3,3), activation='relu', padding ='same')(x)
x =Conv2D(192, (3,3), activation='relu', padding ='same')(x)
x =MaxPooling2D(pool_size=(3,3), strides =2)(x)
x =Conv2D(192, (3,3), activation='relu', padding ='same')(x)
x =Conv2D(192, (1,1), activation='relu')(x)
x =Conv2D(10, (1,1))(x)
x =GlobalAveragePooling2D()(x)
x =Activation(activation='softmax')(x)
model =Model(model_input, x, name='conv_pool_cnn')
returnmodel

用具体例子解释该模型

conv_pool_cnn_model = conv_pool_cnn(model_input)

为了简单起见，每个模型都使用相同的参数进行编译和训练。其中，epoch 数等于 20、批尺寸等于 32（每个 epoch 进行 1250 次迭代）的参数设置能使三个模型都找到局部极小值。随机选择训练集的 20% 作为验证集。

defcompile_and_train(model, num_epochs):
model.compile(loss=categorical_crossentropy, optimizer=Adam(), metrics=['acc'])
filepath ='weights/'+ model.name +'.{epoch:02d}-{loss:.2f}.hdf5'
checkpoint =ModelCheckpoint(filepath, monitor='loss', verbose=0, save_weights_only=True, save_best_only=True, mode='auto', period=1)
tensor_board =TensorBoard(log_dir='logs/', histogram_freq=0, batch_size=32)
history = model.fit(x=x_train, y=y_train, batch_size=32, epochs=num_epochs, verbose=1, callbacks=[checkpoint, tensor_board], validation_split=0.2)
returnhistory

大约需要每 epoch1 分钟的时间训练这个（以及下一个）模型，我们使用了单个 Tesla K80 GPU。如果你使用的是 CPU，可能需要花较多的时间。

_ = compile_and_train(conv_pool_cnn_model, num_epochs=20)

该模型达到了大约 79% 的验证准确率。

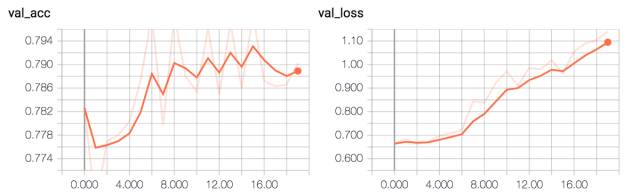
ConvPool-CNN-C 验证准确率和损失

通过计算测试集的误差率对模型进行评估。

defevaluate_error(model):
pred=model.predict(x_test,batch_size=32)
pred=np.argmax(pred,axis=1)
pred=np.expand_dims(pred,axis=1)# make same shape as y_test
error=np.sum(np.not_equal(pred,y_test))/y_test.shape[0]
returnerror
evaluate_error(conv_pool_cnn_model)

>>> 0.2414

第二个模型：ALL-CNN-C

下一个模型，ALL-CNN-C，来自同一篇论文 [4]。这个模型和上一个很类似。唯一的区别是用步幅为 2 的卷积层取代了最大池化层。再次，需要注意，在 Conv2D(10，(1，1)) 层之后不要立刻应用激活函数，如果在该层之后应用了 ReLU 激活函数，会导致训练失败。

defall_cnn(model_input):
x=Conv2D(96,kernel_size=(3,3),activation='relu',padding='same')(model_input)
x=Conv2D(96,(3,3),activation='relu',padding='same')(x)
x=Conv2D(96,(3,3),activation='relu',padding='same',strides=2)(x)
x=Conv2D(192,(3,3),activation='relu',padding='same')(x)
x=Conv2D(192,(3,3),activation='relu',padding='same')(x)
x=Conv2D(192,(3,3),activation='relu',padding='same',strides=2)(x)
x=Conv2D(192,(3,3),activation='relu',padding='same')(x)
x=Conv2D(192,(1,1),activation='relu')(x)
x=Conv2D(10,(1,1))(x)
x=GlobalAveragePooling2D()(x)
x=Activation(activation='softmax')(x)
model=Model(model_input,x,name='all_cnn')
returnmodel
all_cnn_model=all_cnn(model_input)
_=compile_and_train(all_cnn_model,num_epochs=20)

该模型收敛到了大约 75% 的验证准确率。

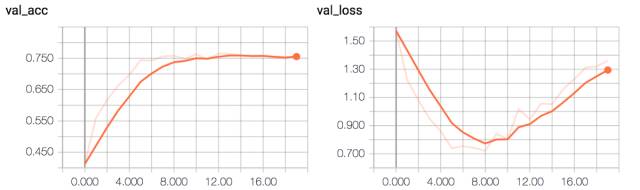
ConvPool-CNN-C 验证准确率和损失

由于这两个模型很相似，误差率差别不大。

evaluate_error(all_cnn_model)

>>> 0.26090000000000002

第三个模型：Network In Network CNN

第三个 CNN 是 Network In Network CNN[5]。这个模型来自引入了全局池化层的论文。它比之前的两个模型更小，因此其训练速度更快。（再提醒一次，不要在最后的卷积层之后使用 ReLU 函数！）

相较于在 MLP 卷积层中使用多层感知机，我使用的是 1x1 卷积核的卷积层。从而需要优化的参数变得更少，训练速度进一步加快，并且还获得了更好的结果（当使用全连接层的时候无法获得高于 50% 的验证准确率）。该论文中称，MLP 卷积层中应用的函数等价于在普通卷积层上的级联跨通道参数化池化（cascaded cross channel parametric pooling），其中依次等价于一个 1x1 卷积核的卷积层。如果这个结论有错误，欢迎指正。

defnin_cnn(model_input):
#mlpconv block 1
x=Conv2D(32,(5,5),activation='relu',padding='valid')(model_input)
x=Conv2D(32,(1,1),activation='relu')(x)
x=Conv2D(32,(1,1),activation='relu')(x)
x=MaxPooling2D((2,2))(x)
x=Dropout(0.5)(x)
#mlpconv block2
x=Conv2D(64,(3,3),activation='relu',padding='valid')(x)
x=Conv2D(64,(1,1),activation='relu')(x)
x=Conv2D(64,(1,1),activation='relu')(x)
x=MaxPooling2D((2,2))(x)
x=Dropout(0.5)(x)
#mlpconv block3
x=Conv2D(128,(3,3),activation='relu',padding='valid')(x)
x=Conv2D(32,(1,1),activation='relu')(x)
x=Conv2D(10,(1,1))(x)
x=GlobalAveragePooling2D()(x)
x=Activation(activation='softmax')(x)
model=Model(model_input,x,name='nin_cnn')
returnmodel
nin_cnn_model=nin_cnn(model_input)

这个模型的训练速度快得多，在我的机器上每个 epoch 只要 15 秒就能完成。

_=compile_and_train(nin_cnn_model,num_epochs=20)

该模型达到了大约 65% 的验证准确率。

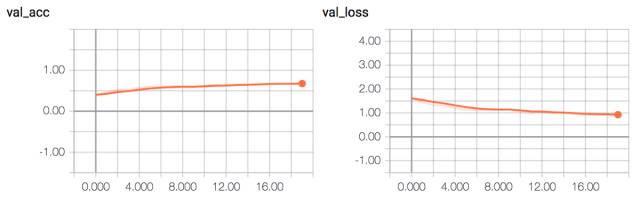
NIN-CNN 验证准确率和损失

这个模型比之前的两个模型简单得多，因此其误差率要高一点。

evaluate_error(nin_cnn_model)

>>> 0. 0.31640000000000001

三个模型的集成

现在将这三个模型组合成一个集成。

所有三个模型都被重新实例化并加载了最佳的已保存权重。

conv_pool_cnn_model=conv_pool_cnn(model_input)
all_cnn_model=all_cnn(model_input)
nin_cnn_model=nin_cnn(model_input)
conv_pool_cnn_model.load_weights('weights/conv_pool_cnn.29-0.10.hdf5')
all_cnn_model.load_weights('weights/all_cnn.30-0.08.hdf5')
nin_cnn_model.load_weights('weights/nin_cnn.30-0.93.hdf5')
models=[conv_pool_cnn_model,all_cnn_model,nin_cnn_model]

集成模型的定义是很直接的。它使用了所有模型共享的输入层。在顶部的层中，该集成通过使用 Average() 合并层计算三个模型输出的平均值。

defensemble(models,model_input):
outputs=[model.outputs[0]formodelinmodels]
y=Average()(outputs)
model=Model(model_input,y,name='ensemble')
returnmodel
ensemble_model=ensemble(models,model_input)

不出所料，相比于任何单一模型，集成有着更低的误差率。

evaluate_error(ensemble_model)

>>> 0.2049

其他可能的集成

为了完整性，我们可以查看由两个模型组合组成的集成的性能。相比于单一模型，前者有更低的误差率。

pair_A=[conv_pool_cnn_model,all_cnn_model]
pair_B=[conv_pool_cnn_model,nin_cnn_model]
pair_C=[all_cnn_model,nin_cnn_model]
pair_A_ensemble_model=ensemble(pair_A,model_input)
evaluate_error(pair_A_ensemble_model)

>>> 0.21199999999999999

pair_B_ensemble_model=ensemble(pair_B,model_input)
evaluate_error(pair_B_ensemble_model)

>>> 0.22819999999999999

pair_C_ensemble_model=ensemble(pair_C,model_input)
evaluate_error(pair_C_ensemble_model)

>>>0.2447

结论

重申一下介绍中的内容：每个模型有其自身的缺陷。使用集成背后的原因是通过堆叠表征了关于数据的不同假设的不同模型，我们可以找到一个更好的假设，它不在一个从其构建集成的模型的假设空间之中。

与在大多数情况下使用单个模型相比，使用一个非常基础的集成实现了更低的误差率。这证明了集成的有效性。

当然，在使用集成处理你的机器学习任务时，需要牢记一些实际的考虑。由于集成意味着同时堆栈多个模型，这也意味着输入数据需要前向传播到每个模型。这增加了需要被执行的计算量，以及最终的评估（预测）时间。如果你在研究或 Kaggle 竞赛中使用集成，增加的评估时间并不重要，但是在设计一个商业化产品时却非常关键。另一个考虑是最后的模型增加的大小，它会再次成为商业化产品中集成使用的限制性因素。

参考文献

1. Ensemble Learning. (n.d.). In Wikipedia. Retrieved December 12, 2017, from https://en.wikipedia.org/wiki/Ensemble_learning

2. D. Opitz and R. Maclin (1999)「Popular Ensemble Methods: An Empirical Study」, Volume 11, pages 169–198 (http://jair.org/papers/paper614.html)

3. Learning Multiple Layers of Features from Tiny Images, Alex Krizhevsky, 2009.

4. Striving for Simplicity: The All Convolutional Net：arXiv:1412.6806v3 [cs.LG]

5. Network In Network：arXiv:1312.4400v3 [cs.NE]

打开APP阅读更多精彩内容