石墨烯掺杂载流子诱导RKKY的物理机制 实现对原子间自旋交换作用及其调制

纳米尺度的磁性小团簇（由数个原子组成）是构建纳米磁性器件和自旋电子器件的基本单元，也是研究磁性原子间自旋交换相互作用的理想体系。如何在原子尺度上直接测量和研究两个磁性原子间的自旋耦合强度，实现对其自旋交换作用的调控是十分重要的基础问题，在实验上面临的困难和挑战主要是如何构建具有相互作用的由两个或有限数量磁性原子构成的团簇。制备磁性原子团簇的方法通常只能在几种有限的基底表面（通常为金属或者绝缘衬底）利用外延技术或刻蚀手段实现，但是其结构难以在原子尺度实现精确控制。磁性原子团簇在弱相互作用基底上的可控生长一直是研究磁性原子间自旋交换作用的重要前沿课题。

石墨烯是一类重要的自旋电子材料，在未来自旋电子器件中具有潜在的应用价值。近年来, 中国科学院物理研究所/北京凝聚态物理国家实验室（筹）高鸿钧研究组在高质量石墨烯的可控生长及物性研究方面取得了一系列突破性进展。他们提出了基于单晶表面外延的高质量、大面积的石墨烯生长技术，在国际上率先实现了在Ru(0001)表面获得缺陷可控、1个厘米大小的、连续的单晶石墨烯[Chin. Phys. 16, 3151(2007); Adv. Mater. 21, 2777 (2009)]，并对其物理性质和结构调制进行了系列研究[J. Am. Chem. Soc. 131, 14136(2009); Phys. Rev. Lett. 105, 219701 (2010); J. Phys.: Condens. Matter 22, 302001 (2010) (Cover Story),Appl. Phys. Lett. 100, 093101 (2012)(Cover story); 100, 083101 (2012) ; 102, 093106 (2013)]。Ru(0001)表面上外延生长的石墨烯不仅具有大面积、高质量的特性，还拥有天然的周期性摩尔（Moiré）超晶格结构，利用金属基底对石墨烯的电子掺杂，高鸿钧研究组在实验上首次观测到了单个磁性钴原子的近藤效应，并利用摩尔超晶格实现了对近藤效应的可控调制[Nano Letters, 14, 4011 (2014)]。      近期，他们利用这一石墨烯摩尔超晶格结构为模板，开展了磁性原子间的自旋耦合相互作用的研究。该研究组的博士生任金东、武旭和郭海明研究员等利用极低温矢量磁场扫描隧道显微镜/扫描隧道谱（STM/STS）技术，以Ru(0001)单晶上的单层石墨烯为基底，采用原位低温沉积技术，实现了锰原子团簇（二聚体和三聚体）的可控制备和选择性吸附，在实验上首次探测到不同锰原子团簇内部的原子间自旋交换作用并实现了可控调制。两个锰原子形成的二聚体团簇的扫描隧道谱展现出一个从单重态基态到三重态基态的激发台阶，施加磁场后激发台阶发生三级劈裂，两个原子之间为反铁磁耦合，耦合强度受其在石墨烯基底的吸附位置和原子间距离调制。对于更为复杂的锰三聚体团簇结构，STS谱线上观察到多级自旋激发，并呈现不同的磁场响应特性，结合海森堡自旋模型，证明团簇内原子非共线排列，同时获得原子间自旋耦合类型以及强度等信息。当形成具有三角形结构的锰三聚体时，其中两个锰原子形成类似上述二聚体的反铁磁耦合，第三个锰原子和另两个锰原子均形成铁磁耦合。该研究组的博士生潘金波、张艳芳和杜世萱研究员，物理所杨义峰研究员与美国马里兰大学欧阳敏教授等合作进行了第一性原理及海森堡自旋模型理论计算，结果表明，石墨烯/Ru的摩尔周期不同区域的电子结构差异是影响和调制锰磁性原子间反铁磁耦合强度的主要原因。进一步分析发现，锰原子之间除了直接的自旋交换作用外，还存在着非局域的Ruderman-Kittel-Kasuya-Yosida (RKKY)间接交换作用，与石墨烯基底的掺杂载流子浓度有关。

该项工作首次在实验上直接在原子尺度实现了对磁性原子间自旋相互作用的调制，验证了石墨烯掺杂载流子诱导 RKKY 的物理机制，提供了一条在原子尺度上调控磁性原子间自旋耦合，以及不同自旋类型团簇可控自组装的潜在途径。相关研究结果发表在 Phys. Rev. Lett. 119, 176806 (2017)上。

此项工作得到了科技部973（No. 2013CBA01600, 2013CB932901, 2016YFA0202300）、国家自然科学基金委（No. 11574363, 61274011, 61390501, 51325204）和中国科学院等计划的支持。

图一：a) 石墨烯/Ru(0001)摩尔周期结构上吸附的锰原子团簇示意图；b) 石墨烯摩尔周期不同位置上吸附锰原子二聚体的数目比例统计；c) 不同吸附位置锰二聚体的STM图和对应的STS谱线。

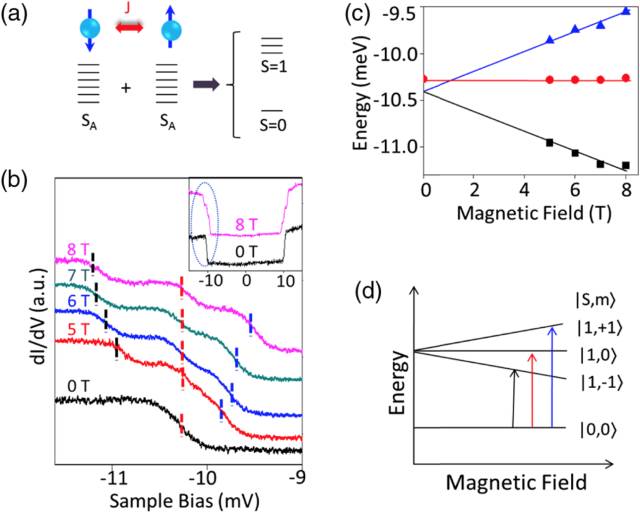
图二：a) 锰二聚体内反铁磁耦合示意图；b) 锰二聚体的自旋激发谱，显示零场（0 T）下的自旋激发台阶在磁场（5, 6, 7 和8 T）下发生三重劈裂。c) 劈裂能（由图b中拟合）随着磁场强度的增大而增加。d) 磁场下锰二聚体从单态到三重态跃迁的示意图。

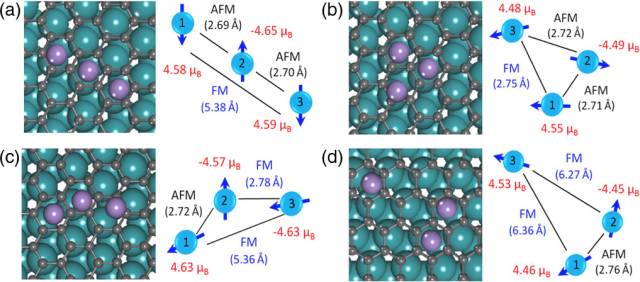
图三：DFT计算得到的石墨烯/Ru上吸附锰三聚体的四种稳定优化构型。根据其原子间自旋耦合类型的不同，可分为AFM-AFM-FM (a and b) 和AFM-FM-FM (c and d)两大类。

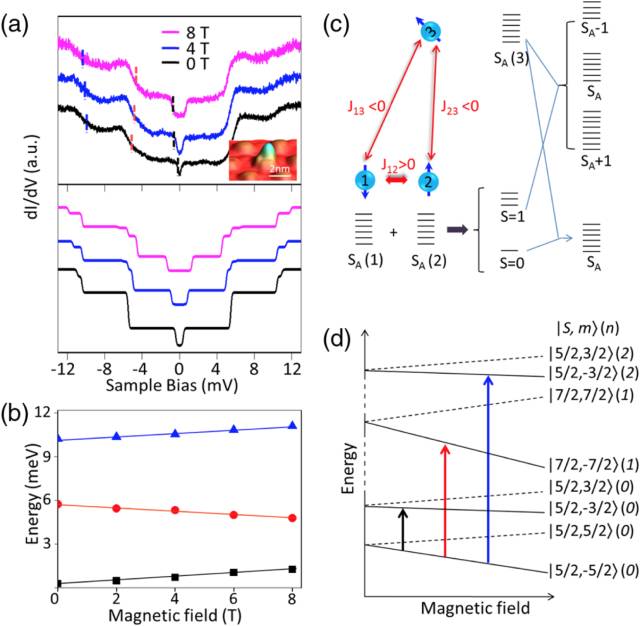
图四：a) 锰三聚体实验得到的自旋激发谱线（上）和理论模拟谱线（下）(AFM-FM-FM模型，其中J12 = 8.9 meV, J13= J23 = -1.3 meV, D= -0.08 meV )的对比。b) 由图a实验谱线得到的激发台阶偏移能量随磁场强度的变化关系。c) 锰三聚体（AFM-FM-FM模型）能级及其简并度的示意图。d) 磁场下锰三聚体从基态到激发态跃迁的示意图。