小波阈值去噪的基本原理_小波去噪阈值如何选取

小波阈值去噪的基本原理

小波阈值去噪的基本思想是先设置一个临界阈值λ，若小波系数小于λ，认为该系数主要由噪声引起，去除这部分系数;若小波系数大于λ，则认为此系数主要是由信号引起，保留这部分系数，然后对处理后的小波系数进行小波逆变换得到去噪后的信号。具体步骤如下：

（1）对带噪信号f（t）进行小波变换，得到一组小波分解系数Wj，k;

（2）通过对小波分解系数Wj，k进行阈值处理，得到估计小波系数Wj，k，使Wj，k－uj，k尽可能的小;

（3）利用估计的小波系数Wj，k进行小波重构，得到估计信号f（t），即为去噪后的信号。

提出了一种非常简洁的方法对小波系数Wkj，进行估计。对f（k）连续做几次小波分解后，有空间分布不均匀信号s（k）各尺度上小波系数Wkj，在某些特定位置有较大的值，这些点对应于原始信号s（k）的奇变位置和重要信息，而其他大部分位置的Wkj，较小；对于白噪声n（k），它对应的小波系数Wkj，在每个尺度上的分布都是均匀的，并随尺度的增加Wkj，系数的幅值减小。因此，通常的去噪办法是寻找一个合适的数作为阈值（门限），把低于λ的小波函数Wkj，（主要由信号n（k）引起），设为零，而对于高于的小波函数Wkj，（主要由信号s（k）引起），则予以保留或进行收缩，从而得到估计小波系数Wkj，它可理解为基本由信号s（k）引起，然后对Wkj进行重构，就可以重构原始信号。

本文提出的小波阈值去噪方法可以分为5步描述：

（1）对带噪图像g（i，j）进行s层正交冗余小波变换，得到一组小波分解系数Wg（i，j）（s，j），其中j=1，2，…s，s表示小波分解的层数。

小波去噪阈值如何选取

小波阈值去噪法有着很好的数学理论支持，实现简单而又非常有效，因此取得了非常大的成功，并吸引了众多学者对其作进一步的研究与改进。这些研究集中在两个方面：对阈值选取的研究以及对阈值函数的研究。

阈值的确定在去噪过程中至关重要，目前使用的阈值可以分为全局阈值和局部适应阈值两类。其中，全局阈值是对各层所有的小波系数或同一层内不同方向的小波系数都选用同一个阈值。而局部阈值是根据不同层不同方向分别选取阈值。

（1）全局阈值。

全局阈值按下式计算

其中：

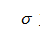为噪声标准差，M，N为图像信号的尺度。

该阈值是在高斯模型下针对多维独立正态变量联合分布得出的;

（2）基于零均值正态分布的置信区间阈值。

置信区间阈值的计算式为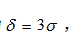此阈值是考虑零均值的正态分布变量落在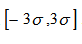之外的概率非常小，所以，绝对值大于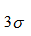的系数一般都认为主要由信号系数构成。

（3）最小最大化阈值。

这是在最小最大化意义下得出的阈值，它没有显示表达式，而且要预先知道原信号才能求取阈值。

（4）TOP阈值。

TOP阈值的计算式为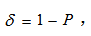其中P是需要保留的大的小波系数的比率。这种阈值选取方法没有理论上的最优准则，但可以允许选择不同的P来多次实验恢复图像。

（5）SUREShrink阈值。

基于SURE（Stein’SUnbiasedRiskEstimation）准则的SUREShrink阈值：

（7）自适应阈值。

利用自适应方法确定小波系数的阈值。阈值的确定在阈值萎缩中是最关键的，虽然用Donoho的软阈值去噪法能取得不错的效果，但因白噪声具有负的奇异性，其幅值和稠密度随尺度增加而减少，而信号则是相反。因此随着尺度级数的增加，由噪声所控制的模极大值的幅度和稠密度会明显增大。所以在每级尺度上都采用同一阈值显然不合适；在较低尺度上，会去除有用信号；而到了最大尺度级，则会留下一部分噪声。因此可以考虑选择自适应阈值克服这种缺点。自适应阈值就是将每级尺度都视为相互独立，根据每级尺度上小波系数幅值的不同特点，分别在每层分解3个方向，分别是水平方向、竖直方向和对角方向，并且在每个方向上寻找一个与之最匹配的阈值来进行除噪，这样就可以把所有方向的噪声分离出来。利用自适。

在以上阈值中，全局阈值计算简单，但是它趋向于“过扼杀”小波系数，在重构时会导致较大误差：置信区间阈值虽然与图像尺寸无关。但由于随着图像尺寸的增大，大的噪声系数出现的数目会增多，并被保留，因而导致误差增大；最小最大化阈值，由于基于悲观决策的思想，所以也会“过扼杀”系数；SURE阈值效果最优但求解阈值过程复杂；BayesShrink的效果仅次于SURE，但算法简单。