

基于新阈值函数的小波阈值去噪算法
嵌入式设计应用
描述
小波变换以其多分辨率分析的特性,在时频域内良好的表征信号的能力以及大小固定形状可变的窗口等特点,广泛应用于图像去噪中,并得到了很好的去噪效果。而小波阈值去噪法是小波分析法在图像去噪众多应用中最常用的一种方法,利用阈值处理后的小波系数进行小波反变换重构出去噪后的结果图像。在小波阈值去噪法中的两个重要的因素—阈值选取方式和阈值函数,直接决定图像去噪的效果,所以要针对噪声和图像选取合适的阈值函数和最佳阈值,才能最大程度去除图像噪声。
本文提出了新的阈值函数,这一函数既满足函数的连续性,又解决了阈值函数恒定偏差问题。
1、小波阈值去噪原理
小波阈值去噪方法中噪声通常处于高频,利用这一特点,通过对高频部分进行相应阈值化处理,然后进行重构,这样就达到了去除噪声的目的。
假设一幅图像被高斯噪声污染的表示形式如下:

为含噪声图像;nj,k为高斯白噪声,服从正态分布N(0,δ^2)正态分布。
小波阈值方法通过以下3步骤进行实现:
1)对fj,k作小波变换,得到小波系数wj,k;
2)通过对wj,k进行阈值化处理,得出小波估计系数w^j,k;
3)利用w^j,k进行小波系数重新构造得到去噪后的图像f^j,k。
常用的阈值求法有:斯坦无偏似然估计准则、固定阈值准则、启发式阈值准则和极大极小原理准则。本文采用固定阈值准则固定阈值定义如下:

其中:M×N为图像的大小。
2、小波阈值函数
2.1、常见的小波阈值函数
小波阈值去噪法的另一种称呼是阈值函数,也就是利用阈值函数来获得阈值,阈值函数应用最多的就是Donoho等提出的阈值的方法,而且Donoho等也证明了利用小波阈值去噪比其他经典的去噪方法优越。随后人们在此基础上提出了改进的阈值函数,如硬软折中阈值函数等。硬、软阈值函数分别如式(3)(4)。
硬阈值函数定义为:
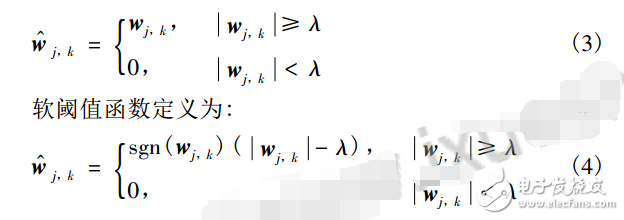
2.2、改进的小波阈值函数
硬、软阈值方法在去噪方面取得了较好的效果,但它们存在缺点。式(3)虽然解决了|w^j,k-wj,k|的误差问题,但存在间断点±λ,在图像重建时会产生一些附加震荡,而且比较容易出现Pseudo-Gibbs现象等视觉失真。同样,式(4)在±λ处连续性好,但|w^j,k-wj,k|存在恒定的误差,这样会使图像的高频信息产生丢失等失真的现象,且式(4)存在高阶求导的困难,不利于进一步用数学工具对它处理。硬软折中阈值函数对式(3)(4)进行了改进,但依然存在恒定偏差问题。
为了更好地解决以上方法所带来的问题,文献分别提出了如下的改进的阈值函数:
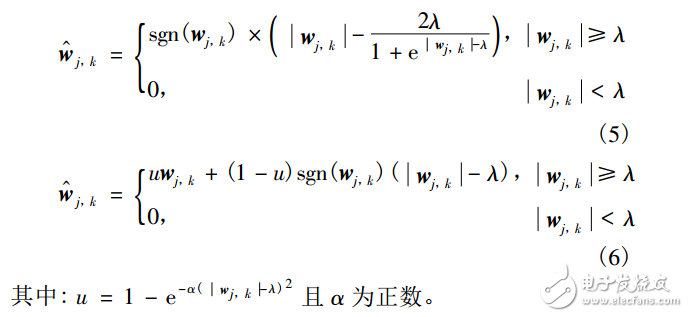
式(5)很好地解决了含噪图像的小波系数与估计小波系数恒等的误差问题,但它没有调节因子,显然不够灵活,而且连续性差;式(6)虽然解决了连续性问题,但含噪图像的小波系数与估计小波系数的恒定偏差还是没有得到很好的解决。为了能够有效解决上述问题,本文提出了新的函数:
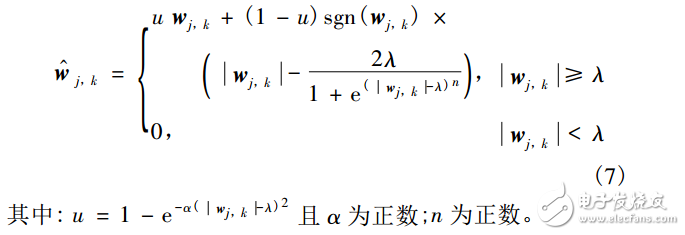
图1的横坐标为对fj,k经过小波变换得到的原始的小波系数;纵坐标为对小波系数进行阈值处理后的得到的估计的小波系数。λ为门限值;根据式(7)的函数进行绘图。图1中,λ=5,原始小波系数取值范围为-20~20。
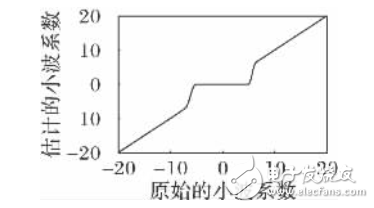
图1 α=1,n=3时改进阈值函数
2.2.1、改进的阈值函数分析
从数学的角度对式(7)进行如下分析。
1)函数的连续性。

综上所述:新阈值函数在±λ处连续。
2)函数的渐近性
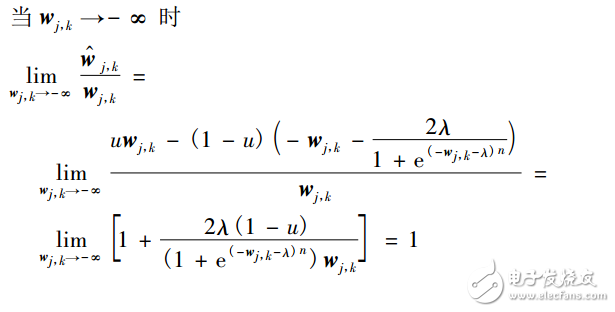

综上所述:函数式(7)是以w^j,k=wj,k为渐近线的,也就是说,新阈值函数以w^j,k=wj,k为渐近线。
3)阈值函数的偏差性。
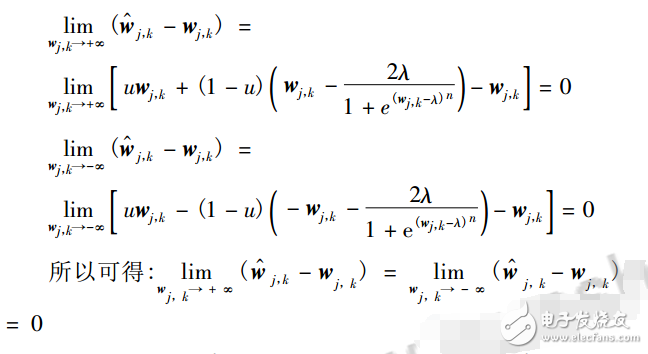
随着wj,k→∞,w^j,k逐渐接近wj,k,从而克服了w^j,k与wj,k之间具有偏差的问题。
4)函数的高阶可导性。
当|wj,k|≥λ时,新阈值函数满足高阶可导,所以便于进行各种数学处理。
5)阈值可变因子α与n影响分析。
当α=0,n=1时,新阈值函数为式(5);当α=0,n→0时,新阈值函数为软阈值函数,当n→∞时新阈值函数为硬阈值函数;
当α→∞时新阈值函数就变成为硬阈值函数;因此与式(5)和式(6)相比,新阈值函数不仅具有整体连续性的优点,而且根据实际应用调节非常灵活。
2.2.2、改进的阈值函数去噪算法步骤
第1步选择合适的小波基函数,小波基一般根据具体噪声图像的特点进行选择。然后对带噪声图像式(1)中fj,k进行多层次正交小波变换,得到一组小波分解系数wj,k,其中:wj,1∈{LHj}(j层水平方向小波系数);wj,2∈{HLj}(j层垂直方向小波系数);wj,3∈{HHj}(j层对角线方向小波系数);(j=1,2,…,l,l表示小波分解的层数)。
第2步对式(1)中噪声nj,k方差δ进行估计,噪声方差δ=median(w1,3/c),其中c是常数,一般取0.6745。然后在求出δ的基础上,根据式(2)求出门限阈值λ的值。
第3步以λ为门限,分别根据式(7)对LHj,HLj,HHj系数进行阈值处理,得到估计的小波系数w^j,k。
第4步根据所得w^j,k小波系数以及其他没有进行阈值处理的低频部分的小波系数利用小波基函数进行小波重新构造,从而得到去噪后的图像f^j,k即f^j,k就是所要求的图像。
3、实验结果及分析
为了证明改进阈值函数去噪的有效性,使用Matlab软件对加0.01的高斯白噪的Lena和Cameraman图像分别用经典的软、硬阈值函数、硬软折中阈值函数以及改进的阈值函数进行仿真实验。本文基于提升图像的对称性,视觉好,更适合于图像处理,因而选择coif4基函数,进行四层分解与重构,并进行阈值去噪。去噪效果如图2所示。
图2 对Lena图像不同方法降噪结果
图3 对Cameraman图像不同方法降噪结果
为了进一步衡量本文提出新阈值函数的性能,用均方差(MeanSquaredError,MSE)与峰值信噪比(PeakSignal-toNoiseRatio,PSNR)对去噪后效果析。MSE的值越小表示图像的质量越好;PSNR的值越大图像的质量越好。它们分别定义为:
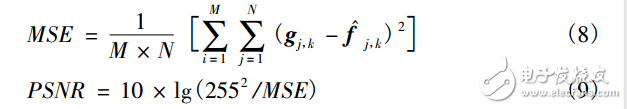
其中:M×N为图像大小,gj,k是无噪图像,f^j,k为去噪得到的图像。
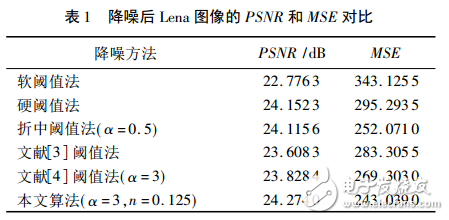
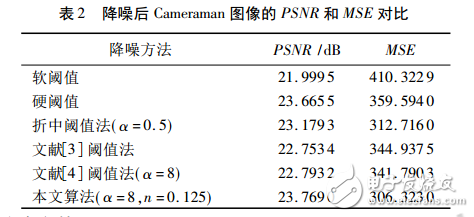
通过仿真实验表明:基于改进阈值函数的小波去噪比基于软阈值函数、硬阈值函数、硬软折中阈值函数、文献阈值函数、阈值函数得到较大的峰值信噪比和较小的均方误差。实验具体的结果如表1、表2所示。由图2、图3可以看出改进阈值函数的小波去噪效果较好。
4、结语
本文在分析了Dohono软硬阈值、硬软折中阈值函数的优缺点后,提出了对阈值函数的改进算法。这一阈值函数含有两个调节阈值因子α和n,通过改变这两个参数,达到最佳小波系数阈值的估计,经过实验证明,改进的阈值函数能够较好地去除图像噪声,且可以保护图像的细节信息。
-
 llsluoluo33
2018-08-12
0 回复 举报我是主动降噪芯片中国原厂的,可提供降噪方案和降噪芯片,协助解决技术难点,电话和微信18503002452 qq 2208962322 收起回复
llsluoluo33
2018-08-12
0 回复 举报我是主动降噪芯片中国原厂的,可提供降噪方案和降噪芯片,协助解决技术难点,电话和微信18503002452 qq 2208962322 收起回复
-
小波阈值去噪的基本原理是什么?2020-11-06 3079
-
小波去噪阈值如何选取_小波阈值分析2018-01-10 61987
-
基于EEMD和模糊阈值的去噪方法2017-11-21 1231
-
新阈值函数的自适应去噪2017-01-03 727
-
GIS局部放电小波阈值去噪算法的改进2015-12-18 953
-
小波阈值去噪改进算法研究2011-06-22 1150
-
基于一种新阈值函数的小波医学图像去噪2010-01-15 848
-
一种自适应多尺度积阈值的图像去噪算法2009-11-11 598
全部0条评论

快来发表一下你的评论吧 !

