基于神经网络的激活函数和相应的数学介绍

最近我有一个同事老是问我“为什么我们用这么多激活函数？”，“为什么这个函数效果比那个好？”，“你怎么知道要用哪个函数？”，“这是很难的数学？”等等。所以我想，我何不给对神经网络只有基本了解的人写篇文章，介绍下激活函数和相应的数学呢？

注意：本文假设你对人工“神经元”有基本的了解。

激活函数

简单来说，人工神经元计算输入的“加权和”，加上偏置，接着决定是否需要“激活”（好吧，其实是激活函数决定是否激活，但是现在让我们先这样理解吧）。

考虑一个神经元。

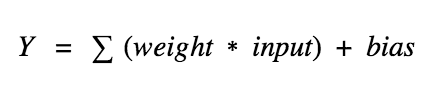
上式中，Y的值可能是负无穷大到正无穷大之间的任意值。神经元并不知道值的界限。所以我们如何决定神经元是否需要激活呢？

为此，我们决定增加“激活函数”。

阶跃函数

我们首先想到的是一个基于阈值的激活函数。如果Y的值大于一个特定值，就定义为“激活”。如果小于阈值，则不激活。

激活函数 A = “激活” if Y > 阈值 else not

或者，A = 1 if Y > 阈值, 否则 0

好吧，我们刚刚定义的是一个阶跃函数（step function）。

当值大于0（阈值）时，输出为1（激活），否则输出为0（不激活）。

很好。很清楚，这可以作为神经元的激活函数。然而，这个方法有一些特定的缺陷。

假设你正创建一个二元分类器，输出“是”或“否”（激活或未激活）。一个阶跃函数可以做到这一点。实际上这正是阶跃函数做的事，输出1或0。然后，想想如果你想要连接更多这样的神经元来引入更多的分类，比如类一、类二、类三，等等。当不止一个神经元“激活”时会发生什么？所有的神经元将输出1（基于阶跃函数）。然后你如何决定最终结果属于哪个分类呢？嗯，很难，很复杂。

你可能想要用当且仅当一个神经元输出为1来表示分类结果。啊！这更难训练了。更好的选择是，激活函数不是二元的，可以表达“50%激活”、“20%激活”之类的概念。这样，当不止一个神经元激活的时候，你可以找到“激活程度最高”的神经元（其实比max更优的选择是softmax，不过目前我们就用max吧）。

当然，如果不止1个神经元表示“100%激活”了，问题仍然存在。不过，由于输出存在中间值，因此学习过程将更平滑、更容易（较少波动），不止1个神经元100%激活的概率要比使用阶跃函数训练小很多（当然，这也取决于训练的数据）。

好，所以我们希望输出中间（模拟）激活值，而不是仅仅输出“激活”或“不激活”（二元值）。

我们第一个想到的是线性函数。

线性函数

A = cx

以上是一个直线函数，激活与函数输入（神经元的加权和）成比例。

所以这将给出一定范围内的激活，而不是二元激活。我们当然可以连接若干神经元，如果不止一个神经元激活了，我们可以基于最大值（max或softmax）做决定。所以这很好。那么，这有什么问题呢？

如果你熟悉用于训练的梯度下降，你会注意到这个函数的导数是一个常数。

A = cx对x的导数是c。这意味着梯度与x无关。这将是一个常数梯度。如果预测出现了错误，反向传播进行的改动将是常数，而不依赖于输入delta(x)！！！

这可不怎么好！（并非总是如此，但请容许我这么说。）此外，还有一个问题。想想连接起来的层。每个层由线性函数激活。这个激活接着作为下一层的输入，下一层同样基于线性函数激活，重复此过程，一直到最后一层。

不管我们有多少层，如果这些层的激活函数都是线性的，最后一层的最终激活函数将是第一层的输入的线性函数！停顿一会，想想这个。

这意味着，这两层（或N层）可以被一个单独的层替换。啊！我们刚刚失去了堆叠网络层的能力。不管我们堆叠多少层，整个网络始终等价于带线性激活的单层神经网络（线性函数的线性组合仍然是一个线性函数）。

让我们继续吧。

sigmoid函数

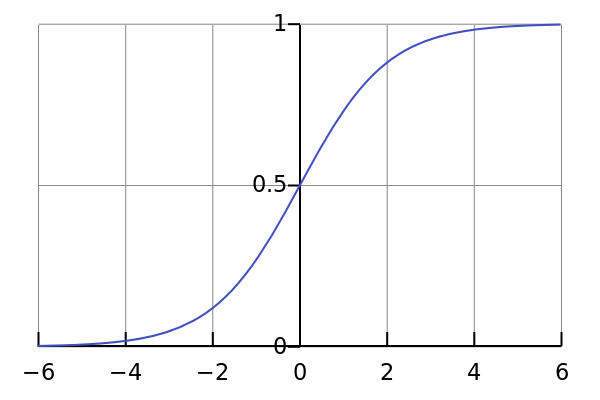
好吧，这曲线看上去很平滑，有点像阶跃函数。那这有什么好处呢？花点时间想一想。

首先，它是非线性的。这意味着该函数的组合也是非线性的。太棒了！我们可以堆叠网络层了。至于非线性激活？是的，它是非线性激活！和阶跃函数不同，它将给出模拟激活。同时，它也具备平滑的梯度。

不知道你注意到了没有，当X位于-2和2之间时，Y的值非常陡峭。这意味着，此区间内X的任意微小变动都将导致Y显著变动。这意味着，该函数趋向于将Y的值导向曲线的两端。

看起来这个性质对分类器而言很有用？没错！确实是这样。它趋向于将激活导向曲线的两边。这在预测上形成了清晰的差别。

另外一个优势是，相对于线性函数(-inf, inf)的值域，该函数的值域为(0, 1)。因此我们的激活函数是有界的。

sigmoid函数是现在使用这广泛的函数之一。那么，它有什么问题呢？

不知道你注意到了没有，越是接近sigmoid的两端，相对X的改变，Y就越趋向于作出非常小的反应。这意味着在该区域的梯度会很小。也就是“衰减的梯度”问题 。嗯，所以当激活函数接近曲线两端的“邻近地平线”部分时发生了什么？

梯度会很小，或者消失了（由于值极小，无法做出显著的改变了）。网络拒绝进一步学习，或者学习速度剧烈地变慢了（取决于具体案例，直到梯度/计算碰到了浮点值的限制）。不过，我们有一些变通措施，因此在分类问题中，sigmoid仍旧非常流行。

Tanh函数

另一个常用的激活函数是tanh函数。

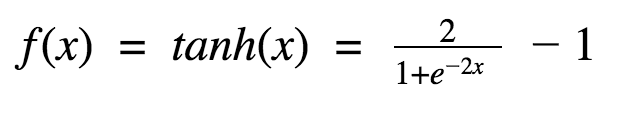
嗯，这看起来和sigmoid很像嘛。实际上，这是一个经过拉升的sigmoid函数！

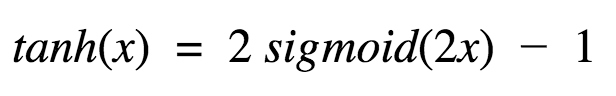
好，tanh的性质和我们之前讨论的sigmoid类似。它是非线性的，因此我们可以堆叠网络层。它是有界的(-1, 1)，所以不用担心激活膨胀。值得一提的是，tanh的梯度比sigmoid更激烈（导数更陡峭）。因此，选择sigmoid还是tanh将取决于你对梯度强度的需求。和sigmoid类似，tanh也存在梯度衰减问题。

tanh也是一个非常流行和广泛使用的激活函数。

ReLu

接着，是ReLu函数，

A(x) = max(0, x)

ReLu函数如上所示。当x是正值时，它输出x，否则输出0。

乍看起来这和线性函数有一样的问题，因为在正值处它是线性的。首先，RuLu是非线性的。ReLu的组合也是非线性的！（实际上它是一个很好的逼近子。ReLu的组合可以逼近任何函数。）很好，这意味着我们可以堆叠网络层。不过，它并不是有界的。ReLu的值域是[0, inf)。这意味着它将膨胀激活函数。

我想指出的另一点是激活的稀疏性。想象一个具有很多神经元的大型神经网络。使用sigmoid或tanh会导致几乎所有神经元以模拟的方式激活（没忘吧？）这意味着需要处理几乎所有的激活以描述网络的输出。换句话说，激活是密集的。这样成本很高。理想情况下，我们希望网络中的一些神经元不激活，从而使激活变得稀疏和高效。

ReLu在这方面很有用。想象一个具备随机初始权重（或归一化的权重）的网络，基于ReLu的特性（x的负值将输出0），基本上50%的网络将生成0。这意味着更少的神经元将被激活（稀疏激活），网络也更轻量。哇，棒！ReLu看起来真不错！是的，它确实不错，但没什么东西不存在缺陷……甚至是RuLu。

ReLu的水平线部分（X的负值）意味着梯度会趋向于0。当激活位于ReLu的水平区域时，梯度会是0，导致权重无法随着梯度而调整。这意味着，陷入此状态的神经元将停止对误差/输入作出反应（很简单，因为梯度是0，没有什么改变）。这被称为死亡ReLu问题。这一问题会导致一些神经元直接死亡、失去响应，导致网络的很大一部分进入被动状态。有一些缓和这一问题的ReLu变体，将水平线转为非水平部分，例如，当x<0时y = 0.01x，使图像从水平线变为略微倾斜的直线。这就是弱修正ReLu（leaky ReLu）。还有其他一些变体。主要的想法是让梯度不为零，这样网络可以逐渐从训练中恢复。

相比tanh和sigmoid，ReLu在算力上更经济，因为它使用的是比较简单的数学运算。设计深度神经网络的时候，这是需要考虑的一个重要因素。

好，该选哪个呢？

现在来考虑该用哪个激活函数的问题。我们是否应该总是使用ReLu呢？还是sigmoid或tanh？好，是也不是。当我们知道尝试逼近的函数具有某些特定性质时，我们可以选择能够更快逼近函数的激活函数，从而加快训练过程。例如，sigmoid对分类器而言很有效（看看sigmoid的图像，是不是展示了一个理想的分类器的性质？），因为基于sigmoid的组合逼近的分类函数要比诸如ReLu之类的函数更容易。当然，你也可以使用自己定制的函数！如果你并不清楚试图学习的函数的本质，那我会建议你从ReLu开始，然后再试其他。在大多数情况下，ReLu作为一个通用的逼近子效果很不错。

在本文中，我尝试描述了一些常用的激活函数。还有其他的激活函数，但基本的思想是一样的。寻找更好的激活函数的研究仍在进行。希望你理解了激活函数背后的思想，为什么要使用激活函数，以及如何选用激活函数。