Buck变换器小信号模型_Buck电路电感电流连续时的小信号模型

本文为大家介绍Buck电路电感电流连续时的小信号模型。

Buck电路电感电流连续时的小信号模型

图1为典型的Buck电路，为了简化分析，假定功率开关管S和D为理想开关，滤波电感L为理想电感（电阻为0），电路工作在连续电流模式（CCM）下。Re为滤波电容C的等效串联电阻，R0为负栽电阻。各状态变量的正方向定义如下图中所示。

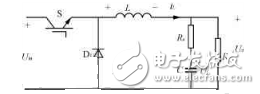
图1 典型buck电路

s导通时，对电感列状态方程

s断开时，D1续流导通时，状态方程变成

占空比为D时，一个开关周期过程中，式（1）及式（2）分别持续了DTs和（1-D）Ts的时间（Ts为开关周期），因此，一个周期内电感的平均状态方程为

稳态时，7=0，则DUin=Uo。这说明稳态时输出电压是一个常数，其大小与占空比D和输入电压Uin成正比。

由于电路各状态变量总是围绕稳态值波动，因此，由式（3）得

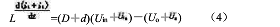
式（4）由式（3）的稳态值加小信号波动值形成。上标为波浪符的量为波动量，d为D的波动量。式（4）减式（3）并略去了两个波动量的乘积项得

由图1，又有

式（6）及式（7）不论电路工作在哪种状态均成立。由式（6）及式（7）可得

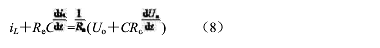
式（8）的推导中假设Re《《R。由于稳态时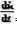=0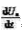，=0，由式（8）得稳态方程为iL=Uo/Rg。

这说明稳态时电感电流平均值全部流过负载。对式（8）中各变量附加小信号波动量得

将式（10）进行拉氏变换得

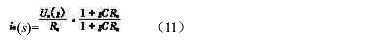
一般认为在开关频率范围内输入电压是恒定的，即可假设Us=0并将其代入式（5），将式（5）进行拉氏变换得

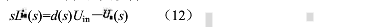
由式（11），式（12）得

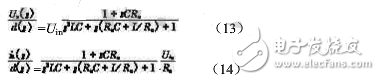
式（13），式（14）便为Buck电路在电感电流连续时的控制—输出小信号传递函数。