

小波软阈值的推导_软阈值的计算
模拟技术
描述
1、小波软阈值的基本原理
小波分解的基本方法是利用Mallat塔式算法,对信号f(x)进行降阶分解,分解过程如图1所示(一般令C0=f(x))。
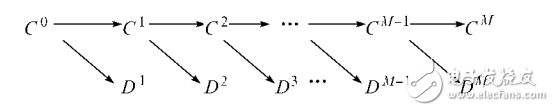
图1 小波分解算法示意图
小波分解算法在每一尺度i下都将信号分解成概貌分量Ci和细节分量Di,在更高一级小波分解中,又将上一级的概貌分量Ci分解成频率成分更低的概貌分量Ci+1和细节分量Di+1。概貌分量Ci主要包含了信号中的低频成分;细节分量Di只包含信号的高频部分,其中也包括高频噪声。由前所述,噪声的小波变换系数随尺度的增大而减小,连续信号的小波系数随尺度的增大而增大。这样可以设定一阈值,利用该阈值按照一定的规则对小波系数进行阈值调整。对经阈值调整后的各级小波系数按小波变换的反演算法进行信号重构,得到消噪后的信号。
由于噪声信号强度的随机性,以及小波分解过程中信号与噪声的传播特性不同,每一层小波分解系数所采用的阈值应该是随小波系数的变化而变化的。能实现这种变动阈值的方法就是软阈值去噪方法。
2、软阈值的计算
设被检测的信号为:

软阈值的计算方法很多。经比较,本文的软阈值计算采用试探法的Stein无偏风险阈值计算方法,它是在通用阈值和无偏风险阈值的基础上进行计算的。具体计算原理和计算步骤如下。
a.噪声强度的计算
噪声强度的计算可采用以下公式:
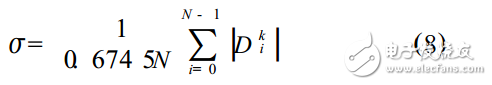
式中:Dki为第k层小波系数(1《k《M);N为该层小波系数的个数;M为小波分解最高次数(参见图1)。
b.通用阈值的计算
通用阈值计算的理论依据是:N个具有独立同分布的标准高斯变量中的最大值小于T1的概率随着N的增大而趋于1。其中,T1由下式来计算:
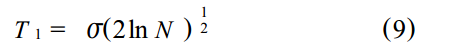
式中:R为噪声强度;N为所处理的变量的个数。
c.Stein无偏风险阈值的计算
将某一层小波系数的平方按由小到大排列,得到一个向量:W=[w1,w2,…,wN],其中w1≤w2≤…≤wN,N为小波系数的个数。由此计算风险向量R=[r1,r2,…,rN],其中:
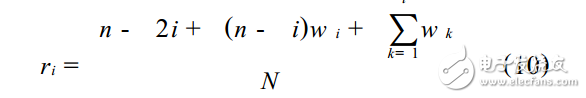
以R元素中的最小值rb作为风险值,由rb的下标变量b求出对应的wb,则阈值T2为:

d.试探法的Stein无偏风险阈值的计算

最终的软阈值就是T3。
软阈值算法的意义不仅在于实现信号去噪、检测,对数据压缩也有贡献。如:采样频率为6400Hz时,每一基波周期中,C0有128个数据,经小波分解后,C1和D1各有64个数据;而经软阈值消噪处理后,D1中仅有6个~15个点的数值非零。这样,数据被大大压缩,数据存储量和传输效率提高了。
-
小波去噪阈值如何选取_小波阈值分析2018-01-10 62008
-
基于EEMD和模糊阈值的去噪方法2017-11-21 1235
-
压缩感知的冗余字典及其迭代软阈值实现算法2017-01-07 892
-
GIS局部放电小波阈值去噪算法的改进2015-12-18 955
-
小波阈值去噪改进算法研究2011-06-22 1152
-
GPS观测数据的小波阈值法去噪2011-05-30 1071
-
基于一种新阈值函数的小波医学图像去噪2010-01-15 850
-
波原子纹理图像阈值算法2009-11-11 773
-
一种改进的小波阈值降噪方法性能分析2009-08-14 673
全部0条评论

快来发表一下你的评论吧 !

