

小波去噪的优点与不足_小波去噪方法的分析比较
模拟技术
描述
小波分析是近十几年来发展起来的一种新的数学理论和方法,目前已被成功地应用于许多领域。作为一种新的时频分析方法,小波分析由于具有多分辨分析的特点,能够聚焦到信号的任意细节进行多分辨率的时频域分析,因而被誉为“数学显微镜”。
本文主要介绍小波分解与重构法、非线性小波变换阈值法、平移不变量小波法以及小波变换模极大值法这4种常用的小波去噪方法。将它们分别用于仿真算例的去噪处理,并对这几种方法的应用场合、去噪性能、计算速度和影响因素等方面进行比较,最后对小波去噪方法选择加以总结。
1、小波分解与重构法去噪
本质上相当于一个具有多个通道的带通滤波器,主要适用于有用信号和噪声的频带相互分离时的确定性噪声的情况。在这种情况下,该方法能基本去除噪声,去噪效果很好。但对于有用信号和噪声的频带相互重叠的情况(如信号混有白噪声),效果就不甚理想。
优点:
适用范围不是很广泛。它对于特定情况下已知道噪声的频率范围且信号和噪声的频带相互分离时非常有效。对实际应用中广泛存在的白噪声,其去噪效果则较差。
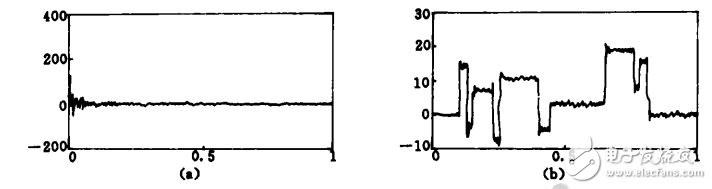
图1 小波分解与重构法去噪
2、非线性小波变换阈值法去噪
主要适用于信号中混有白噪声的情况。用阈值法去噪的优点是噪声几乎完全得到抑制,且反映原始信号的特征尖峰点得到很好的保留。用软阈值的方法去噪能够使估计信号实现最大均方误差最小化,即去噪后的估计信号是原始信号的近似最优估计;且估计信号至少和原始信号同样光滑而不会产生附加振荡。
该方法还具有广泛的适应性,因而是众多小波去噪方法中应用最为广泛的一种。阈值法的计算速度很快,为O(N),其中N为信号长度。
在有些情况下,如在信号的不连续点处,去噪后会出现伪吉布斯现象。且用该方法去噪时,阈值的选择对去噪效果有着很重要的影响。

图2 软阈值法去噪
3、平移不变量小波法去噪
主要适用于信号中混有白噪声且含有若干不连续点的情况,是在阈值法基础上的改进。
可以有效地去除阈值法去噪中,在信号的不连续点处所产生的伪吉布斯现象,表现出比阈值法更好的视觉效果。从L2范数误差的观点看,经该方法去噪能够得到比阈值法更小的均方根误差,信噪比也得到一定地提高;
计算速度没有阈值法快。当信号长度是N时,计算速度是O(NlogN)。
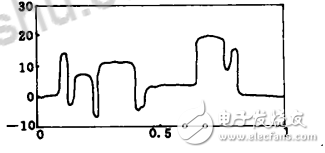
图3 平移不变量小波法去噪
4、模极大值法去噪
主要适用于信号中混有白噪声,且信号中含有较多奇异点的情况。
该方法在去噪的同时,有效地保留信号的奇异点信息,去噪后的信号没有多余振荡,是原始信号的一个非常好的估计,具有较好的图面质量。
用模极大值进行重构时采用的是交替投影法,为保证重构信号的精度,提高信噪比,通常要进行几十次的迭代,每迭代一次的速度是O(NlogN)。因此,计算速度非常慢,通常要比前几种方法慢数十倍。
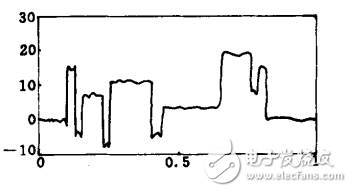
图4 小波变换模极大值法去噪
通过对几种小波去噪方法的分析比较,总结出如下几点,可以为小波去噪方法的选择提供参考依据。
(1)对于信号和噪声的频带相互分离的确定性噪声的去噪处理,选用方法简单、算速度快的小波分解与重构去噪法最为合适。
(2)对于高斯白噪声的去噪处理,可以选用阈值法、平移不变量法以及模极大值法。究竟选择哪种方法应根据实际信号的特点以及这几种方法的优缺点再作决定。①阈值法由于具有能得到原始信号的
近似最优估计、计算速度快以及具有广泛的适应性等优点,是小波去噪方法中应用最广泛的一种。一般情况下,均可选用该方法去噪。②平移不变量法适用于信号中含有若干不连续点的情况。通常去噪性能优于阈值法,但以牺牲计算速度为代价。③小波变换模极大值法当信号中含有较多奇异点时去噪性能相当好,但其最大缺点就是计算速度太慢,在应用中需权衡去噪效果和计算速度之间的关系。
(3)小波去噪方法和其它方法结合使用,可能会达到更好的效果
全部0条评论

快来发表一下你的评论吧 !

