

matlab小波去噪函数实例
嵌入式设计应用
描述
[xd,cxd,lxd]=wden(x,tptr,sorh,scal,n,‘wname’)
式中:输入参数x为需要去噪的信号;
1.tptr:阈值选择标准。
1)无偏似然估计(rigrsure)原则。它是一种基于史坦无偏似然估计(二次方程)原理的自适应阈值选择。对于一个给定的阈值t,得到它的似然估计,再将似然t最小化,就得到了所选的阈值,它是一种软件阈值估计器。
2)固定阈值(sqtwolog)原则。固定阈值thr2的计算公式为:thr2log(n)2=(6)式中,n为信号x(k)的长度。
3)启发式阈值(heursure)原则。它是rigrsure原则和sqtwolog原则的折中。如果信噪比很小,按rigrsure原则处理的信号噪声较大,这时采用sqtwolog原则。
4)极值阈值(minimaxi)原则。它采用极大极小原理选择阈值,产生一个最小均方误差的极值,而不是没有误差。
2、sorh:阈值函数选择方式,即软阈值(s)或硬阈值(h)。
3.scal:阈值处理随噪声水平的变化,scal=one表示不随噪声水平变化,scal=sln表示根据第一层小波分解的噪声水平估计进行调整,scal=mln表示根据每一层小波分解的噪声水平估计进行调整。
4.n和wname表示利用名为wname的小波对信号进行n层分解。输出去噪后的数据xd及xd的附加小波分解结构[cxd,lxd]。
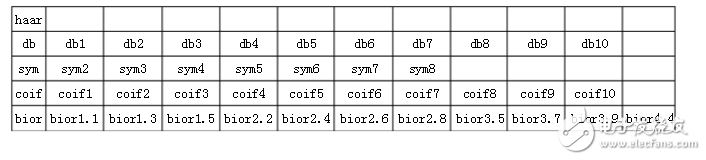
常见的几种小波:haar,db,sym,coif,bior
用MATLAB对一语音信号进行小波分解,分别用强阈值,软阈值,默认阈植进行消噪处理。
代码:
%装载采集的信号leleccum.mat
loadleleccum;
%=============================
%将信号中第2000到第3450个采样点赋给s
indx=2000:3450;
s=leleccum(indx);
%=============================%画出原始信号
subplot(2,2,1);
plot(s);
title(‘原始信号’);
%=============================
%用db1小波对原始信号进行3层分解并提取系数
[c,l]=wavedec(s,3,‘db1’);
a3=appcoef(c,l,‘db1’,3);
d3=detcoef(c,l,3);
d2=detcoef(c,l,2);
d1=detcoef(c,l,1);
%=============================
%对信号进行强制性消噪处理并图示结果
dd3=zeros(1,length(d3));
dd2=zeros(1,length(d2));
dd1=zeros(1,length(d1));
c1=[a3dd3dd2dd1];
s1=waverec(c1,l,‘db1’);
subplot(2,2,2);
plot(s1);grid;
title(‘强制消噪后的信号’);
%=============================
%用默认阈值对信号进行消噪处理并图示结果
%用ddencmp函数获得信号的默认阈值
[thr,sorh,keepapp]=ddencmp(‘den’,‘wv’,s);
s2=wdencmp(‘gbl’,c,l,‘db1’,3,thr,sorh,keepapp);
subplot(2,2,3);
plot(s2);grid;
title(‘默认阈值消噪后的信号’);
%=============================
%用给定的软阈值进行消噪处理
sosoftd2=wthresh(d2,‘s’,1.823);
softd3=wthresh(d3,‘s’,2.768);
c2=[a3softd3softd2softd1];
s3=waverec(c2,l,‘db1’);
subplot(2,2,4);
plot(s3);grid;
title(‘给定软阈值消噪后的信号’);
ftd1=wthresh(d1,‘s’,1.465);
-
【案例分享】LabVIEW和Matlab混合编程的小波去噪方法2019-08-06 4432
-
基于新阈值函数的小波阈值去噪算法2018-01-10 10765
-
基于LabVIEW和Matlab混合编程的小波去噪方法2015-01-16 11988
-
labview中调用matlab script节点做小波去噪分析2014-03-05 5445
-
基于LabVIEW与MATLAB的心音检测与小波去噪2010-10-18 587
-
基于一种新阈值函数的小波医学图像去噪2010-01-15 848
全部0条评论

快来发表一下你的评论吧 !

