

小波变换原理与应用_小波变换的基本原理_小波变换的应用
嵌入式操作系统
描述
小波变换(wavelet transform,WT)是一种新的变换分析方法,它继承和发展了短时傅立叶变换局部化的思想,同时又克服了窗口大小不随频率变化等缺点,能够提供一个随频率改变的“时间-频率”窗口,是进行信号时频分析和处理的理想工具。
它的主要特点是通过变换能够充分突出问题某些方面的特征,能对时间(空间)频率的局部化分析,通过伸缩平移运算对信号(函数)逐步进行多尺度细化,最终达到高频处时间细分,低频处频率细分,能自动适应时频信号分析的要求,从而可聚焦到信号的任意细节,解决了Fourier变换的困难问题,成为继Fourier变换以来在科学方法上的重大突破。
小波变换的基本原理
传统的信号理论,是建立在Fourier分析基础上的,而Fourier变换作为一种全局性的变化,其有一定的局限性。在实际应用中人们开始对Fourier变换进行各种改进,小波分析由此产生了。小波分析是一种新兴的数学分支,它是泛函数、Fourier分析、调和分析、数值分析的最完美的结晶;在应用领域,特别是在信号处理、图像处理、语音处理以及众多非线性科学领域,它被认为是继Fourier分析之后的又一有效的时频分析方法。
小波变换与Fourier变换相比,是一个时间和频域的局域变换因而能有效地从信号中提取信息,通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析(Multiscale Analysis),解决了Fourier变换不能解决的许多困难问题。
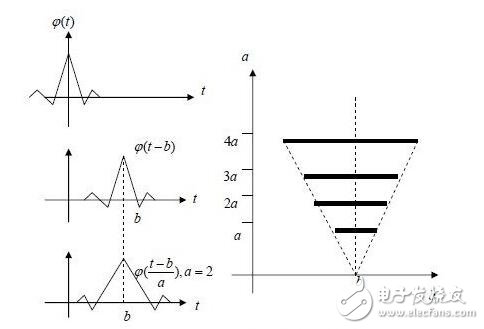
小波变换的应用
小波是多分辨率理论的分析基础。而多分辨率理论与多种分辨率下的信号表示和分析有关,其优势很明显--某种分辨率下无法发现的特性在另一个分辨率下将很容易被发现。从多分辨率的角度来审视小波变换,虽然解释小波变换的方式有很多,但这种方式能简化数学和物理的解释过程。
对于小波的应用很多,我学习的的方向主要是图像处理,所以这里用图像的应用来举例。对于图像,要知道量化级数决定了图像的分辨率,量化级数越高,图像越是清晰,图像的分辨率就高。
一、小波地位
小波曾火热一时,但小波不是万能的,在某些应用场合特别适用 小波无法求解微分方程纯数字和物理地位不如FT
二、信号检测方面应用 发动机声音中的撞击声检测
傅里叶分析:时间平均作用模糊了信号局部特性 Gabor变换 :仍需长窗去包含振荡波形 小波变换 : 小波基可任意窄
三、降噪应用
1、适用场合
经典滤波:要求信号与噪声频率足够窄且不重合
高斯类噪声和脉冲噪声——宽带噪声——小波去噪
2、滤波效果
①经典滤波:丢失波形尖锐处信息
②小波降噪:基本保留波形尖锐处信息(与小波基选择有关)
3、滤波手段
①传统方法:Prony参数建模法
②小波降噪
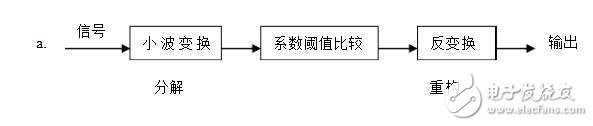
b、可证明其统计最优性
c、阈值比较(阈值T可基于信号标准差得出)
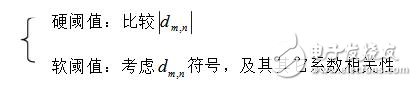
4、小波基选择:小波基应与主体信号量相近相似度越高,主小波系数越大,噪声系数则越小——NI信号处理工具箱
- 相关推荐
- 热点推荐
- 小波变换
-
小波变换与傅里叶变换的区别和联系2023-09-07 4467
-
了解小波变换针对傅立叶变换的优点2020-05-07 6280
-
如何使用LabVIEW实现小波变换2020-04-20 2331
-
详解傅里叶变换与小波变换2018-01-16 1247
-
小波变换比傅里叶变换好在哪里_小波变换与傅里叶变换详解2018-01-13 16744
-
基于Multisim的三角波变换成锯齿波,就是输入三角波信号经过波形变换器后变换成锯齿波信号?2017-05-08 10992
-
基于变分和小波变换的图像放大算法2015-11-24 703
-
小波变换在符号率估计中的应用研究2012-02-07 682
-
基于小波变换的信号滤波和去噪研究2011-08-03 1334
-
基于小波变换的QRS波检测算法2011-01-07 592
-
基于提升小波变换的SPECK图像编码算法2010-01-01 679
-
一个基于C语言的小波变换的图像压缩方案2009-09-11 705
-
小波变换工程分析与应用 --杨福生2009-04-23 1199
全部0条评论

快来发表一下你的评论吧 !

