隐马尔科夫模型详解分析

观察序列生成

计算观察序列的概率（Finding the probability of an observed sequence）

给定隐马尔科夫模型，也就是在模型参数（pi， A， B）已知的情况下，我们想找到观察序列的概率。还是考虑天气这个例子，我们有一个用来描述天气及与它密切相关的海藻湿度状态的隐马尔科夫模型（HMM），另外我们还有一个海藻的湿度状态观察序列。假设连续3天海藻湿度的观察结果是（干燥、湿润、湿透）——而这三天每一天都可能是晴天、多云或下雨，对于观察序列以及隐藏的状态，可以将其视为网格：

网格中的每一列都显示了可能的的天气状态，并且每一列中的每个状态都与相邻列中的每一个状态相连。而其状态间的转移都由状态转移矩阵提供一个概率。在每一列下面都是某个时间点上的观察状态，给定任一个隐藏状态所得到的观察状态的概率由混淆矩阵提供。

穷举搜索（ Exhaustive search for solution）

可以看出，一种计算观察序列概率的方法是找到每一个可能的隐藏状态，并且将这些隐藏状态下的观察序列概率相加。对于上面那个（天气）例子，将有3^3 = 27种不同的天气序列可能性，因此，观察序列的概率是：

Pr（dry，damp，soggy | HMM） = Pr（dry，damp，soggy | sunny，sunny，sunny） + Pr（dry，damp，soggy | sunny，sunny ，cloudy） + Pr（dry，damp，soggy | sunny，sunny ，rainy） + 。 。 。 。 Pr（dry，damp，soggy | rainy，rainy ，rainy）

用这种方式计算观察序列概率极为昂贵，特别对于大的模型或较长的序列，因此我们可以利用这些概率的时间不变性来减少问题的复杂度。

前向算法

给定模型，求某个观察序列O的概率（样例问题2）。［HMM：隐马尔科夫模型 - 学习 ］

对于这个基本问题，计算公式为：

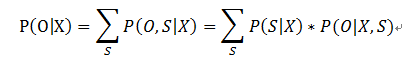
即对于观察序列O，我们需要找出所有可能的隐藏状态序列S，计算出在给定模型下S输出为O的概率（就是样例问题一啊），然后计算概率之和。

直观上看，假如序列O的长度为T，模型的隐藏状态集合大小为N，那么一共有NT个可能的隐藏状态序列，计算复杂度极高O（NT），暴力算法太慢了。

解决方案就是动态规划（Dynamic Programming）。

假设观察序列为O1，O2，O3，…。，Ot. 在时刻i（1《i《=t）时，定义C为产生序列O1，O2，…，Oi且Si=Sk的概率：

其中，Sk为任意一个隐藏状态值。

则C（i+1，Or）的计算公式为：

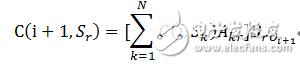
其中，Sr为任意一个隐藏状态值。A为转移概率。B为隐藏状态到观察状态的概率。为了便于理解，还是看图：

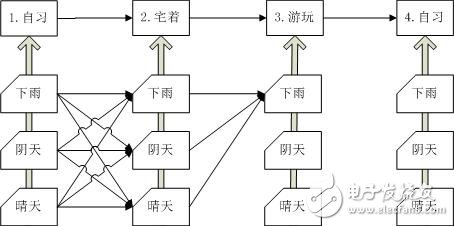
C（3，下雨）考虑了t=1和t=2的所有组合情况，同时也是C（4，下雨|阴天|晴天）的子问题。C（3，阴天）和C（3，晴天）也是如此计算，而C（i+1，Sr）计算公式则可以表示成：

由图知：C（4，阴天）=［C（3，下雨）*A（下雨，阴天）+C（3，阴天）*A（阴天，阴天）+C（3，晴天）*A（晴天，阴天）］*B（阴天，自习）。

预测分布

观 测 数 据 是 X = {x 1 ， 。 。 。 ， x N } ， 我 们 希 望 预测 x N +1 ，这对于诸如金融预测这种实时的应用来说很重要。

首先运行前向 α 递归然后计算最后一个式子中关于 z N 和 z N +1 的求和式的方式得到。

第一项关于 z N 的求和式可以被存储起来，一旦 x N +1 被观测到，就可以用来运行 α 递归的前向步骤，进行到下一步，来预测接下来的值 x N +2 。注意，在式中，从 x 1 和 x N 的所有数据的影响被聚集到了 α（z N ） 的 K 个值当中。因此预测分布可以使用固定量的存储空间向前推进无穷多次，这正是实时应用所要求的。

某小皮

维特比算法 Viterbi Algorithm

目标-解决HMM的基本问题之二（解码问题）：给定观察序列以及模型（参数），如何选择一个对应的状态序列S，使得S能够最为合理的解释观察序列？即寻找最可能的隐藏状态序列（Finding most probable sequence of hidden states），寻找概率最高的隐含状态序列。

近似算法

近似算法的想法是：在每个时刻t选择在该时刻最有可能出现的状态it*，从而得到一个状态序列I* = （i1*，i2*， 。。.， iT*），将它作为预测的结果。即寻找分别概率最高的状态的集合。

近似算法计算简单。然而，通常这样的状态集合不会对应于最可能的状态序列。事实上，如果对于两个连续的状态，它们单独的概率都是最高的，但是连接它们的转移矩阵的元素为零，那么这个状态集合表示一个具有零概率的序列。

给定隐马尔可夫模型λ和观测序列O，在时刻t处于状态qi的概率γt（i）是

在每一时刻t最有可能的状态it*是

从而得到状态序列I* =（i1*， i2*， 。。.， iT*）。

暴力算法

计算所有可能性的概率，然后找出拥有最大概率值的隐藏状态序列。复杂度为O（NT）。

维特比算法（基于前向算法的动态规划）

根据动态规划原理，最优路径具有这样的特征：如果最优路径在时刻t通过节点it*，那么这一路径中“从节点i1*到终点it*的部分路径”对于“从节点i1*到终点it*的所有可能的部分路径”来说必须是最优的。

首先导入两个变量δ和ψ。定义在时刻t状态为i的所有单个路径（i1， i2， 。。.， it）中概率最大值为：

由定义可得变量δ的递推公式：

定义在时刻t状态为i的所有单个路径（i1，i2， 。。. ， it-1， it）中概率最大的路径的第t-1个节点为

算法（维特比算法）

输入：模型λ= （A， B，π）和观测O=（o1，o2， 。。.， oT）；

输出：最优路径I* = （i1*，i2*， 。。.， iT*）。

过程：

Note： 最大加和算法作用于对数概率，因此无需使用前向后向算法中的重新缩放的变量。

维特比算法示例

考虑盒子和球模型λ=（A， B，π），状态集合Q={1， 2， 3}，观测集合V={红， 白}，

已知观测序列O=（红，白，红），试求最优状态序列，即最优路径I* = （i1*， i2*， i3*）。

求最优路径

求得最优路径，即最有状态序列I* = （i1*， i2*， i3*）= （3， 3， 3）。