

点电荷的电势公式的推导_点电荷的电势分布公式
电气技术
描述
什么是电势
静电场的标势称为电势,或称为静电势。在电场中,某点电荷的电势能跟它所带的电荷量(与正负有关,计算时将电势能和电荷的正负都带入即可判断该点电势大小及正负)之比,叫做这点的电势(也可称电位),通常用φ来表示。电势是从能量角度上描述电场的物理量。(电场强度则是从力的角度描述电场)。电势差能在闭合电路中产生电流(当电势差相当大时,空气等绝缘体也会变为导体)。电势也被称为电位。
定理定律
在静电学里,电势(electric potential)(又称为电位)定义为:处于电场中某个位置的单位电荷所具有的电势能。电势只有大小,没有方向,是标量,其数值不具有绝对意义,只具有相对意义。
(1)单位正电荷由电场中某点A移到参考点O(即零势能点,一般取无限远处或者大地为零势能点)时电场力做的功与其所带电量的比值。
所以φA=Ep/q。在国际单位制中的单位是伏特(V)。
(2)电场中某点相对参考点O电势的差,叫该点的电势。
“电场中某点的电势在数值上等于单位正电荷在那一点所具有的电势能”。
公式:ε=qφ(其中ε为电势能,q为电荷量,φ为电势),即φ=ε/q
在电场中,某点的电荷所具的电势能跟它的所带的电荷量之比是一个常数,它是一个与电荷本身无关的物理量,它与电荷存在与否无关,是由电场本身的性质决定的物理量。
电势是描述静电场的一种标量场。静电场的基本性质是它对放于其中的电荷有作用力,因此在静电场中移动电荷,静电场力要做功。但静电场中沿任意路径移动电荷一周回到原来的位置,电场力所做的功恒为零,即静电场力做功与路径无关,或静电场强的环路积分恒为零。[1]
静电场的这一性质称为静电场的环路定理。根据静电场的这一性质可引入电势来描述电场,就好像在重力场中重力做功与路径无关,可引入重力势描述重力场一样。电场中某一点的电势定义为把单位正电荷从该点移动到电势为零的点,电场力所做的功。通常选择无限远点的电势为零,因此某点的电势就等于把单位正电荷从该点移动到无限远,电场力所做的功,表示为:
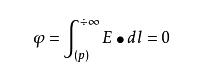
电势的单位为V(伏),1V=1J/C(1焦/库)。静电场中电势相等的点构成一些曲面,这些曲面称为等势面。电力线总是与等势面正交,并指向电势降低的方向,因此静电场中等势面的分布就绘出了电场分布。电势虽然是引入描述电场的一个辅助量,但它是标量,运算比矢量运算简单,许多具体问题中往往先计算电势,再通过电势与场强的关系求出场强。电路问题中电势和电势压(即电压)是一个很有用的概念。电势是普遍描述电场的电磁势的特例。
应用领域
(1) 热噪声在超导结中引起的静电势的多次增加和多次减少: 研究人员研究了在过阻尼和欠阻尼两种情况下、在考虑了热噪声和有交流信号和直流信号同时输入的情况下的超导结两端的静电势。研究表明,随着温度的增加(热噪声的强度和温度成正比),静电势会多次被增加和多次被减小 (静电势多次被增加的峰值对应于静电势的共振激活现象)。另外,超导结两端的静电势还表现出(噪声引起的) 热噪声加强稳定的现象。
(2) 耦合超导结系统(或器件)中时空噪声的出现和其对输运的影响: 在该研究中,研究人员首次发现了时空噪声可能出现在耦合超导结系统(一个超导量子干涉器件)中,并且时空噪声与电子对的波函数的相差的关联所引起的系统的对称破缺能够引起输运。通过对两个模型(一个高斯噪声模型和一个电报噪声模型)的研究,研究人员发现在所研究的耦合超导结系统中几率流总是负的并且随着热噪声强度的增加而会出现一个“井”。根据研究人员的研究结果,研究人员可以控制噪声使几率流处于有利于科研人员的实验要求的状态。比如,如果研究人员希望在实验中得到较大的负几率流时,研究人员可以采取下面的两个措施:a)。 在一定的环境扰动下,我们可以适当地调整温度使负几率流处于上面所提到的“井” 的附近 (热噪声的强度与温度成正比)以便于得到有利于我们实验要求的结果;b)。 在一定的温度下,研究人员们应当采取一定的措施来调节环境扰动以便使负几率流的绝对值尽可能地大。
(3) 一个热-惯性“ratchet”超导量子干涉器件(耦合超导结)中的混沌噪声输运:研究了一个热-惯性“ratchets”超导量子干涉器件中在有周期信号的输入的情况下的混沌噪声输运。 研究表明,通过控制温度和外部输入信号的强度,研究人员可以使输运的方向反号。当温度足够低时,研究人员很容易得到混沌输运; 但当温度足够高时,输运主要是热噪声输运。
(4) 环境扰动下的耦合超导结: 研究人员在考虑了内部热涨落和外部环境扰动的情况下研究了一个SQUID[超导量子干涉器件(耦合超导结)],发现外部环境的扰动可在SQUID中引起输运,通过控制内部热涨落和外部环境的扰动之间的关联可使静电势反号;并发现随着系统内部温度的增加,电流—电压特性越来越接近于正常状态下的欧姆定律。
(5) 热涨落和环境扰动的关联可在单个超导结中引起的静电势:它们却在国际上激起了大量科研工作者的研究兴趣。在相关论文中研究人员研究了外部环境的扰动所引起的噪声与内部热涨落的关联在超导结中所引起的静电势。研究表明,系统内部的热涨落和外部环境的扰动之间的关联可以引起对称破缺,从而在超导结中引起静电势。
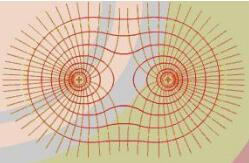
点电荷的电势公式的推导
电荷周围产生的静电场的电势差与电势的公式与推导:
一场源点荷为Q,在距Q为r的A点有一点电荷为q,求证:此A处电势φ=kQ/r 证明:设无穷远处电势为0,则在电场力的作用下,q从r处运动到无穷远,电场力做功为qU.
将A到无穷远这段距离无限等分最远处距离为r0,A 处为rn,(0,1,2,……n为下标)
1、式子:
kQq*(r(n-1)-rn)/rn^2+kQq*(r(n-2)-r(n-1))/r(n-1)^2+……+kQq*(r2-r3)/r3^2+kQq*(r1-r2)/r2^2+kQq*(r0-r1)/r1^2=qU
2、式子:
kQq*(r(n-1)-rn)/(rn*r(n-1))+kQq*(r(n-2)-r(n-1))/(r(n-1)*r(n-2))+……+kQq*(r2-r3)/(r3*r2)+kQq(r1-r2)/(r2*r1)+kQq*(r0-r1)/(r1*r0)=qU
因此
kQ/rn-kQ/r(n-1)+kQ/r(n-1)-kQ/r(n-2)+……+kQ/r3-kQ/r2+kQ/r2-kQ/r1+kQ/r1-kQ/r0=U kQ/rn-kQ/r0=U kQ/rn-0=φ-0 φ=kQ/rn,即φ=kQ/r
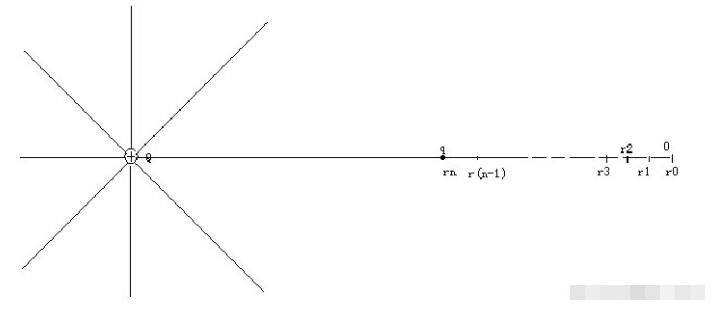
图1 电势公式的推导
点电荷的电势分布公式
1、均匀分布的球面电荷(球面半径为R。带电量为q) 电势分布公式为:
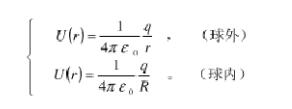
2、均匀分布的球体电荷(球体的半径为R,带电量为q)电势分布公式为:
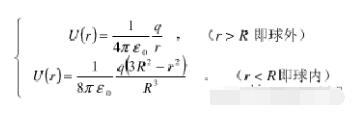
3、均匀分布的无限大平面电荷(电荷面密度为sigma) 电势分布公式为:
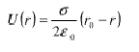
其中假设r0处为零电势参考点。若选取原点为零电势参考点。即U0=0,那么其余处的电势公式为:
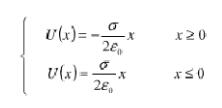
4、均匀分布的无限长圆柱柱面电荷电势分布公式为:
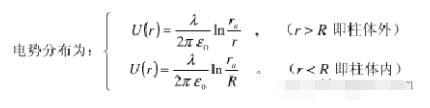
-
负电荷的电势沿电场线降低吗2024-07-29 5527
-
电势能和电势的区别与联系2024-02-26 7742
-
定子绕组电势平衡方程式 转子绕组的电势及电流公式2023-05-31 6159
-
电势能和电势总结2019-08-21 19914
-
判断电势高低的方法_电势的公式介绍2018-03-15 84803
-
点电荷电场中的电场线_点电荷的电场线分布2018-01-22 34999
全部0条评论

快来发表一下你的评论吧 !

