lc正弦波振荡电路详解_LC正弦波振荡电路振荡的判断方法

　　LC正弦波振荡电路与RC桥式正弦波振荡电路的组成原则在本质上是相同的，只是选频网络采用LC电路。在LC振荡电路中，当f=f0时，放大电路的放大倍数数值最大，而其余频率的信号均被衰减到零；引入正反馈后，使反馈电压作为放大电路的输入电压，以维持输出电压，从而形成正弦波振荡。由于LC正弦波振荡电路的振荡频率较高，所以放大电路多采用分立元件电路。

　　正弦波振荡电路详解

　　一个放大电路，在输入端加上输入信号的情况下，输出端才有输出信号。如果输入端无外加输入信号，输出端仍有一定频率和幅度的信号输出，这种现象称为放大电路的自激振荡。振荡电路就是在没有外加输入信号的情况下，依靠电路自激振荡而产生正弦波输出电压的电路。它广泛应用于遥控、通信、自动控制、测量等设备中，也作为模拟电子电路的测试信号。

　　1、产生正弦波振荡的条件

　　图1所示的正弦波振荡电路是一个未加输入信号的正反馈闭环电路。若输出正弦电压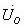经反馈环节产生的反馈电压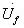恰好等于放大电路所需的输入电压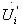（幅度相等、相位相同），即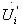=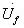，则可在闭环电路输出端得到持续稳定的正弦波，如图1（b）所示。由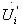=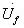，可得

　　

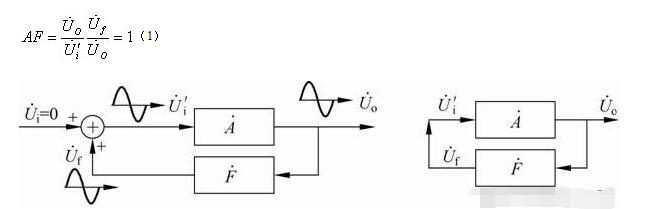
　　图1 正弦波振荡电路的框图

　　式（1）就是产生正弦波振荡的振荡条件。式（1）为复数式，若设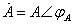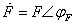，，正弦波振荡条件可用幅度平衡条件和相位平衡条件来表示。

　　幅度平衡条件

　　|AF|=1（2）

　　相位平衡条件

　　（3）

　　2、正弦波振荡的建立和稳定

　　一个实际的正弦波振荡电路的初始信号是由电路内部噪声和瞬态过程的扰动引起的。通常这些噪声和扰动的频谱很宽而幅度很小。为了最终能得到一个稳定的正弦信号，首先，必须用一个选频环节把所需频率的分量从噪声或扰动信号中挑选出来使其满足相位平衡条件，而使其他频率分量不满足相位平衡条件。其次，为了能使振荡能够从小到大建立起来，要求满足

　　|AF|》1（4）

　　式（4）称为正弦波振荡的起振条件。

　　从式（4）可以看到，振荡建立起来后，信号由小到大不断增长，不能得到一个稳定的正弦波。实际上，信号的幅度最终要受到放大电路非线性的限制，即当幅度逐渐增大时，|A|将逐渐减小，最终使|AF|=1达到幅度平衡条件，从而使正弦波振荡稳定。

　　3、正弦波振荡电路的组成

　　从上述分析可知，正弦波振荡电路从组成上看必须有以下四个基本环节。

　　（1）放大电路：保证电路能够由从起振到动态平衡的过程，是电路获得一定幅值的输出量，实现能量的控制。

　　（2）选频网络：确定电路的振荡频率，使电路产生单一频率的振荡，即保证电路产生正弦波振荡。

　　（3）正反馈网络：引入正反馈，使放大电路的输入信号等于反馈信号。

　　（4）稳幅环节：也就是非线性环节，作用是使输出信号幅值稳定。

　　在不少实用电路中，常将选频网络和正反馈网络“合二为一”；而且，对于分立元件放大电路，也不再另加稳幅环节，而依靠晶体管特性的非线性起到稳幅作用。

　　正弦波振荡电路常根据选频网络所用元件来命名，分为RC正弦波振荡电路、LC正弦波振荡电路和石英晶体正弦波振荡电路3种类型。RC正弦波振荡电路振荡频率较低，一般在1MHz以下；LC正弦波振荡电路振荡频率较高，一般在1MHz以上；石英晶体正弦波振荡电路也可以等效为LC正弦波振荡电路，其特点是振荡频率非常稳定。

　　LC正弦波振荡电路振荡的判断方法

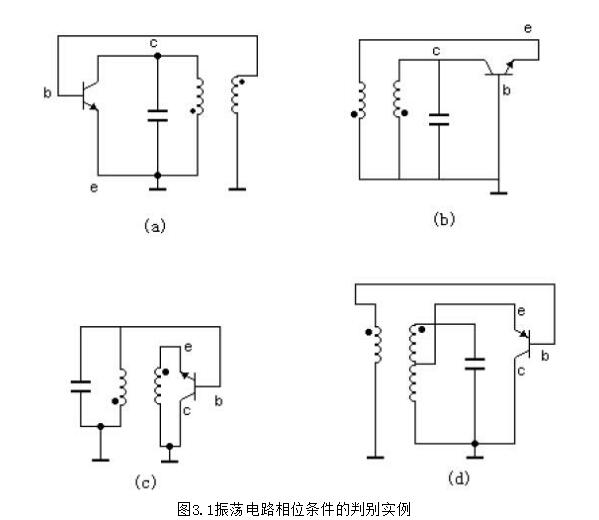
　　采用LC谐振回路作为选频网络的反馈式振荡器称为LC正弦波振荡器。 按照反馈网络的形式来分，LC正弦波振荡器可分为：变压器耦合振荡器、三点式振荡器。针对相位条件，可依据瞬时极性法判定电路中存在的反馈是否是正反馈来加以判别。下面针对LC正弦波振荡电路的具体实例来说明其判定方法。

　　为分析电路的方便，特别提出以下两点说明：

　　1、本文所画的电路图均指振荡电路的交流等效电路；

　　2、假设本文的电路均已满足起振的振幅条件，即只要电路满足起振的相位条件就可振荡。

　　3、变压器耦合振荡器

　　3.1、什么是变压器的同名端

　　在分析具体电路之前，先来介绍一下什么是变压器的同名端。

　　同名端是指在同一交变磁通的作用下，任一时刻两个（或两个以上）绕组中都具有相同电势极性的端头彼此互为同名端。变压器的极性辨别就属于同名端问题。

　　变压器及三相变压器同名端的含义用“•”来表示初、次级绕组感生电动势的相位。初、次级绕组均带“•”的两对应端，表示该两端感生电动势的相位相同，称为同名端。一端带“•”而另一端不带“•”的两对应端，则表示该两端感生电动势相位相反，称为非同名端，亦称为异名端。

　　3.2、 变压器耦合振荡器

　　变压器耦合振荡器是通过变压器的初、次级互感耦合产生反馈电压的，因此，为了满足正反馈条件，必须正确地设置初、次级绕组的同名端。根据晶体管三个电极上输出与输入的相位关系，即射极与基极和集电极与射极为同相关系，而集电极与基极则为反相关系。

　　因此，以射极为准，当变压器初、次级绕组与晶体管相接时，其同名端设置应遵照如下规则：射极相接的绕组端与基极或集电极相接的另一绕组端应为同名端，否则不满足正反馈的条件。这一规则也可以概括为“射基（集）同名”。并且在变压器耦合振荡器的分析中，这种规则可作为判别其是否满足相位条件的依据。

　　下面通过实例来说明其判别方法：

　　在图3.1（a）电路中，发射极相接的绕组端与基极相接的另一绕组端为同名端，所以它满足振荡的相位条件，即以该交流等效电路为基础构成的振荡电路可以产生振荡。

　　在图3.1（b）电路中，发射极相接的绕组端与集电极相接的另一绕组端为同名端（注意，都不打点也属于同名端），所以它满足振荡的相位条件，即以该交流等效电路为基础构成的振荡电路可以产生振荡。

　　在图3.1（c）电路中，发射极相接的绕组端与基极相接的另一绕组端为异名端，所以它不满足振荡的相位条件，即以该交流等效电路为基础构成的振荡电路不能产生振荡。

　　在图3.1（d）电路中，对于有抽头的绕组，由于绕组有一端接地，因而电极与抽头相接处的同名端，可移至另一不接地的绕组端处，所以发射极相接的绕组端与基极相接的另一绕组端为同名端，因此它满足振荡的相位条件，即以该交流等效电路为基础构成的振荡电路可以产生振荡。

　　

　　3.2 、三点式振荡器

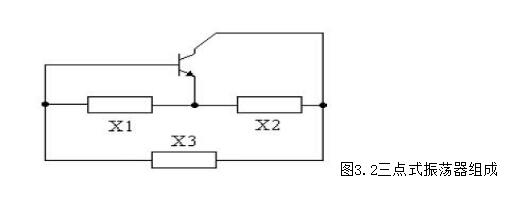
　　三点式振荡电路是指作为选频网络的LC谐振回路（兼做反馈网络）的三个

　　端点分别与晶体管的三个电极相连接的LC正弦波振荡电路。其交流通路的一般结构如图3.2所示，图中X1、X2、X3表示组成LC谐振回路各元件的电抗，输出电压通过X1反馈到放大电路的输入端。这类振荡器在判断相位条件时可采用在瞬时极性法基础上总结出的更为简单的方法，即只要电路中三个电抗元件满足下面两个条件，电路就可振荡：X1①与X2应为同性电抗元件（都为容性或都为感性），X3②应与X1、X2互为异性电抗元件（感性与容性互为异性）。为了便于记忆，可以概括为“射同基反”的构成规则。