

视觉定位原理:对极几何与基本矩阵
编程实验
描述
本文为大家介绍对极几何与基本矩阵这两个视觉定位原理。
对极几何
提到对极几何,一定是对二幅图像而言,对极几何实际上是“两幅图像之间的对极几何”,它是图像平面与以基线为轴的平面束的交的几何(这里的基线是指连接摄像机中心的直线),以下图为例:对极几何描述的是左右两幅图像(点x和x’对应的图像)与以CC’为轴的平面束的交的几何!
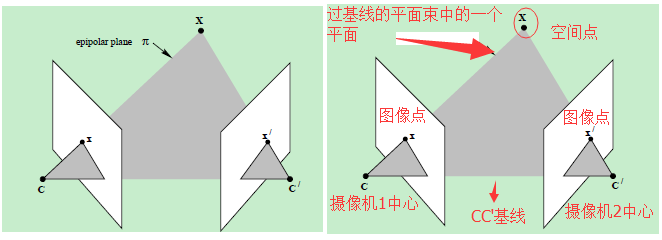
直线CC’为基线,以该基线为轴存在一个平面束,该平面束与两幅图像平面相交,下图给出了该平面束的直观形象,可以看到,该平面束中不同平面与两幅图像相交于不同直线;
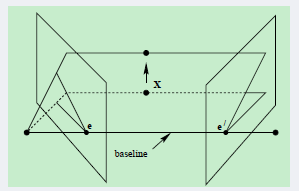
上图中的灰色平面π,只是过基线的平面束中的一个平面(当然,该平面才是平面束中最重要的、也是我们要研究的平面);
epipolarpoints极点
每一个相机的透镜中心是不同的,会投射到另一个相机像面的不同点上。这两个像点用eL和eR表示,被称为epipolarpoints极点。两个极点eL、eR分别与透镜中心OL、OR在空间中位于一条直线上。
epipolarplane极面
将X、OL和OR三点形成的面称为epipolarplane极面。
epipolarline极线
直线OL-X被左相机看做一个点,因为它和透镜中心位于一条线上。然而,从右相机看直线OL-X,则是像面上的一条线直线eR-XR,被称为epipolarline极线。从另一个角度看,极面X-OL-OR与相机像面相交形成极线。
极线是3D空间中点X的位置函数,随X变化,两幅图像会生成一组极线。直线OL-X通过透镜中心OL,右像面中对应的极线必然通过极点eR。一幅图像中的所有极线包含了该图像的所有极点。实际上,任意一条包含极点的线都是由空间中某一点X推导出的一条极线。
如果两个相机位置已知,则:
1.如果投影点XL已知,则极线eR-XR已知,点X必定投影到右像面极线上的XR处。这就意味着,在一个图像中观察到的每个点,在已知的极线上观察到该点的其他图像。这就是Epipolarconstraint极线约束:X在右像面上的投影XR必然被约束在eR-XR极线上。对于OL-XL上的X,X1,X2,X3都受该约束。极线约束可以用于测试两点是否对应同一3D点。极线约束也可以用两相机间的基本矩阵来描述。
2.如果XL和XR已知,他们的投影线已知。如果两幅图像上的点对应同一点X,则投影线必然交于X。这就意味着X可以用两个像点的坐标计算得到。
基础矩阵
如果已知基础矩阵F,以及一个3D点在一个像面上的像素坐标p,则可以求得在另一个像面上的像素坐标p‘。这个是基础矩阵的作用,可以表征两个相机的相对位置及相机内参数。
下面具体介绍基础矩阵与像素坐标p和p’的关系。
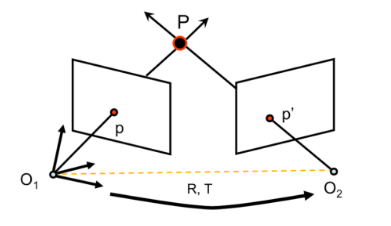
以O1为原点,光轴方向为z轴,另外两个方向为x,y轴可以得到一个坐标系,在这个坐标系下,可以对P,p1(即图中所标p),p2(即图中所标p‘)得到三维坐标,同理,对O2也可以得到一个三维坐标,这两个坐标之间的转换矩阵为[RT],即通过旋转R和平移T可以将O1坐标系下的点P1(x1,y1,z1),转换成O2坐标系下的P2(x2,y2,z2)。
则可知,P2=R(P1-T)(1)
采用简单的立体几何知识,可以知道
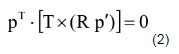
其中,p,p‘分别为P点的像点在两个坐标系下分别得到的坐标(非二维像素坐标)。Rp’为极面上一矢量,T为极面上一矢量,则两矢量一叉乘为极面的法向量,这个法向量与极面上一矢量p一定是垂直的,所以上式一定成立。(这里采用转置是因为p会表示为列向量的形式,此处需要为行向量)
采用一个常用的叉乘转矩阵的方法,
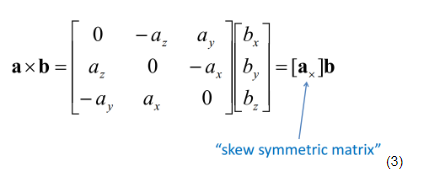
将我们的叉乘采用上面的转换,会变成
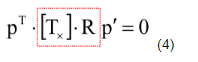
红框中所标即为本征矩阵E,他描述了三维像点p和p‘之间的关系
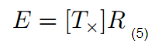
有了本征矩阵,我们的基础矩阵也就容易推导了
注意到将p和p‘换成P1和P2式(4)也是成立的,且有
q1=K1P1(6)
q2=K2P2(7)
上式中,K1K2为相机的校准矩阵,描述相机的内参数q1q2为相机的像素坐标代入式(4)中,得
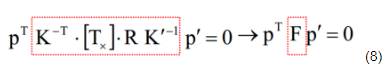
上式中p->q1,p‘->q2
这样我们就得到了两个相机上的像素坐标和基础矩阵F之间的关系了
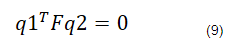
- 相关推荐
- 热点推荐
- 视觉定位
-
光纤矩阵,提升视觉体验新高度2023-09-01 1182
-
什么是向量?向量的点乘与几何意义是什么?2021-06-18 1282
-
融合3D场景几何信息的视觉定位算法2020-11-13 5748
-
【LabVIEW懒人系列教程-视觉入门】2.11LabVIEW视觉助手之几何测量2020-08-16 2351
-
医疗器械视觉定位应用2020-05-22 2810
-
自动驾驶的视觉定位与导航应用详细解析2020-04-28 1590
-
使用机器视觉进行刀具几何参数测量技术的资料说明2019-10-21 1402
-
labview 视觉 多模板匹配 教程2019-09-24 21787
-
视觉定位,旋转平移的问题:2019-09-01 3838
-
机器人视觉系统组成及定位算法分析2019-06-08 3648
-
LabVIEW 的Tripod 机器人视觉处理和定位研究2019-06-01 2829
-
【Labview日积月累】第一期 机器视觉讲解2016-05-09 68507
-
应用AutoCAD几何计算器实现快速定位2009-02-14 1692
-
GPS定位的几何关系图2008-08-06 1515
全部0条评论

快来发表一下你的评论吧 !

