

rc并联电路充放电时间计算方法
应用电子电路
描述
RC 并联电路既可通过直流又可通过交流信号。它和 RC 串联电路有着同样的转折频率:f0=1/2πR1C1。当输入信号频率小于f0时,信号相对电路为直流,电路的总阻抗等于 R1;当输入信号频率大于f0 时C1 的容抗相对很小,总阻抗为电阻阻值并上电容容抗。当频率高到一定程度后总阻抗为0。
电容充放电
当电容器接通电源以后,在电场力的作用下,与电源正极相接电容器极板的自由电子将经过电源移到与电源负极相接的极板下, 正极由于失去负电荷而带正电, 负极由于获得负电荷而带负电,正,负极板所带电荷大小相等,符号相反。电荷定向移动形成电流,由于同性电荷的排斥作用,所以开始电流最大,以后逐渐减小,在电荷移动过程中,电容器极板储存的电荷不断增加,电容器两极板间电压 Uc 等于电源电 压U时电荷停止移动,电流 I=0,开关闭合,通过导线的连接作用,电容器正负极板电荷中和掉。 当K闭合时,电容器C正极正电荷可以移动 负极上中和掉,负极负电荷也可以移到正极中和掉,电荷逐渐减少,表现电流减小,电压也逐渐减小为零。
①、充电
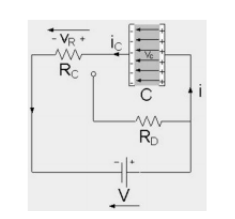
图1 电容充电
见图1,电路中有电流流通。两块板会分别获得数量相等的相反电荷,此时电容正在充电,其两端的电位差vc逐渐增大。一旦电容两端电压vc增大至与电源电压V相等时,vc = V,电容充电完毕,电路中再没有电流流动,而电容的充电过程完成。
由于电容充电过程完成后,就没有电流流过电容器,所以在直流电路中,电容可等效为开路或R = ∞,电容上的电压vc不能突变。
②、放电
当切断电容和电源的连接后,电容通过电阻RD进行放电,两块板之间的电压将会逐渐下降为零,vc = 0,见图2。
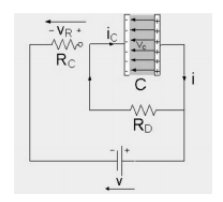
图2 电容放电
③、时间常数
两图中,RC和RD的电阻值分别影响电容的充电和放电速度。 电阻值R和电容值C的乘积被称为时间常数τ,这个常数描述电容的充电和放电速度,见图3。
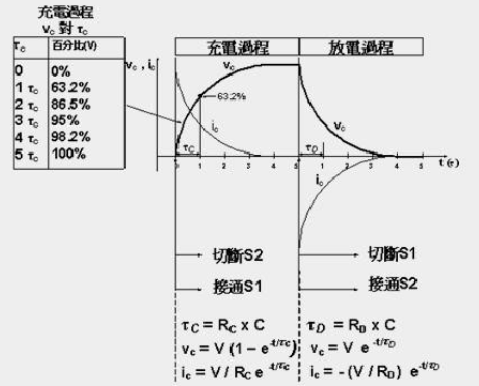
图3 电容充放电时间常数图
电容值或电阻值愈小,时间常数也愈小,电容的充电和放电速度就愈快,反之亦然。 电容几乎存在于所有电子电路中,它可以作为“快速电池”使用。如在照相机的闪光灯中,电容作为储能元件,在闪光的瞬间快速释放能量。
其中,充放电过程中的电压和电流计算公式如图4。
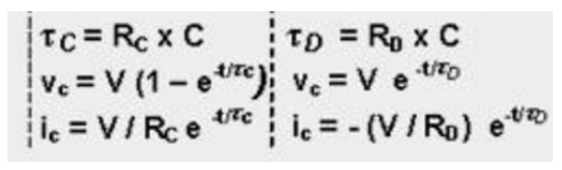
图4 电容充放电中的电压VC和电流iC
rc并联电路充放电时间计算
V0 为电容上的初始电压值;
V1 为电容最终可充到或放到的电压值; Vt 为t时刻电容上的电压值。 则,
Vt=“V0”+(V1-V0)* [1-exp(-t/RC)] 或,
t = RC*Ln[(V1-V0)/(V1-Vt)]
求充电到90%VCC的时间。(V0=0,V1=VCC,Vt=0.9VCC) 代入上式: 0.9VCC=0+VCC*[[1-exp(-t/RC)] 既 [[1-exp(-t/RC)]=0.9; exp(-t/RC)=0.1 - t/RC=ln(0.1)
t/RC=ln(10) ln10约等于2.3 也就是t=2.3RC。 带入R=10k C=10uf得。 t=2.3*10k*10uf=230ms
RC回路充放电时间的推导过程需要用高等数学,简单的方法只要记住RC回路的时间常数τ=R×C,在充电时,每过一个τ的时间,电容器上电压就上升(1-1/e)约等于0.632倍的电源电压与电容器电压之差;放电时相反。
如C=10μF,R=10k,则τ=10e-6×10e3=0.1s 在初始状态Uc=0时,接通电源,则过0.1s(1τ)时,电容器上电压Uc为0+(1-0)×0.632=0.632倍电源电压U,到0.2s(2τ)时,Uc为0.632+(1-0.632)×0.632=0.865倍U……以此类推,直到t=∞时,Uc=U。放电时同样运用,只是初始状态不同,初始状态Uc=U。
-
电容充放电时间计算2012-08-13 0
-
RC电容充放电时间计算公式2018-05-16 0
-
RC充放电路的原理是什么呢2022-03-02 0
-
电容充放电时间的计算12016-05-06 1132
-
超级电容容量及放电时间的计算方法2017-03-01 1534
-
电阻串联和并联的计算方法_电阻串联和并联的作用2018-01-21 213862
-
探讨电容充放电时间的计算方法2018-09-10 66998
-
SAR ADC外部RC滤波电路的理论计算方法2019-04-12 6844
-
电容充放电时间的计算方法2019-05-29 141724
-
rc充放电时间计算公式2023-11-20 776
-
为什么时间常数的大小决定了RC电路充放电的快慢?2023-11-20 4351
-
RC时间常数的概念、计算方法和在实际应用中的重要性2023-11-20 15589
-
RC电路是什么?为什么充放电慢?2023-11-20 2349
-
RC串联电路的特点是什么?RC电路如何计算延时时间呢?2023-11-20 5791
-
RC充放电电路原理解析及LTspice仿真2023-11-22 10560
全部0条评论

快来发表一下你的评论吧 !

