如何通过霍尔效应测量半导体中电子和空穴的迁移率?

在半导体中，除了能带宽度外，一个重要的物理量是电荷载流子(电子和空穴)的迁移率。在本教程中，我们将研究霍尔效应，这使我们能够实验性地确定半导体中的这一物理量。

 

电荷载流子迁移率

 

在本篇文章中，我们将采用在早期期刊中探讨的德鲁德-洛伦兹框架。我们回顾一下，这一模型完全基于经典力学。唯一的“外部”成分是电子的有效质量m∗;这是一种数学手段，使我们能够将电子视为不受力的经典粒子。通过这种方式，我们避免了量子复杂性，因为我们需要考虑晶格离子施加的周期性势能。极端总结如下场景：一个电子与一个离子发生非弹性碰撞，失去其所有的动能。

 

施加一个均匀的静电场 E 会加速电子;加速度向量的大小为 a=m∗eE​，其中 e 是电子电荷的绝对值。如果 τr​ 是一次碰撞与下次碰撞之间的平均时间(弛豫时间)，则电子在经历新碰撞的瞬间速度向量的大小为 vd​=aτr​，其中我们识别出在前一篇文章中我们通过软件重构的漂移速度。转向相应的向量量(请记住在我们的符号中，电子电荷为 e<0，我们得到：

其中 n 是电子的数密度。电流密度向量 j 的方向与电场相同，而漂移速度则朝相反方向。从方程(1)中的欧姆定律可以推导出：

其中 σ 是电导率。

在室温下，上述描述的场景再现了金属的电气行为。这些结果很容易扩展到半导体，只要在 σ 的表达式中包含空穴的贡献，其中空穴有一个有效质量 ℎ∗mh∗​，通常与电子质量不同。假设两种电荷载流子的时间 τr​ 相同是一种良好的近似(更复杂的模型则假设 τr​ 不仅依赖于载流子的符号，还依赖于单个电子/空穴)。

电导率的解析表达式通过定义电子和空穴的迁移率可以得到一个更易于处理的形式：

方程(3)从微观角度定义了迁移率。考虑到上述公式，我们得出一种宏观定义，即电荷载流子的迁移率是其漂移速度与电场的比值。从实验的角度来看，量(3)可以通过霍尔效应来确定。在进入这个十九世纪发现的过程之前，我们必须澄清一些电磁学的概念。

 

磁场：B还是H

 

在关于电磁学的旧出版物中，假定 H(磁场强度)是基本向量，而 B(磁感应)是派生向量。然而，为了保持电量和磁量之间的对称性，有必要将 B 视为基本向量。令人困惑的是，在静电学中，电场强度 E 被视为基本向量，而电位移 D 是派生向量。

 

但在观察麦克斯韦方程时，为了建立电荷与电流之间的对称性，以及差分算子散度和旋度之间的对称性，我们必须将 B 视为基本向量。在许多固态物理文献中，H 出现在方程中，并说明该量与 B 相同，因为未考虑铁磁材料。为了避免误解，在我们的方程中，B 将作为磁场出现。

 

另一个问题是：“使用哪种单位制，国际单位制 (SI) 还是高斯单位制?”答案取决于读者。如果他是物理学家，他会回答：“高斯”。如果他是工程师，他会回答：“国际单位制”。高斯单位制更适合亚原子过程，而 SI(或合理化的 MKS)则适用于宏观系统。我们将使用 SI，其中 B 以 Wb/m2Wb/m2 为单位。

霍尔效应

 

在霍尔效应中，关键角色由洛伦兹力 F 负责，即作用于以速度 v 在磁场 B 中移动的电荷 q 的力。在国际单位制中：

 

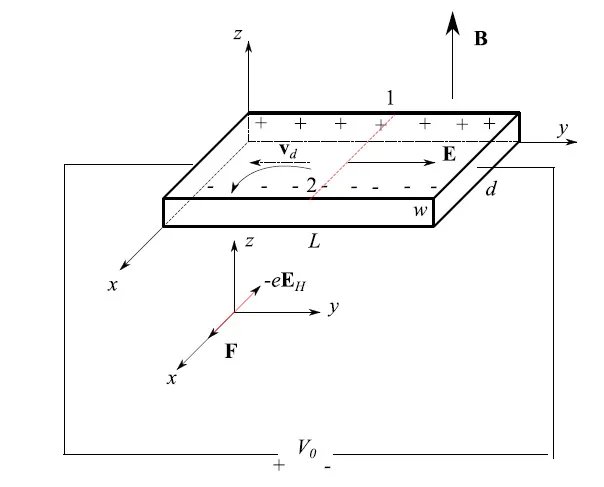
我们考虑图 1 中所示的实验配置，在这个配置中，我们对一个具有平行六面体形状的金属导体的两端施加一个恒定的电压差 0V0​，其边长为 L,d,w。在均匀和各向同性的条件下，将建立一个沿 y 轴方向的均匀静电场：E=(0,E,0)。这导致电流密度 j 与电场向量 E 平行且一致，而速度向量则朝相反方向(如图 1 中的虚线所示)。构成导体的材料的均匀性和各向同性，加上热平衡，保证了如上所述的直线轨迹。

 

激活一个均匀的磁静场 B=(0,0,B) 产生一个洛伦兹力 F，其方向如图 1 所示，偏转单个电子的轨迹。由于导体的任何横截面都是一个开路，因此电子无法无限流动。最终结果是在一个边缘上出现负电荷的过剩(图 1);随后将建立一个名为霍尔场 EH​ 的电场。更确切地说，当霍尔场施加的力与洛伦兹力 F 相等且方向相反时，将达到平衡，如图 1 中的力图所示。通过速度向量与磁场正交，可以轻松展开表示洛伦兹力的向量积。

 

应用动态平衡条件，我们可以轻松得到：EH​=vd​B，现在如果我们随意选取导体的一个横截面 ΣΣ，在点 1 和点 2 之间(图 1)，将建立一个电压差 VH​=EH​d(霍尔电压)。考虑到 EH​ 的表达式，并将 vd​ 表示为电流密度 j 的函数，因此电流强度为 i=jS，其中 S=wd 是 ΣΣ 的面积，我们得到：

其中 RH​=ne1​ 是霍尔系数，即电荷密度的倒数。考虑到(3)中的第一个公式，我们最终得到：

在方程(5)中，B 和 w 已知。量 VH​ 和 i 可以被测量，因此我们可以计算 RH​;假设已知电导率 σ，(6)使我们能够确定 μe​。不幸的是，对于金属来说，由于电子数密度很高，VH​ 太低;实际上，霍尔电压与 RH​ 成正比，即与电荷密度的倒数成正比。这在半导体中并不发生(此时电荷密度降低了大约 105105 倍)，注意到所获得的结果很容易通过引入空穴的迁移率来扩展。我们邀请读者为一块 p 型硅条确定空穴的迁移率，其条件为：

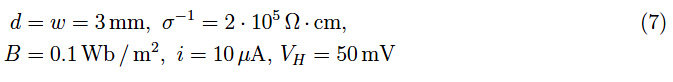
结论

所提出的实验使我们能够在室温下确定迁移率。考虑极端温度的模型更加复杂，例如在航天探测器上的半导体器件中发生的温度。相反的极限(高温)也是电力电子的一个典型问题。