

基于场景的自动驾驶验证策略
描述
基于场景的自动驾驶验证策略
引言
自动驾驶功能的出现可以很大地降低由人为因素造成的交通事故,随之如何检验和验证自动驾驶系统及车辆的可靠性变得至关重要。但常见的测试验证手段通常伴随着高昂的投入成本,因此使得验证过程变得十分困难。一个可选方案是将实际交通状况做出总结生成具有高度代表性的交通场景,通过仿真分析自动驾驶系统在这些场景上的安全性。然而交通场景中元素的复杂性与失败事件的罕见性导致难于准确分析系统失败的概率和造成系统失败的原因。本文将针对此难题,介绍一种将场景降维并极大提高分析系统失败概率准确性的方法。
二模型定义
1.基本流程
基于 ISO 21448预期功能安全分析方法论,确定自动驾驶算法的ODD/ODC,对自动驾驶算法进行危害事件分析,将已知危害场景作为抓手,对其进行充分泛化仿真,并且挖掘未知危害场景,将未知危害场景变为已知危害场景。

本文将场景按照抽象程度分为功能场景、逻辑场景和具体场景。将真实世界中驾驶场景和ODD/ODC描述为逻辑场景的集合,通过分析每个逻辑场景的发生频率与自动驾驶系统在其中的失败概率估计自动驾驶系统在真实世界中的失败概率。
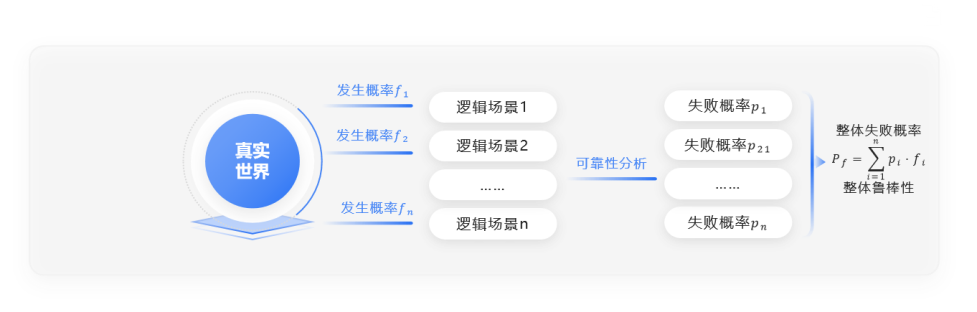
2.失败概率估算方法
为了更好地分析自动驾驶系统的失败概率,用概率空间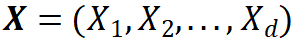 来表示一个逻辑场景,其中
来表示一个逻辑场景,其中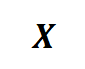 伴随概率密度函数
伴随概率密度函数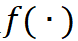 。而此逻辑场景下的一个具体场景可以表示为此空间中的一个点
。而此逻辑场景下的一个具体场景可以表示为此空间中的一个点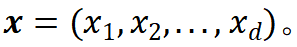
用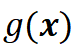 表示自动驾驶系统在具体场景
表示自动驾驶系统在具体场景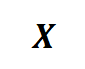 中的某项评价指标,并不失一般性地定义该系统失败定义为
中的某项评价指标,并不失一般性地定义该系统失败定义为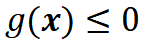 。故该系统在一个逻辑场景中的失败概率可以表达为
。故该系统在一个逻辑场景中的失败概率可以表达为
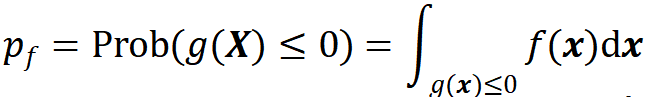
若第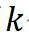 个逻辑场景在
个逻辑场景在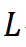 公里的平均出现频率为
公里的平均出现频率为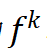 ,则根据贝叶斯定理此被测试车辆或算法
,则根据贝叶斯定理此被测试车辆或算法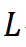 在公里上的平均失败率为
在公里上的平均失败率为
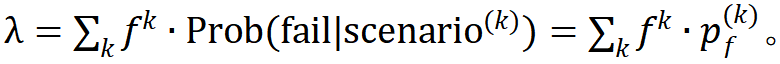
3.难题
由于自动驾驶算法本身的未知性,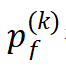 往往无法直接计算,而空间的复杂性与失败的罕见性引起的维度灾难和罕见性灾难又导致无法通过蒙特卡罗方法简单估计
往往无法直接计算,而空间的复杂性与失败的罕见性引起的维度灾难和罕见性灾难又导致无法通过蒙特卡罗方法简单估计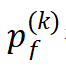 。故如何构建统计量来高效估计各个场景中的失败概率成为核心问题。
。故如何构建统计量来高效估计各个场景中的失败概率成为核心问题。
三敏感性分析
1.敏感性分析的目标
大量经验表明系统表现并非依赖于场景中的全部元素,往往场景中部分元素取值即可以确定系统的表现是否会导致系统失效或出错。这为基于场景的自动驾驶系统验证提供了一种降维策略,即通过敏感性分析从众多参数中挑选真正对自动驾驶系统表现产生影响的关键参数。敏感性分析过程在概率空间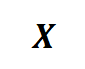 中采集具有代表性的样本
中采集具有代表性的样本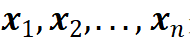 并通过并行仿真获取自动驾驶系统在这些样本上的表现
并通过并行仿真获取自动驾驶系统在这些样本上的表现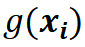 。通过对这些数据进行统计分析,计算各个参数对车辆表现的重要性,即各个参数对
。通过对这些数据进行统计分析,计算各个参数对车辆表现的重要性,即各个参数对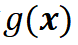 的敏感性。
的敏感性。
2.样本策略
样本采集策略大体分为固定策略和随机/拟随机策略。其中固定样本策略又可以分为全因子法和部分因子法;随机样本策略分为单纯蒙特卡罗方法以及按照不同目标优化的拉丁超立方采样;拟随机策略主要指各种低差异性序列采样。固定样本策略可以在维度相对较低时有效分析自变量和因变量间的线性或二次线性关系,而当维度上面或因果关系复杂时此方法会导致计算困难。随机/拟随机样本策略则可以适应更复杂的因果关系和更高的空间维度。例如下图分别使用拉丁超立方采样(右图)和三水平下的全因子法(左图)分析函数
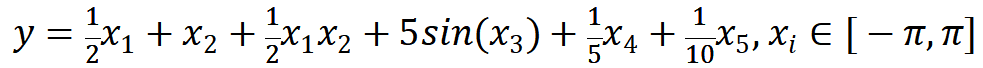
中的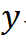 与
与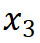 因果关系。
因果关系。
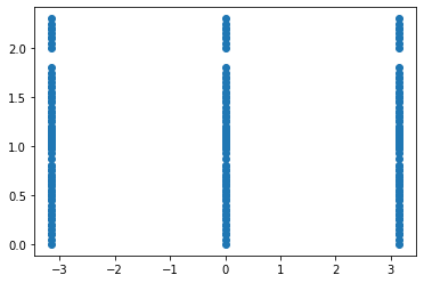
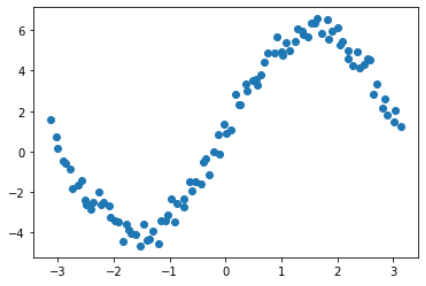
可以明显看出随机/拟随机策略使用的拉丁超立方采样可以更好的体现因变量关于自变量的变化,同时在5因子3水平采样中,全因子法需要的样本数为3^5=243也远大于拉丁超立方采样用的100个。
3.分析指标
自变量对因变量重要性可以通过因变量关于自变量的变化率即偏导数、因变量和自变量间的不同相关性系数(皮尔斯、斯皮尔曼、坎德尔等)、因变量概率密度函数关于自变量变化的敏感程度即基于条件概率的敏感性、因变量方差关于自变量变化的敏感程度即基于方差的敏感性、模拟拟合的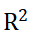 及模型拟合的预测能力等几个方面评价。其中偏导数不适应全局敏感性分析,各种相关性系数仅能适应单调变化,模拟拟合的
及模型拟合的预测能力等几个方面评价。其中偏导数不适应全局敏感性分析,各种相关性系数仅能适应单调变化,模拟拟合的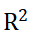 只能反应训练集容易过拟合。故我们推荐使用基于条件概率/条件方差的敏感性指标+模型拟合预测能力指标COP结合的策略,先确定各个参数重要性的顺序再根据COP最终选取对结果有影响的参数组合。
只能反应训练集容易过拟合。故我们推荐使用基于条件概率/条件方差的敏感性指标+模型拟合预测能力指标COP结合的策略,先确定各个参数重要性的顺序再根据COP最终选取对结果有影响的参数组合。
四失败概率估计
成熟的自动驾驶系统对安全的要求十分严格,需要精准估计系统的失败概率。而造成完善系统失败的场景属于罕见事件,使用蒙特卡罗方法难以寻找并精准估计其发生概率。我们推荐使用方向采样和重要性采样算法来来寻找失败场景并估计失败概率。
五数值实验
我们使用一个显示函数来举例说明。选取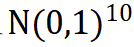 空间中Katsuki函数作为KPI函数,即
空间中Katsuki函数作为KPI函数,即
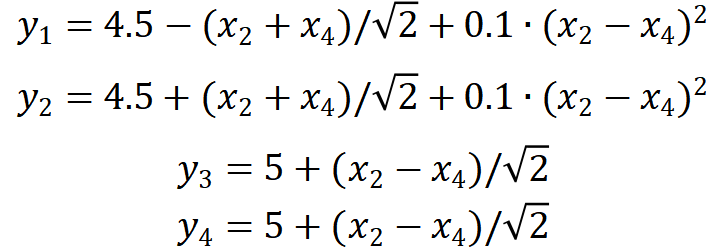 KPI
KPI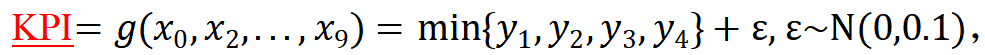
并以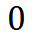 作为失败阈值,下面将通过敏感性分析和可靠性分析寻找影响系统表现的变量并估计系统失败概率
作为失败阈值,下面将通过敏感性分析和可靠性分析寻找影响系统表现的变量并估计系统失败概率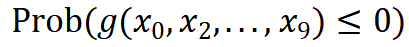 。
。
首先使用拉丁超立方采样在空间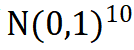 进行采样,样本量为200,并使用基于条件概率和条件方差的敏感性指标对计算结果展示如下:
进行采样,样本量为200,并使用基于条件概率和条件方差的敏感性指标对计算结果展示如下:
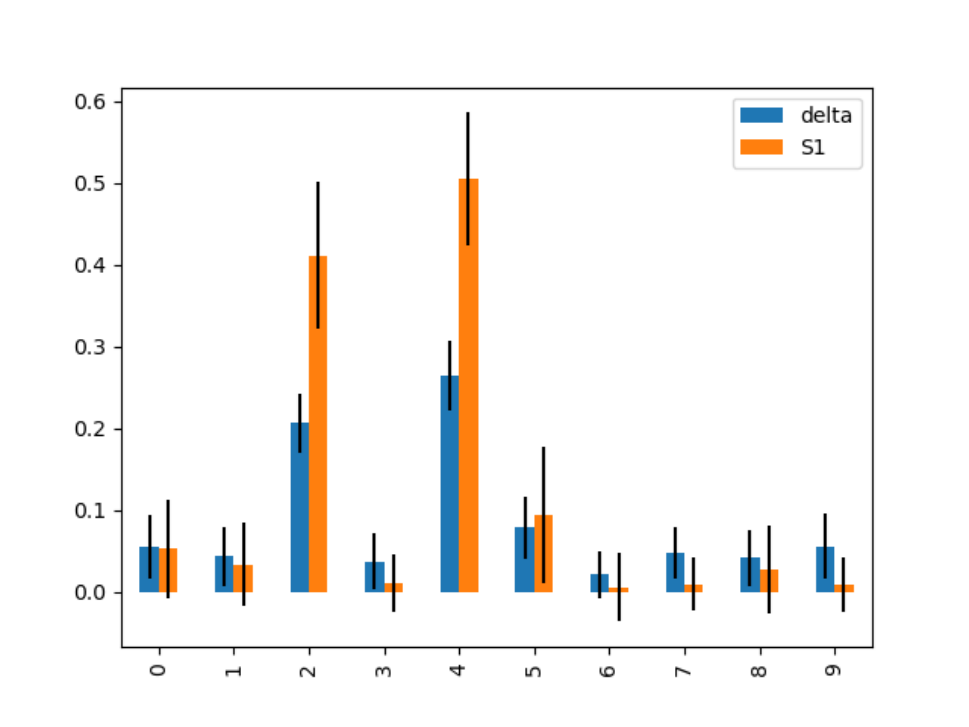
横轴为对应的变量顺序,纵轴为指标数值,橙色为基于条件方差的敏感性指标,蓝色为基于条件概率的敏感性指标,黑色的竖线为指标对应的致信区间
通过上面的数据分析图可以清楚看出因变量对于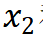 和
和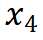 的变化非常敏感,对剩余的变量不敏感。拟合因变量关于自变量的回归模型并基于交叉验证计算可以得到
的变化非常敏感,对剩余的变量不敏感。拟合因变量关于自变量的回归模型并基于交叉验证计算可以得到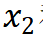 和
和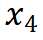 组合的最优COP=98.81%,即因变量COP=98.81%的不确定性可以由
组合的最优COP=98.81%,即因变量COP=98.81%的不确定性可以由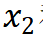 和
和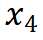 的变化解释,故将原始
的变化解释,故将原始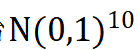 的空间降维成由
的空间降维成由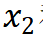 和
和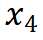 组成的
组成的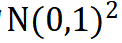 空间。
空间。
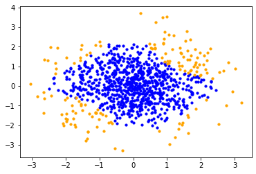
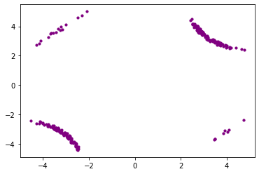
接下来使用重要性采样在降维后的参数空间中分析系统的失败概率。其中参数配置为每次迭代计算1000个实验点,并保留其中最优的15%估计轮迭代的提议函数。具体结果展示如下:

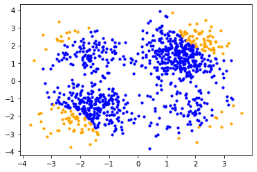
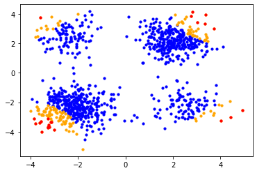
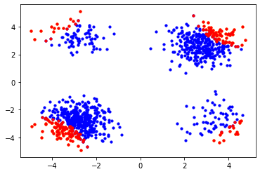
上面的表格说明可靠性分析算法在降维后的空间中高效寻找到的失败场景并估计其失败概率。下面的图片展示每轮采样中样本分布及KPI变化,其中蓝色的点表示安全场景,黄色的点表示较为危险的场景,红色点表示失败场景,最后紫色的点表示寻找到的失败临界。
六应用案例
1.场景设置
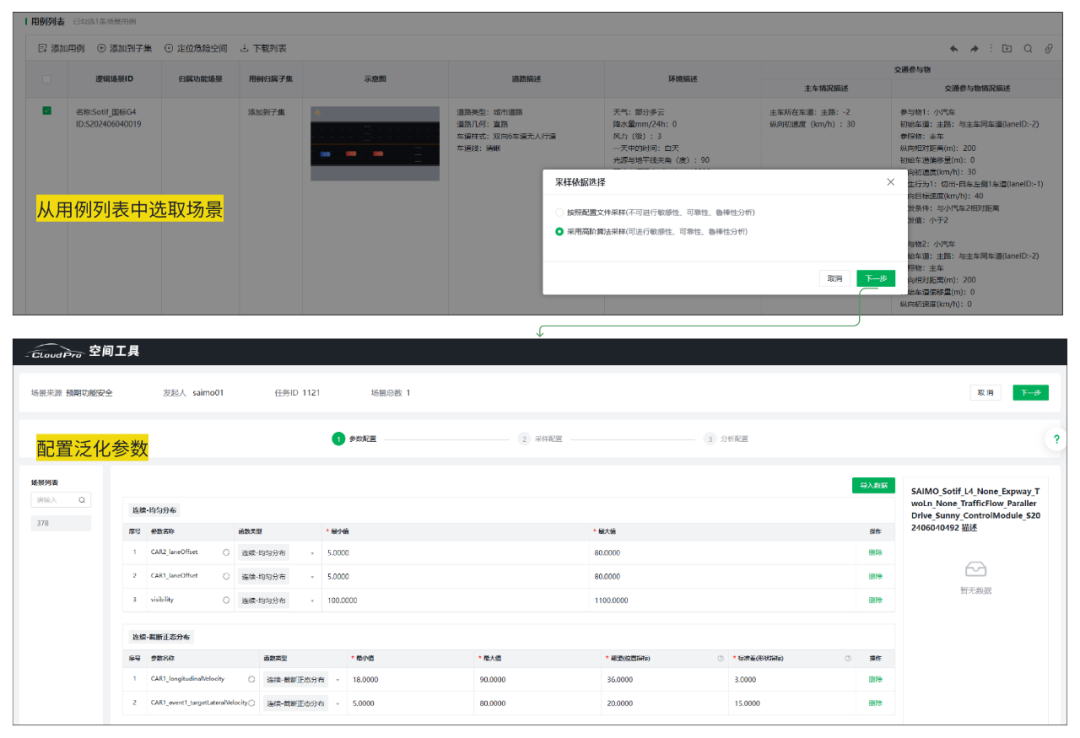
基于国标G.4场景改造的逻辑场景,即双车道、存在2辆环境车.初始环境下按照Ego、VT1、VT2从后到前的顺序同属左车道,VT2属于静止状态,Ego与VT1向前行驶。
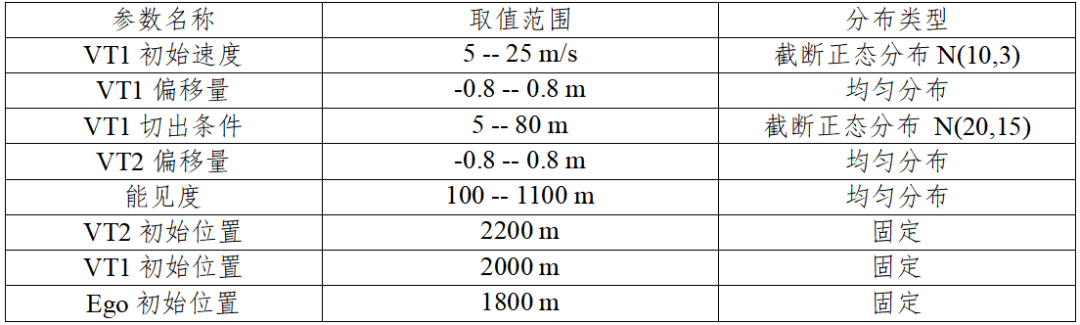
固定Ego、VT1、VT2的初始位置,相对距离为200米,对能见度、VT1初始速度、VT1与VT2的偏移、VT1触发切出时与VT2的距离进行泛化,并以TTC作为考核指标。AD算法使用第三方提供的自动驾驶算法对车辆横纵向行为进行控制。参数的泛化如下表所示
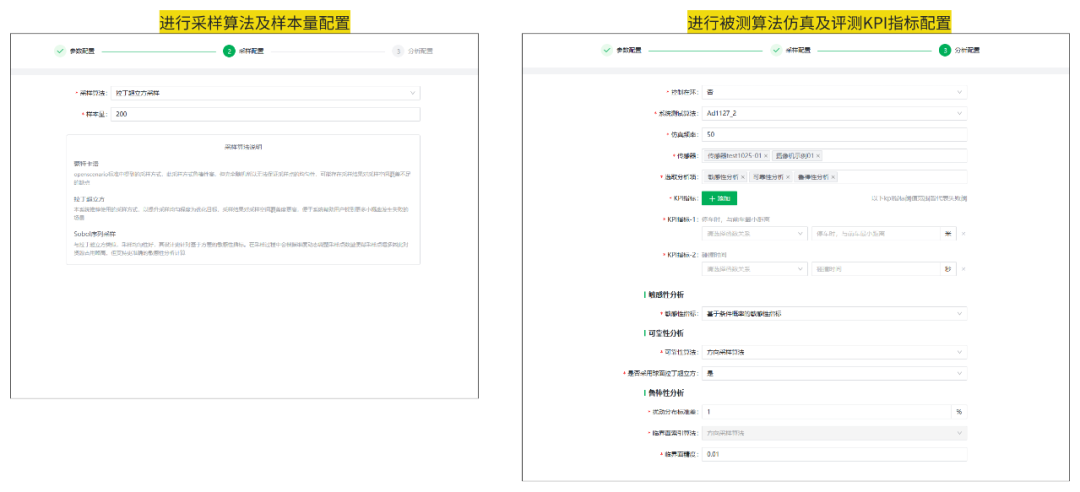
在进行采样算法样本量及被测算法仿真及评测设置后开展敏感性、可靠性分析。
2.敏感性分析
分别使用基于方差和基于概率的敏感性指标做出分析,结果均表明能见度、车道偏移量对TTC变化不明显,而VT1初始速度及切出时间对TTC的变化起显著作用。故后续分析将不再泛化能见度及车道偏移量3个参数,仅专注于对TTC有影响的变量实现空间降维。
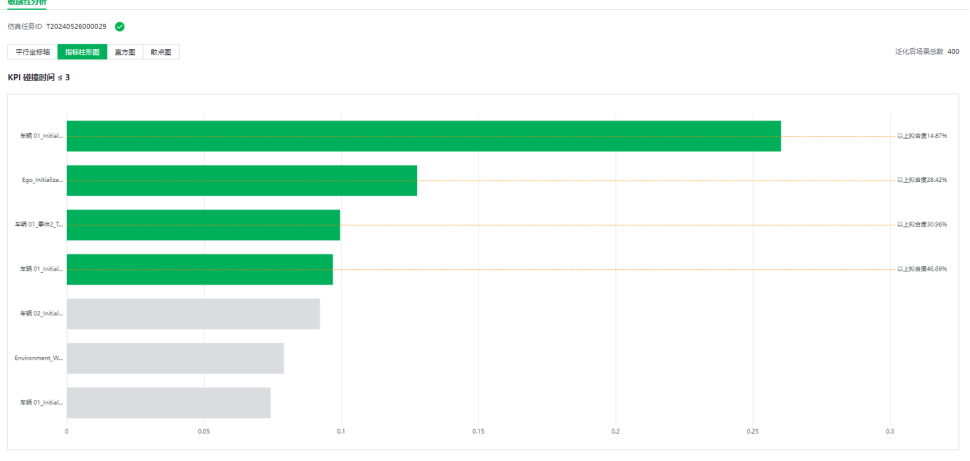
3.可靠性分析
用自适应重要性采样对该AD在该逻辑场景中的失败概率做出分析。其中每轮采样数量为400,保留最优样本比例为3%(保证最后用来估计失败概率的失败样本数量>=3%*400=12)。分别以TTC<3和TTC<2作为失败阈值,使用可靠性分析算法可以得到如下失败概率:

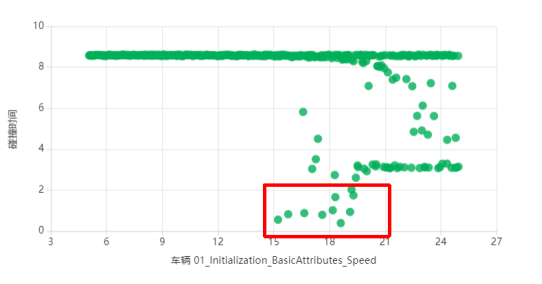
对AD算法的表现做出分析,可以看出危险场景并非处于边角处,故定步长泛化可能无法探索到失败场景。
若使用单纯蒙特卡罗法找到足够失败场景(20个)来估计失败率,则分别需要超过55000次和520000仿真。可靠性分析算法相较蒙特卡罗法分别节约97%和99.5%以上的成本。
通过上述方法,赛目推出Safety Pro结合云平台的并行仿真、加速计算能力,实现预期功能安全分析、参数敏感性分析、失败概率计算以及寻找失败临界面等功能,基于结果数据评估系统残余风险,若存在不可接受风险,则形成优化迭代策略,并且通过验证手段提前判断优化策略是否起效,助力、加速自动驾驶系统的开发和验证。

-
FPGA在自动驾驶领域有哪些应用?2024-07-29 8174
-
自动驾驶测试场景技术发展与应用2023-06-06 854
-
自动驾驶技术的实现2021-09-03 3074
-
自动驾驶系统设计及应用的相关资料分享2021-08-30 2301
-
网联化自动驾驶的含义及发展方向2021-01-12 4822
-
自动驾驶车的人车交互接口设计方案2020-07-30 2868
-
转发:聊聊边缘计算在自动驾驶中的应用场景2020-07-21 4820
-
自动驾驶汽车的处理能力怎么样?2019-08-07 2792
-
如何让自动驾驶更加安全?2019-05-13 3622
-
UWB主动定位系统在自动驾驶中的应用实践2018-12-14 3186
-
自动驾驶的到来2017-06-08 7305
-
自动驾驶真的会来吗?2016-07-21 14085
-
【话题】特斯拉首起自动驾驶致命车祸,自动驾驶的冬天来了?2016-07-05 13713
-
谷歌的自动驾驶汽车是酱紫实现的吗?2011-06-14 4668
全部0条评论

快来发表一下你的评论吧 !

