巴特沃斯滤波器c语言代码

巴特沃斯滤波器是电子滤波器的一种。巴特沃斯滤波器的特点是通频带的频率响应曲线最平滑。这种滤波器最先由英国工程师斯蒂芬·巴特沃斯（Stephen Butterworth）在1930年发表在英国<无线电工程>期刊的一篇论文中提出的。

巴特沃斯滤波器的次数

根据给定的参数设计模拟滤波器，然后进行变数变换，求取数字滤波器的方法，称为滤波器的间接设计。做为数字滤波器的设计基础的模拟滤波器，称之为原型滤波器。这里，我们首先介绍的是最简单最基础的原型滤波器，巴特沃斯低通滤波器。由于IIR滤波器不具有线性相位特性，因此不必考虑相位特性，直接考虑其振幅特性。

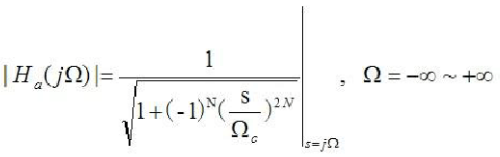
在这里，N是滤波器的次数，Ωc是截止频率。从上式的振幅特性可以看出，这个是单调递减的函数，其振幅特性是不存在纹波的。设计的时候，一般需要先计算跟所需要设计参数相符合的次数N。首先，就需要先由阻带频率，计算出阻带衰减

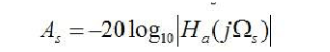
将巴特沃斯低通滤波器的振幅特性，直接带入上式，则有

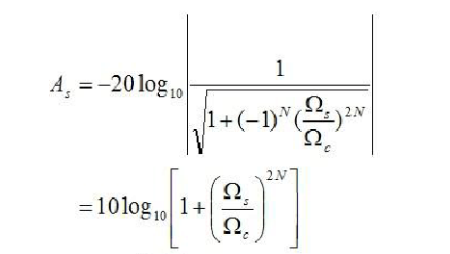
最后，可以解得次数N为

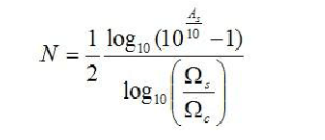
当然，这里的N只能为正数，因此，若结果为小数，则舍弃小数，向上取整。

巴特沃斯滤波器的传递函数

巴特沃斯低通滤波器的传递函数，可由其振幅特性的分母多项式求得。其分母多项式

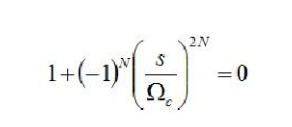
根据S解开，可以得到极点。这里，为了方便处理，我们分为两种情况去解这个方程。当N为偶数的时候，

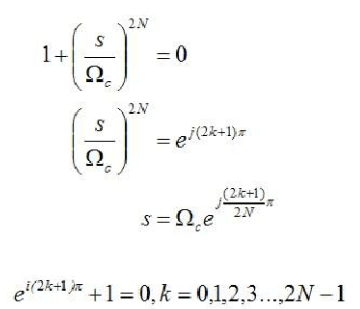
这里，使用了欧拉公式。同样的，当N为奇数的时候，

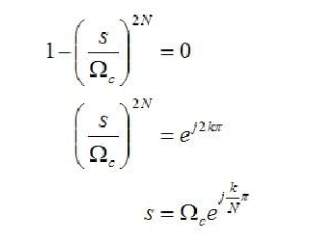
同样的，这里也使用了欧拉公式。归纳以上，极点的解为

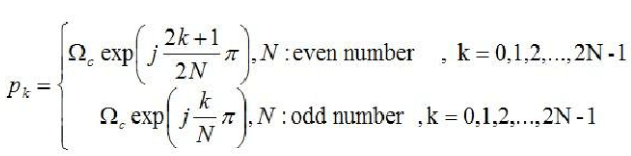
上式所求得的极点，是在s平面内，在半径为Ωc的圆上等间距的点，其数量为2N个。为了使得其IIR滤波器稳定，那么，只能选取极点在S平面左半平面的点。选定了稳定的极点之后，其模拟滤波器的传递函数就可由下式求得。

巴特沃斯滤波器的实现（C语言）

首先，是次数的计算。次数的计算，我们可以由下式求得。

其对应的C语言程序为

N = Ceil（0.5*（ log10 （ pow （10， Stopband_attenuation/10） - 1） /

log10 （Stopband/Cotoff） ））;

然后是极点的选择，这里由于涉及到复数的操作，我们就声明一个复数结构体就可以了。最重要的是，极点的计算含有自然指数函数，这点对于计算机来讲，不是太方便，所以，我们将其替换为三角函数，

这样的话，实部与虚部就还可以分开来计算。其代码实现为

typedef struct

{

double Real_part;

double Imag_Part;

} COMPLEX;

COMPLEX poles［N］;

for（k = 0;k <= （（2*N）-1） k++）

{

if（Cotoff*cos（（k+dk）*（pi/N）） < 0）

{

poles［count］.Real_part = -Cotoff*cos（（k+dk）*（pi/N））;

poles［count］.Imag_Part= -Cotoff*sin（（k+dk）*（pi/N））;

count++;

if （count == N） break;

}

}

计算出稳定的极点之后，就可以进行传递函数的计算了。传递的函数的计算，就像下式一样

这里，为了得到模拟滤波器的系数，需要将分母乘开。很显然，这里的极点不一定是整数，或者来说，这里的乘开需要做复数运算。其复数的乘法代码如下，

int Complex_Multiple（COMPLEX a，COMPLEX b，

double *Res_Real，double *Res_Imag）

{

*（Res_Real） = （a.Real_part）*（b.Real_part） - （a.Imag_Part）*（b.Imag_Pa

rt）;

*（Res_Imag）= （a.Imag_Part）*（b.Real_part） + （a.Real_part）*（b.Imag_Par

t）;

return （int）1;

}

有了乘法代码之后，我们现在简单的情况下，看看其如何计算其滤波器系数。我们做如下假设

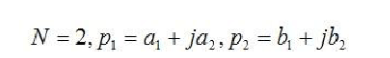
这个时候，其传递函数为

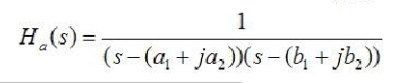
将其乘开，其大致的关系就像下图所示一样。

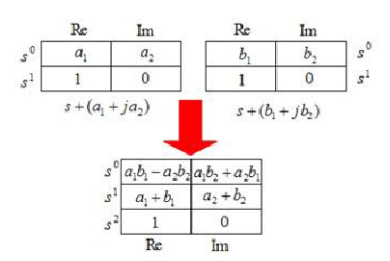
Res［0］.Real_part = poles［0］.Real_part;

Res［0］.Imag_Part= poles［0］.Imag_Part;

Res［1］.Real_part = 1;

Res［1］.Imag_Part= 0; 5.

for（count_1 = 0;count_1 < N-1;count_1++）

{

for（count = 0;count <= count_1 + 2;count++）

{

if（0 == count）

{

Complex_Multiple（Res［count］， poles［count_1+1］，

&（Res_Save［count］.Real_part），

&（Res_Save［count］.Imag_Part））;

}

else if（（count_1 + 2） == count）

{

Res_Save［count］.Real_part += Res［count - 1］.Real_part;

Res_Save［count］.Imag_Part += Res［count - 1］.Imag_Part;

}

else

{

Complex_Multiple（Res［count］， poles［count_1+1］，

&（Res_Save［count］.Real_part），

&（Res_Save［count］.Imag_Part））;

1 Res_Save［count］.Real_part += Res［count - 1］.Real_part;

Res_Save［count］.Imag_Part += Res［count - 1］.Imag_Part;

}

}

*（b+N） = *（a+N）;