

使用实时采样示波器测量相位噪声
测量仪表
描述
什么是相位噪声?
维基百科对相位噪声的定义是:“波形相位在频域中的快速、短期、随机波动,由时域的不稳定(抖动)引起。”噪声一词的定义说明该术语不涉及任何杂散项或确定项。上面定义中的“短期”旨在将该定义与其他确定时钟源纯净度的方式相区别,例如每百万稳定点,即 ppm。后者通常在较长的一段时间测得,例如数秒或数分钟。
相位噪声通常以对数频率图表示,例如下图(图 1),图中幅度单位为 dBc/Hz(分贝与 1 Hz 带宽载波功率的比值)。x 轴表示相对于标称信号或“载波”频率的频率偏移。
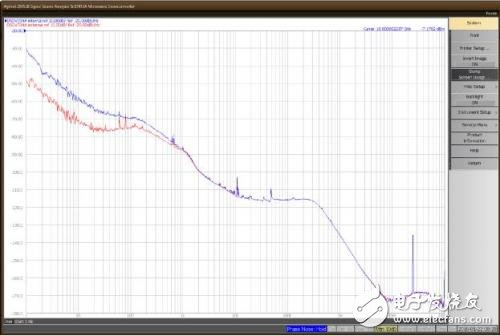
图 1
为什么使用示波器?
在说明如何使用示波器测量相位噪声之前,最好先了解一下为什么使用实时示波器。现在已经有了专门测量相位噪声的仪器,例如 Keysight E5052B 信号源分析仪(SSA),它拥有比任何示波器都低的相位噪声测量本底噪声。SSA 能够执行准确测量,更接近相位噪声偏移值,测量速度也比任何示波器都快。但是该仪器也有一些测量限制,例如对最大频率偏移范围有所要求。相位噪声分析仪的典型最大偏移为 100MHz。对大于 100 MHz 的时钟频率,有时也要测量更高的频率偏移,但这超出了此类仪器的测量范围。但示波器可以测量传递到数据信号上的相位噪声,而不仅仅测量时钟。
示波器使用简单如果也足以满足测量要求,当预算不足以购买专用的相位噪声测量设备时更是上佳选择。
相位提取
示波器可以捕捉整个信号波形并对其进行数字化,有多种方法可以从数字化波形中提取相位噪声信息。本文将简要介绍两种方法:
1、时钟恢复
2、通过矢量信号分析软件执行相位解调
通过串行数据时钟恢复执行相位解调
示波器分析信号是否达到设定的电压阈值,并将其与参考时钟边沿对比,从而测量串行数据或时钟信号的时序变化(抖动)。对于相位噪声,我们希望参考时钟为理想的固定频率时钟。大部分现代示波器都具有时钟恢复算法,可以从信号中提取时钟。在许多情况下,我们希望通过算法实现锁相环(PLL)仿真,但在这里,我们只需要提取一个固定周期的理想时钟,因此我们不会像 PLL 那样“追查出”任何相位变化。建立时钟恢复的示例如下图。(图 2)算法可设置为根据每次采样结果调整标称信号频率和相位。
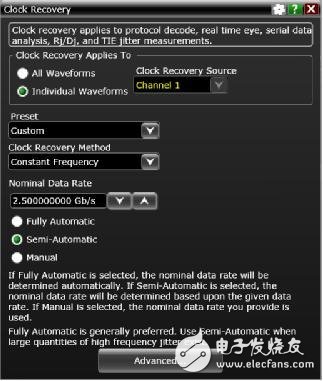
图 2
示波器对时间间隔误差(TIE)的测量能为每一个边沿相对理想时钟建立时序绝对时间误差。要转换至相位(弧度)误差我们只需要乘以2*pi*fc 即可,式中fc 为时钟载波频率。
φrad=2*π*TIEt*fc
时间间隔误差趋势可以通过 FFT 转换为频率空间,称为抖动频谱。大部分现代示波器均内置有此功能,或可通过选件实现此功能(图 3)。
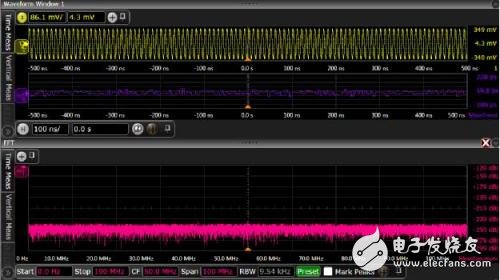
图 3
如需获取测得的相位谱密度清晰视图,需要对多次采样得到的抖动功率频谱进行平均化处理。
通过抖动频谱法得到的最大频率偏移值(fj_max)等于载波频率(当 TIE 包括上升和下降边沿时)。
最小频率偏移值(fj_min)在理论上由 TIE 采样的时间长度决定。即:采样得到的频率分量一定大于 TIE 第一个边沿与最后一个边沿之间时间的倒数。
#Pts=SaRatefφ_min
在这里通过实时采样示波器测量相位噪声存在困难。必须保持足够高的采样率才能准确测量到时间边沿,但为了得到低频率内容,必须使用非常大的采样存储器深度采集更长时间。
实例:
SaRate = 80 GSa/s
fj_min = 100Hz
所需存储深度= 800 MPts
每次采样都要通过时钟恢复、傅里叶变换建立抖动频谱的方式进行处理,找出边沿,然后对多次采样进行平均化。示波器必须具备深存储器,能够快速进行处理的能力。
现在我们了解了相位噪声测量的基础知识,但我们还是希望得到以 dBc/Hz 为单位的结果,因为这是此类测量的惯例。大部分相位噪声图都有对数频率刻度,可以更好地显示相近相位噪声偏移。
作为示例,我们以秒而不是弧度为单位建立 TIE 测量,然后将单位转换为 dBc,方法如下:
相位噪声 dBc= 20*log102*π*fc*jsrms(fφ)
但是请注意上面的相位噪声含有载波两边的能量。人们通常考虑的是单边带(SSB)相位噪声,即载波频谱单边带上的噪声,用符号 L 表示。因此我们必须将上面的相位噪声除以 2,因为 L(fj) = 0.5*Sφ(fj),还要除以抖动频谱解析带宽的平方根,以便将带宽标准化为 1 Hz。
因此:
L(fφ) dBc/Hzpk= 20*log10π*fc*jsrms(fφ)rbw
此类测量和转换的示例如下。(图 4)这里使用 Keysight Infiniium DSAV334A 示波器和一款名为 Infiniium 相位噪声的软件对高纯度 100MHz正弦波进行测量。不但要对抖动频谱进行平均化,还要在本次应用中使用平滑和杂散消除技术,从而更好地测量随机相位本底噪声。
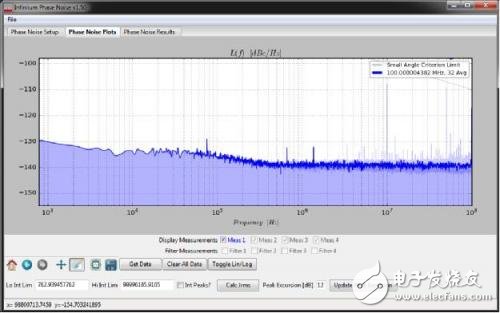
图 4
通过矢量信号分析软件执行相位解调
Keysight 89600B 等矢量信号分析软件可以使用包括实时示波器在内的多种硬件来获取数据。模拟相位解调算法对串行数据时钟恢复采用了不同的工作方法,但结果相似。
图 5 是一张高层次的方框图,描绘了 89600B VSA 软件如何执行相位解调。理想的本地振荡器(LO)以数学方法混合了数字化信号的 2 个副本,其中一个信号与另一个信号间有 90 度相位差。混合后的信号通过低通滤波消除高频混合产物,仅留下相位(和频率)误差。这可以用包括相位频谱在内的多种方式显示。
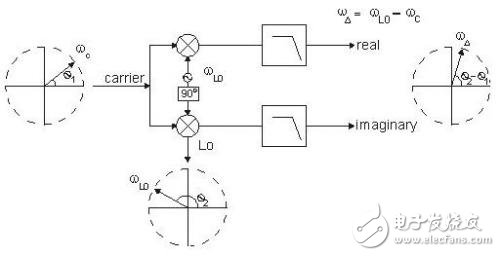
图 5
图中文字中英对照
VSA PM 解调算法可选配自动载波频率和相位追踪算法,如下图所示(图 6):
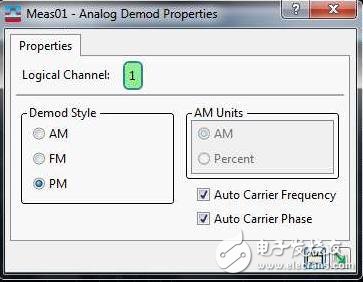
图 6
自动载波频率算法将时钟频率调整为测得的标称信号时钟频率,而不是用户输入值(类似串行数据时钟恢复)。这一频率会针对每一新的波形采集重新计算。
自动载波相位算法也会对每次采集的输入信号标称相位进行调整。
下图显示的也是使用 DSAV334A 示波器对 100MHz 纯正弦波进行测量,但通过 VSA 软件控制示波器的采样、相位解调和相位噪声频谱平均化。两种解调技术的结果呈现了完美的一致性。
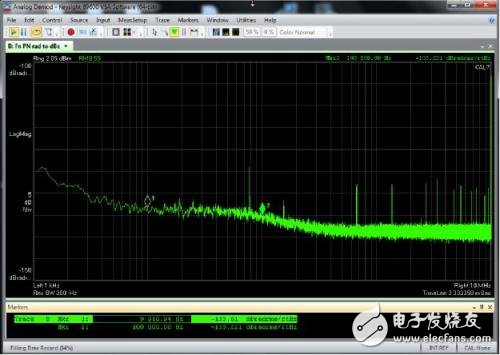
图 7
总结
可对实时示波器获得的数字化波形应用不同的算法来恢复相位噪声信息,建立相位噪声图。技术上的取舍不在本文讨论范围之内,但我们可以说使用示波器进行相位噪声测量不但可行,也非常有用。在后续文章中我们将讨论使用实时示波器进行此类测量时应作的权衡和如何保证精度。
-
安泰示波器维修分享--实时示波器和采样示波器的区别2018-04-26 0
-
采样示波器与实时示波器有什么区别?2019-08-02 0
-
残余相位噪声测量2011-11-24 1487
-
示波器是测量电源纹波和电源噪声的必备工具2018-03-12 19865
-
什么是实时示波器和采样示波器 他们各有什么优势2018-08-03 13535
-
采样示波器和实时示波器的对比和原理分析2018-08-03 15641
-
实时示波器与采样示波器区别2021-01-07 11695
-
脉冲载波相位噪声测量2022-11-21 375
-
示波器测量中的相位校正2023-05-12 2540
-
什么是示波器的实时采样率?什么是示波器的等效时间采样?2023-10-17 2076
-
示波器实时采样与等效采样有何区别2023-12-21 1042
-
采样示波器和实时示波器的区别2024-01-03 1364
-
普源示波器测量中的相位校正2024-01-09 704
-
等效时间采样示波器与实时示波器的对比,有什么不同?2024-01-19 1491
-
SXRTO(采样扩展实时示波器)的5W1H2024-11-21 179
全部0条评论

快来发表一下你的评论吧 !

