生物医学工程的电阻抗成像技术研究

电阻抗成像技术(Electrical Impedance Tomography， EIT)是当今生物医学工程重大研究课题之一，是继形态、结构成像之后，于八十年代出现的新一代有效的无损伤功能成像技术。本章主要介绍电阻抗成像技术理论，生物电阻抗测量系统原理以及生物电阻抗测量系统中弱信号检测技术理论，分析了常用的弱信号检测方法并介绍了阻抗测量中弱信号检测的噪声来源及处理方法。

2.1电阻抗成像技术

电阻抗成像是一种基于传统CT思想，以人体内部电阻率(电导率)的分布为成像目标的新型医学成像技术，它是一种廉价的无损伤探测技术。它不使用放射源，对人体无害，可作为对患者进行长期的、连续的监护的医学监护技术。它根据人体组织与器官的电特性(电阻率、电容率)，通过表面电极阵列施加激励电流或电压，测量边界电压或电流信号来获取物体内部电特性参数分布，进而重建物体内部结构与功能特性图像。因为人体不同组织和器官的电特性不同，这种EIT图像不仅包含了丰富的解剖学信息，而且可以获得与组织和器官电特性相应的生理、病理状态和功能信息，在研究人体组织与器官功能变化和疾病诊断方面有重要的临床价值。

EIT的主要研究问题有：EIT正问题、逆问题计算和硬件系统设计。硬件系统设计主要由三部分组成，电极阵列传感器、数据采集和图像重建计算机。传感器将多相流体分布转换成输出电极，数据采集系统将电极值转化为数字量并传送给计算机，计算机根据图像重建算法重建出被测物体的介质分布。

电阻抗断层成像EIT的目标是检测组织电特性的差异从而产生断层图像。EIT检测出来的组织电特性的信息是其它成像手段所不能够检测的，这样可能就会揭开一些其它检测手段所不能够提供的重要临床医疗信息。它注入人体电流的幅度和频率都比较低，与其他检测手段如x射线、CT、核磁共振(MRI)相比，具有对人体无创无害、设备成本低廉、成像速度快捷、使用安全和携带方便的优点。

人体可以看作是一个包含大量的具有不同电特性和不同空间分布的组织构成的复杂的导体。人体不同部位不同器官不同的组织具有不同的构成特点和组成成份，表现出相应的阻抗特性，它们之间的差异也非常明显。而且组织的阻抗与施加信号的频率有直接的关系。表2.l和表2.2给出了不同离体组织在不同频率下的电阻率和介电常数。

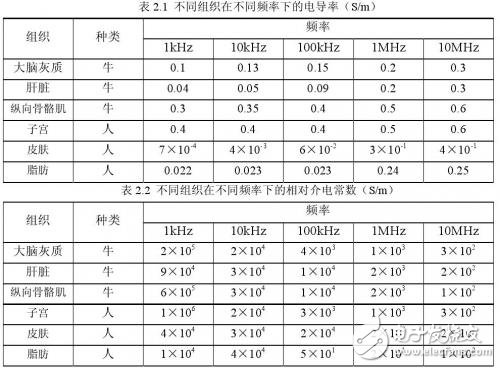
从表2.1和表2.2可以看出，频率越高，生物组织的电导率越大，相对介电常数越小。EIT技术也在往高速高精度发展，系统中采样速度和精度是最关键的因素。

2.2弱信号检测方法

微弱信号检测是EIT系统的前端处理技术，通过前端检测预处理，不至于使有用信号淹没于噪声之中，更有利于获取有用的信号。整个EIT系统精度随之提高，性能同时也得到较大的改善。

2.2.1典型的阻抗测量系统原理

经历了近20年的发展，EIT成了一个有一定基础的研究领域。各研究机构也相继推出各自的研究方法与系统。大多数研究机构都是通过在人体成像部位周围布置电极，将信号源通过电流施加到人体成像部位，同时测量边界电压或电流，通过各种方法获得或存储分析测得传输复阻抗数据，利用这些数据通过重建算法进一步处理成像。其原理如图2.1所示。

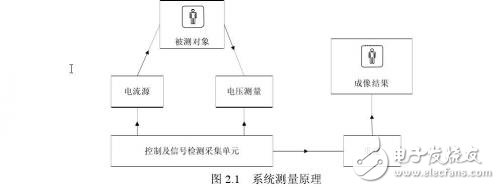
系统中控制及信号检测采集单元常常是硬件设计的核心，这个关键因素直接影响后期算法重建及成像结果。给信号检测与采集提供良好的前端信号正是本文研究的重点之一。

2.2.2典型的前端弱信号检测系统原理

典型的前端信号采集的硬件电路主要包括采集电极、放大滤波电路和AD变换。依据生物肌体的电特性和采集技术的基本要求，生物肌体所反馈回来的电信号非常微弱，分布在mV级和μV级。因此，需要对微弱信号进行放大，放大后才能达到AD采集单元的要求。典型的微弱信号检测调理组成框图如图2.2所示，前端检测预处理模块的设计包括以下几个部分：电极传感器、电压/电流测量放大、前置放大、ADC转换电路等。

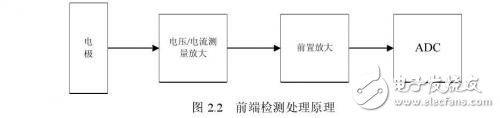
数据采集技术是信息获取过程中的关键技术，是模拟世界到数字世界的桥梁。

数据采集技术作为信息技术的重要组成部分，已经广泛应用于国民经济和国防建设各个领域，随着科学技术的发展，尤其是计算机技术的发展和普及，数据采集技术有着广泛的发展前景。

微弱信号检测作为数据采集的前端工作，直接影响数据采集的采样精度和采样速度。在生物电阻抗测量中，数据采集有其特殊性，由于生物肌体本身就是电导体，工频干扰和体外的电场、磁场感应都会在人体内形成测量噪声，干扰信号检测，因此，微弱信号检测就成了整个系统研究的重点之一。

2.2.3阻抗测量中弱信号检测的噪声来源

在生物弱信号检测过程中，由于实际工作情况并非理想状态，检测信号中往往含有很强的背景噪声。这些噪声既包括肌电噪声、呼吸波噪声、脑电噪声、心电噪声等生物噪声，同时也有工频噪声、电路板内部噪声、共模噪声等电噪声。

噪声对于弱信号检测，几乎是无处不在无处没有的，它总是与信号共存的。在传统检测方法中，总是千方百计的通过抑制噪声来检测有用信号，然而抑制噪声同时，难免会引起信号受到衰减和损失，因此，怎么处理这个矛盾常常是研究人员需解决的问题。

一般认为，信号是确定的，是时间的函数，我们能够事先计算且测量出它在某一时刻的值。在实际的信号检测中，信号常常伴随有噪声或其他干扰。

由于生物医学的特殊性，传感器的输出信号通常都很微弱，并且淹没在强噪声背景中，从而噪声成为信号检测的主要问题。微弱信号检测的目的是将信号和噪声区分，把淹没与噪声中的信号提取恢复。在信号检测系统中，可以处理的最高信号电平受电路特性的限制，但最小可检测的电平取决于噪声，即噪声限制了系统的动态范围和传感器的分辨率。对于生物电阻抗测量系统来说，更是如此。生物电阻抗测量中的噪声包括两个部分，一部分是由生物肌体自身阻抗等特性带来的干扰，它通过传感器、电极接触面和个人自身个体差异形成噪声；另一部分是由电路中的随机扰动产生的电噪声。

2.2.3.1生物肌体噪声

电源激励信号的幅值小、噪声强。因此，能否有效去除微弱的电源激励信号中的噪声并提取其特征信息对电源激励信号的研究和临床应用具有重要意义。生物的脑电、心电、肌电都会成为噪声产生的原因。脑电是人脑神经元突触后电位的综合结果，是脑神经细胞电生理活动在大脑皮层或头皮表面的总体反映[20]。在不受外界刺激的自然状态下，人脑产生的自发脑电信号一般被看做是非平稳比较突出的随机信号。生物本身的心电和肌电信号是人体在自然状态下产生的类似周期性的信号，也会引起噪声。

2.2.3.2电噪声

检测中的电噪声主要是由检测系统内部噪声引起，由电阻和各种器件产生的。绝大多数的电噪声是一个连续型随机变量，是一种前后独立的平稳随机过程，在任何时刻，它的幅度、相位以及波形都是随机的，但还是服从于一定的统计分布规律。

电阻热噪声是由电阻内部自由电子的热运动而产生的。起伏电流，电阻中的带电微粒(自由电子)在一定温度下受到热激发后，在导体内部作无规则的运动(热骚动)而相互碰撞，两次碰撞之间进行时，就产生一持续时间很短的脉冲电流。许多这样的随机热骚动电子所产生的这种脉冲电流组合，就在电阻内部形成了无规律的电流。在一足够长的时间内，其电流的平均值等于零，而瞬时值就在平均值上下变动。当实际电路中包含多个电阻时，每一个电阻都将引入一个噪声源。一般若有多个电阻并联时，总噪声电流等于各个电导所产生的噪声电流的均方值相加。

2.3常用弱信号检测算法

生物弱信号的特点是幅度小，往往淹没在噪声之中。为了检测被背景噪声覆盖的微弱信号，人们进行了长期的研究工作，分析噪声产生原因及规律，研究被测信号的特点、相关性及噪声的统计特性，以寻找从背景噪声中检测出有用信号的方法。常用的微弱信号检测方法有：相干检测法、基于混沌振子的微弱信号检测、同步累积法、双路消噪法、窄带滤波法等。

2.3.1相干检测法

相关接收技术是应用信号周期性和噪声随机性的特点，通过自相关或互相关运算，达到去除噪声、检测出信号的一种技术[13][15]。由于信号和噪声是相互独立的过程，根据相关函数和互相关函数定义，信号只与信号本身相关，与噪声不相关，而噪声之间一般也不相关。

2.3.1.1自相关检测

实现自相关检测的原理框图[13]如图2.3所示。

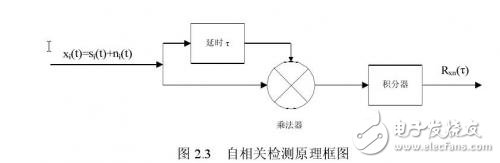
设输入x i(t)由被测信号s i(t)和噪声n i(t)组成，即：

x i(t)同时输入到相关接收机两个通道，其中一路将经过延时器，使它迟延一段时间τ。经过迟延的x i(t-τ)和未经迟延的x i(t)均送入乘法器内，再将其乘积积分，然后输出平均值，从而得到相关函数上一点的相关值。如果变更迟延时间τ，重复上述计算就能得到相关函数R xx(τ)与τ的关系曲线，即得自相关的输出为：

根据互相关函数性质，由于信号s(t)与噪声n(t)不相关，并且噪声的平均值为零，得到R sn(τ)=0，R ns(τ)=0，则R xx(τ)= R ss(τ) +R nn(τ)。随着τ的增大，R nn(τ)→0，则对充分大的τ，可得R xx(τ)= R ss(τ)。这样就得到了信号s i(t)的自相关函数R xx(τ)，它将包含着s i(t)所携带的某些信息。

随着时间τ的增加，噪声的自相关函数迅速衰减，而信号的自相关函数是小衰减的周期函数，从而可检测出有用信号。

2.3.1.2互相关检测

如果发送信号的重复周期或频率已知，就可在接收端发出一路重复周期与发送信号相同的本地信号，将本地信号与混有噪声的输入信号进行互相关。如图2.4是实现互相关检测的原理框图，设输入x(t)为：x (t ) = s (t ) +n (t )

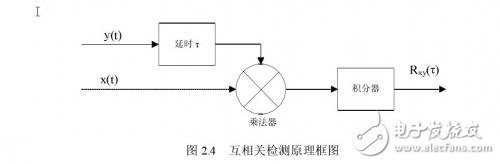
s(t)为待测信号，n(t)为信号s(t)中混入的噪声，y(t)为己知参考信号，若y(t)与信号s(t)有相关性，而与噪声n(t)无相关性，输入经延时、相乘、积分及平均运算后，得到互相关输出R xy(τ)为

由于参考信号y(t)与信号s(t)有某种相关性，而y(t)与噪声n(t)没有相关性，且噪声的平均值为零，则有R ny(τ)=0，即：