

平面低通滤波器的简介与设计方法解析
电子说
描述
1.平面低通滤波器简介
随着现在微波链路越来越高频化,小型化,直接在链路中集成低通的现象越来越普遍。同时很多芯片化的低通也大都是在高介电陶瓷片上实现的微带滤波器。陶瓷片型的芯片电容,电感,均衡器都需要用到平面低通的设计概念。
常见的低通滤波器在ADS中的模型及结构形式见图1。
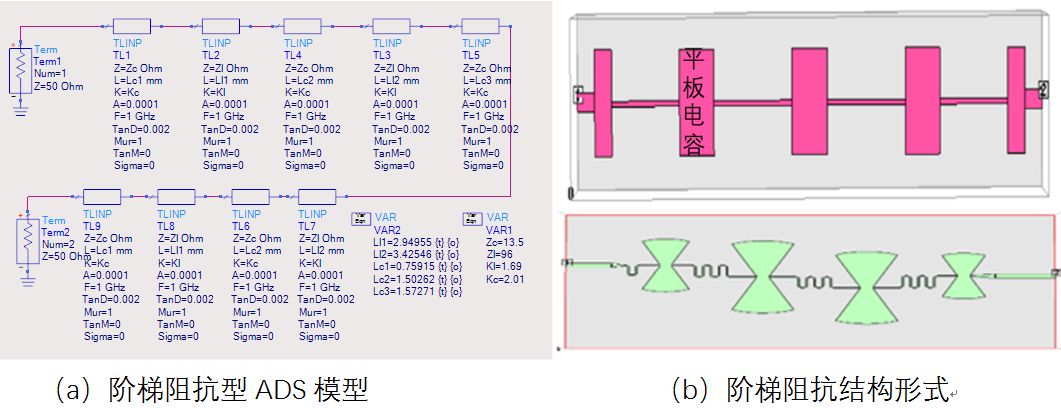
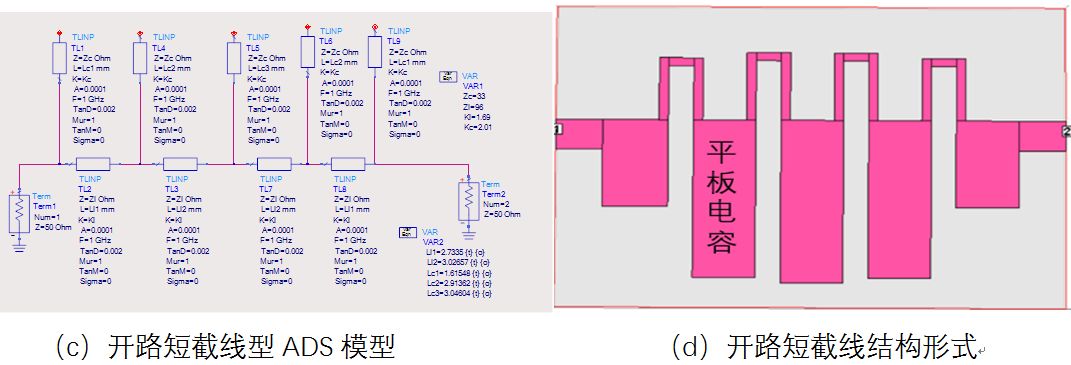
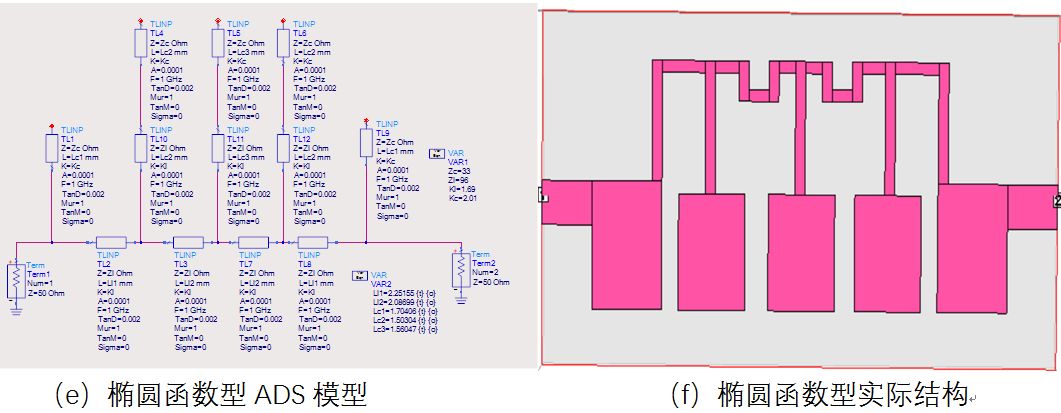
图1 常见的平面结构低通滤波器
三种结构的优缺点对比见表 1,通常对要求比较高的设计时可综合三种结构的优缺点进行折中设计。
表 1 三种结构优缺点对比
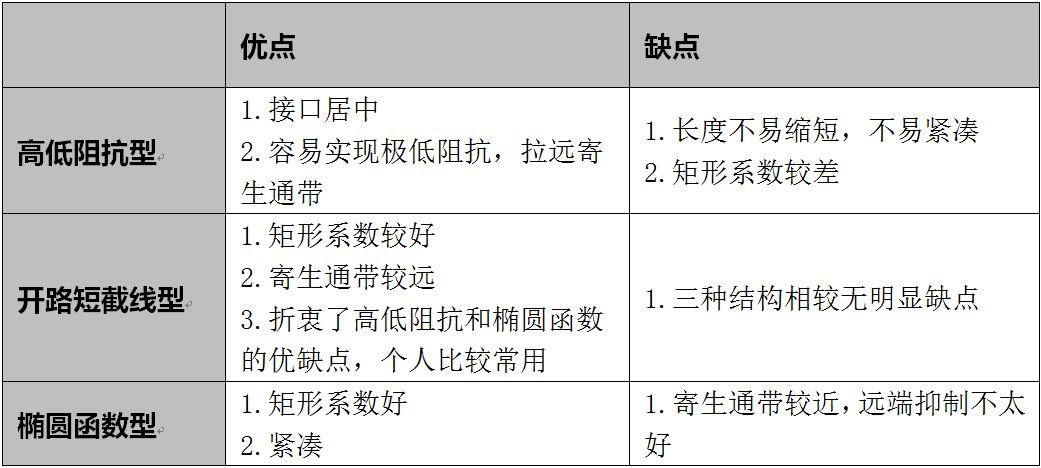
2.平面低通滤波器设计的理论基础
本次总结的理论基础来源于《Microstrip Filters for RF and Microwave Applications 2001》第4/5章,核心理论为图2的高低阻抗线等效电路。结论是:一段高阻抗线可以等效为电感,一段低阻抗线等效为一个到地电容。(如果理解传输线的特征阻抗用微分形式的集总参数表示为sqrt(L/C),高阻L一定很大,低阻C一定很大,就可以比较形象的理解此等效原理。)
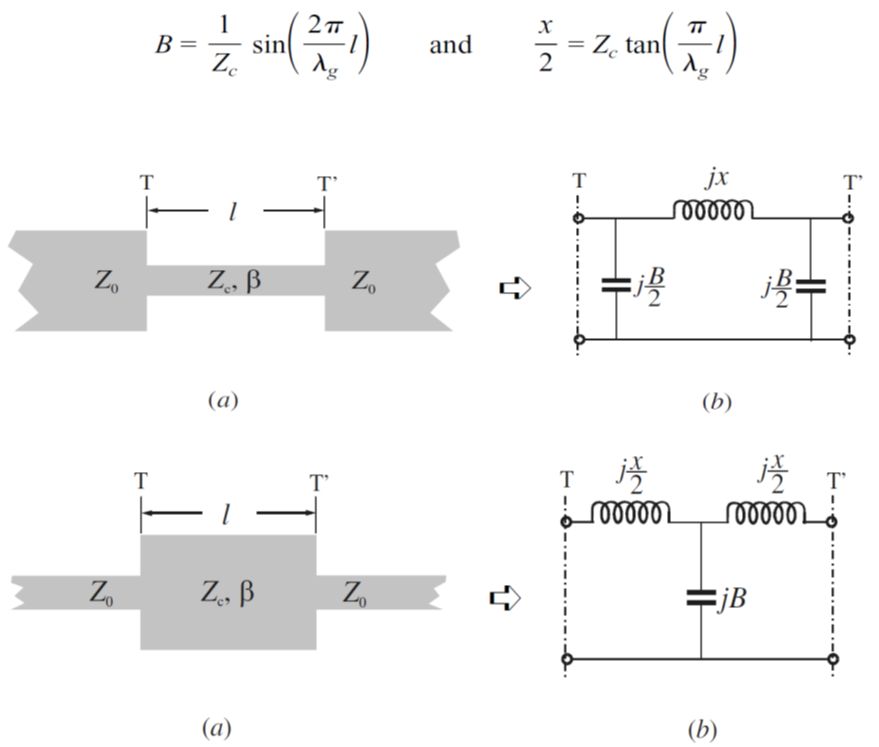
图2 高低阻抗线等效电路
3.平面低通设计实列
一个平面低通遵循下列设计步骤。
1)规划高低阻抗线阻抗,高阻受限于线条加工能力和功率容量,一般小功率应用可以取到0.15mm,低阻宽度受到滤波器尺寸限制,受到长宽比限制。(一般高低阻抗比例越大,寄生通带越远,但寄生通带远也意味着近端抑制会差,所以设计时可灵活配置各枝节阻抗,达到寄生通带和矩形系数的均衡)
2)ADS建模仿真获取初始电磁仿真参数
3)电磁仿真验证优化
本例用一个10GHz的平面低通作为实例,为了方便采用混合结构形式。
1) 规划高低阻抗线
高低阻抗规划要折衷级数/尺寸以及电性能,在实际设计中有迭代过程。高低阻抗计算有很多工具,这里推荐一个:polar SI9000(可以百度自行搜索),传输线特性参数计算非常实用的工具。本例中高阻选取加工极限0.15mm,低阻折中尺寸和寄生通带选取1mm宽,通过图 3计算可以得到1mm线宽的特性参数(特征阻抗和有效介电常数)为:W=1mm Z=33欧 Er=(2.98/2.16)^2=1.90 (光速比相速的平方)W=0.15mm Z=96欧 Er=1.69
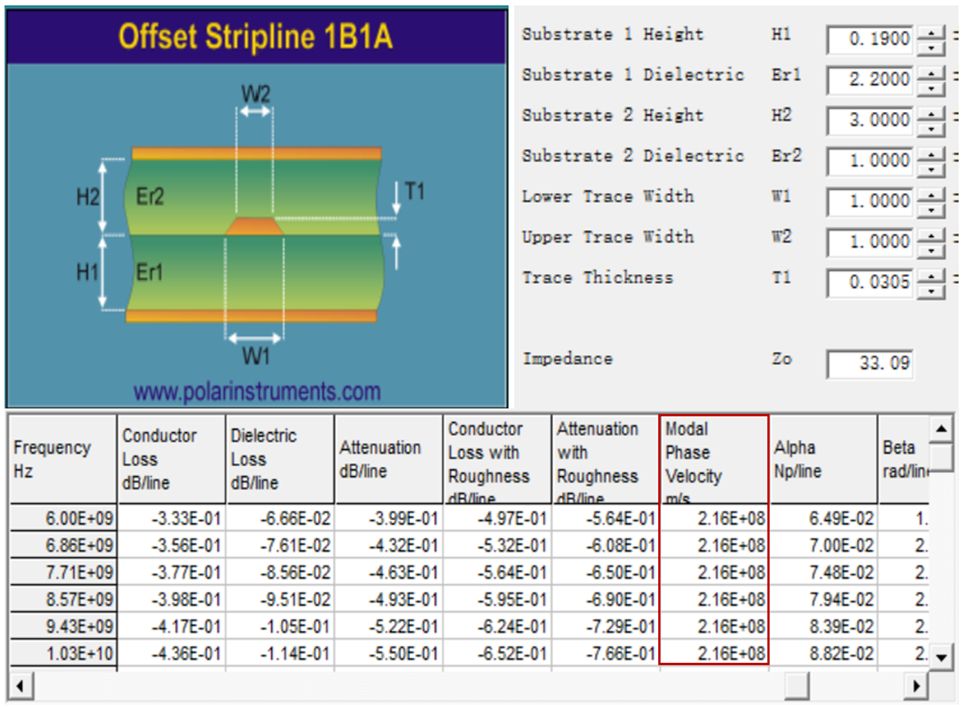
图3 传输线阻抗计算
2) ADS建模
在ADS中建立由高低阻抗传输线级联的理想电路模型,获取电磁仿真的初始参数,个人习惯采用ADS中Tline-ideal中的TlineP,该模型有三个参数:阻抗/有效介电常数/长度,前两个参数在高低阻抗线规划中已经获得,模型建模时只有物理长度一个变量,可以用1/8波长作为初始值,然后通过ADS中的优化快速获取准确的物理长度。详细的模型见图 4。
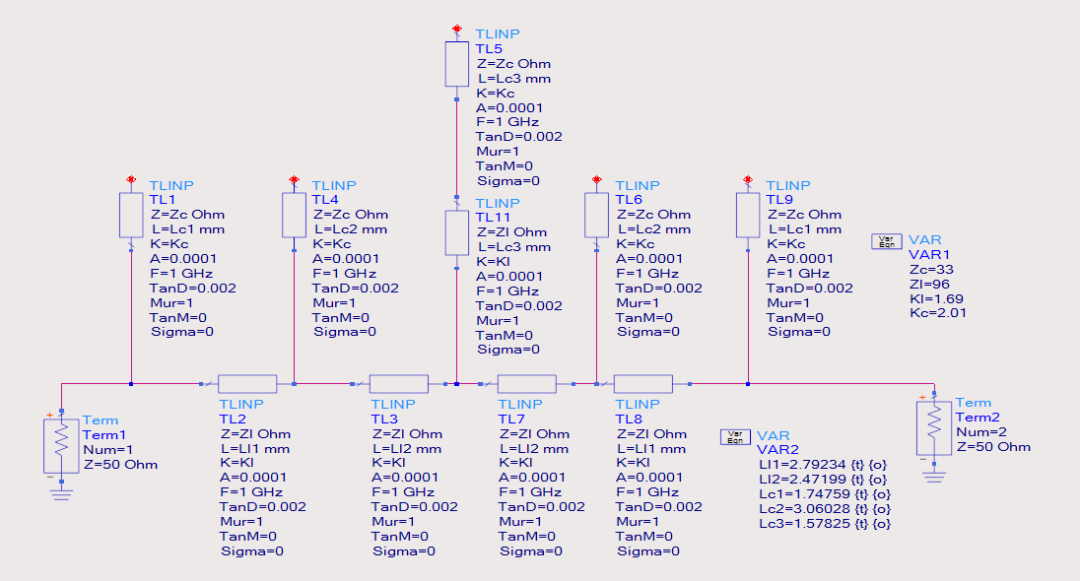
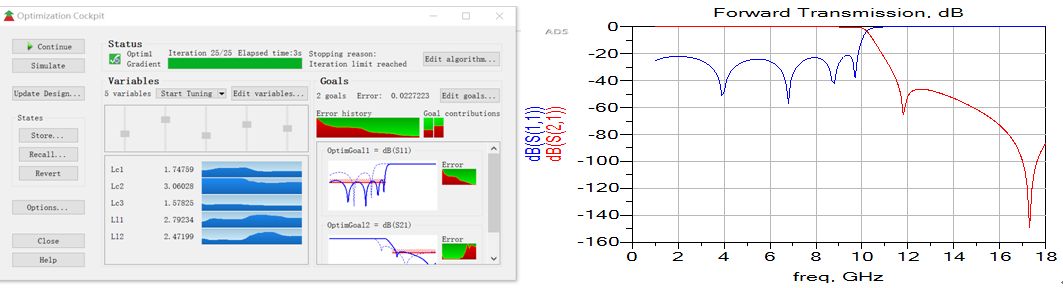
图4 ADS模型优化获取电磁仿真尺寸
3) Sonnet电磁仿真
所有平面结构的微波器件个人习惯使用sonnet进行仿真,sonnet可以随意更改结构形状,很接近实际调试时采用的方法,并且仿真速度非常快,很适合平面结构的电磁仿真。
在sonnet中根据ADS仿真中获取的尺寸建立初始电磁仿真模型如图 5所示。
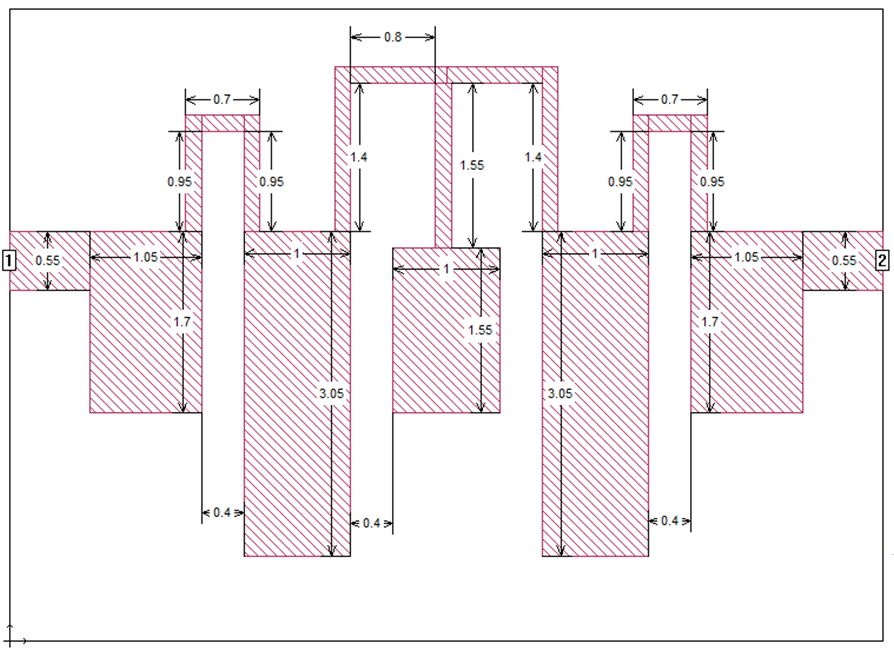
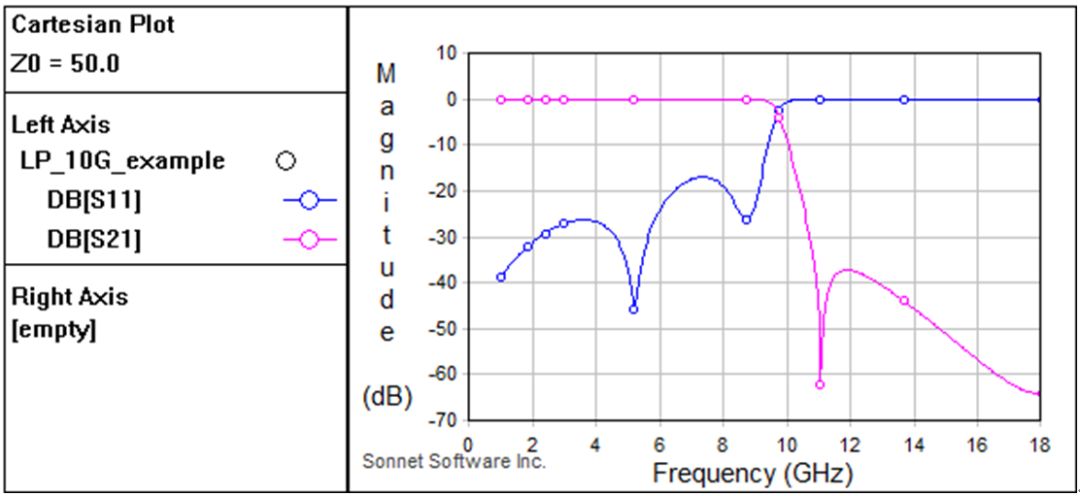
图5 sonnet第一次电磁仿真结构和结果
通过电磁仿真可以发现ADS模型中给出的参数已经非常准确了,在电磁仿真时基本不需要优化了。
但ADS中的模型毕竟不能模拟各个短截线间的耦合效应,接头不连续效应,根据经验通常只需要微调下高阻线的长度就可以得到很好的设计结果了。
-
低通滤波器的常见误区2025-01-21 1268
-
模拟低通滤波器的设计方法有哪些2024-11-26 2278
-
高通滤波器和低通滤波器判别方法2024-07-15 2841
-
什么是低通滤波器?低通滤波器有什么作用?2024-04-08 6809
-
高通滤波器、低通滤波器、带通滤波器怎样测幅频特性?2024-03-28 7870
-
低通滤波器电路图分享2024-02-12 9614
-
如何判断高通滤波器和低通滤波器2023-06-26 6167
-
低通滤波器与高通滤波器有什么不同2023-02-17 15640
-
LTCC低通滤波器的设计解析2020-09-18 8474
-
平面低通滤波器设计介绍2019-07-05 2638
-
LC低通滤波器作用及应用案例2016-10-09 42284
-
低通滤波器如何设计?2011-11-07 10960
-
有源滤波器中数字低通滤波器的设计及其DSP实现2010-05-13 982
-
低通滤波器设计2008-12-01 4782
全部0条评论

快来发表一下你的评论吧 !

