浅谈COT控制BuckBuck为什么是天然稳定的？稳定条件是什么？

COT 稳压器不需要环路补偿，但是他能提供优异的瞬态性能。COT可以使用常规定频 DC-DC 系统 1/2 甚至 1/4 的小电感，输出电压 Ripple 控制。但是PART2 CCM下，COT控制的Buck为什么不稳定？本文讲解COT控制的Buck的稳定条件。

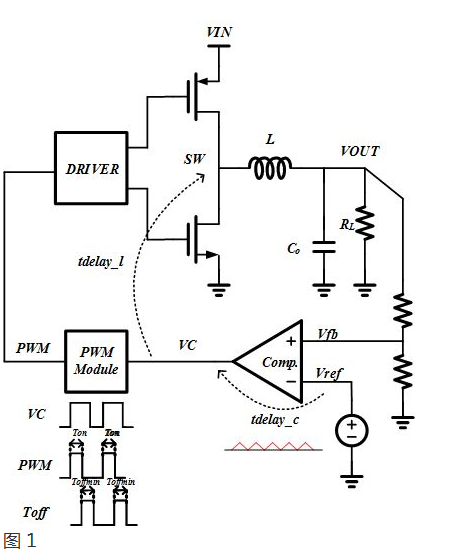
图1是COT控制的Buck的整体框图。

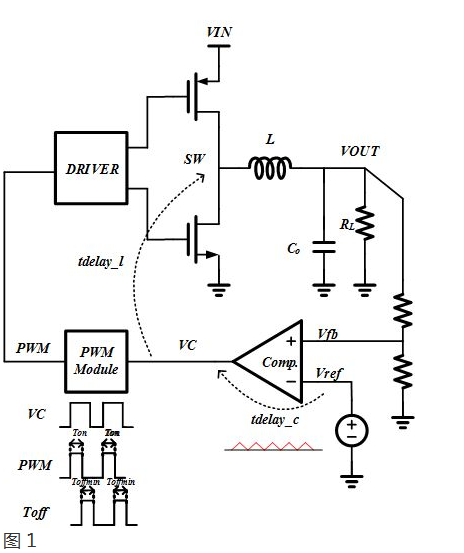
它的基本控制逻辑如图2所示。当反馈电压低于基准电压的时候，上边开关管打开，SW点变高，输出能量，让VOUT停止下降并上升；经过Ton时间之后，上边开关管关闭，下边开关管打开，SW点变低，让VOUT停止上升并下降。当VOUT下降到一定程度，即反馈电压低于基准电压，重新让SW点变高，如此循环。

这个基本控制逻辑是不完整的，SW变高Ton时间之后，如果输出不足够高，导致反馈电压仍然低于基准电压怎么办？所以需要引入一个额外的逻辑：

当上边开关管关断时（SW变高ton时间之后），如果反馈电压仍然低于基准电压，则上边功率管关断Toffmin时间之后重新打开。

事实上这个额外的逻辑并不这样做，而是：

当SW变高Ton时间之后，上边开关管强制关断Toffmin时间，Toffmin时间之后，如果反馈电压仍然低于基准电压，则上边开关管重新打开。

（大家可以对比一下两者有什么不同？）

这就是COT控制的Buck的控制逻辑。如果要跟其他控制模式进行对比的话，简单地，大家可以思考上边开关管打开和关闭的条件分别是什么就可以了。比如说定频的电压模控制的Buck，上边功率管什么时候开？时钟来的时候开（或者锯齿波快速下降的边沿）；上边功率管什么时候关？反馈电压高于基准电压的时候关。

PART2 CCM下，COT控制的Buck为什么不稳定？

COT控制下的Buck不存在输出电压会飘得很高，或者直接拉低的不稳定（不会出现正反馈的情况）。COT控制下的Buck主要会存在次谐波震荡（subharmonic oscillation）的不稳定情况。

如果COT控制下的Buck不存在次谐波震荡的问题，则开关管的打开关闭完全由基本控制逻辑控制（图2），上述“额外的逻辑”并不决定上边开关管何时打开，也就是说上边功率管关断的时间肯定大于Toffmin时间。

如果COT控制下的Buck存在次谐波震荡的问题，则会存在，SW变高Ton时间，变低Toffmin，再变高Ton时间，再变低Toffmin，如此几个周期之后，SW较长一段时间变低（》Toffmin时间），然后在变高Ton，再变低Toffmin，如此循环。如图3所示。

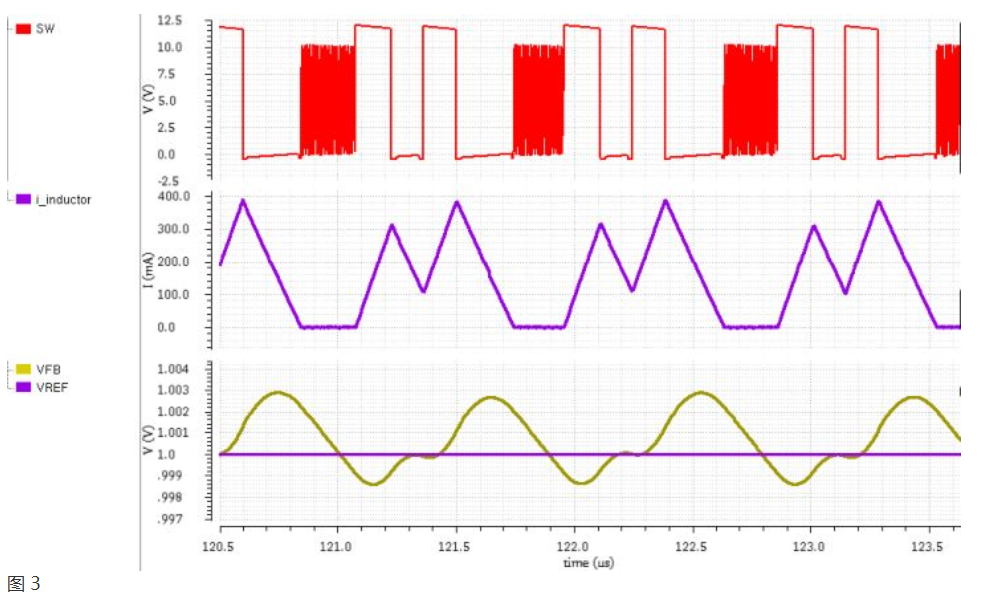
先给出结论1：CCM下的COT控制Buck如果没有任何补偿（包括电容没有ESR），且Toffmin非常非常小，几乎等于0的情况下，肯定是会出现次谐波震荡的问题。

论证逻辑是：如果不存在次谐波震荡问题，则肯定会存在一个稳定的状态。我们画出这个稳定状态，并证明它不符合控制逻辑就好了。

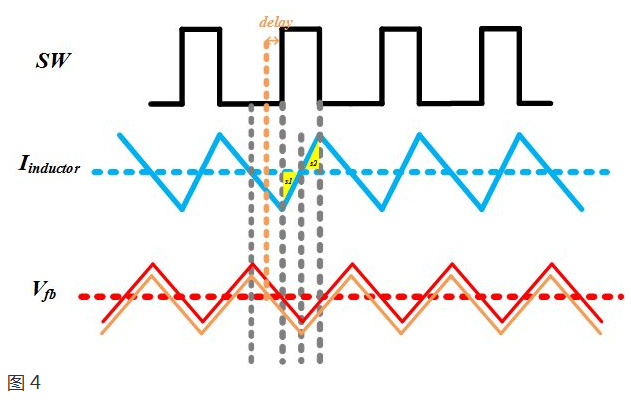
如果存在一个稳定的状态，则肯定如图4所示。最上面尾SW点的电压波形；中间尾电感电流波形，虚线为负载电流；最下面的红色波形为理想情况下的反馈电压波形，虚线为基准电压，橘黄色尾存在延迟情况下的波形。

理想情况下，反馈电压低于基准电压，SW翻高，并维持Ton时间。这段时间之内，电感电流上升，Buck输出的电容充放电电荷量恰好等于图中三角形S2的面积减去S1的面积。稳定情况下，这段时间内充放电电荷量恰好为零。这就意味着，SW翻高Ton时间之后，反馈电压恰好等于基准电压。如果存在一定的delay（如图橘黄色的波形所示），系统肯定会认为此时反馈电压仍然低于基准电压，根据COT的控制逻辑（此时假设Toffmin很小），SW会关断Toffmin时间之后再开一个Ton时间，而不会如图4般稳定输出。所以图4假设的稳定波形肯定不存在，结论得到证明。

再给出一个结论，Toffmin变大确实可以让次谐波震荡消失。（这时候再体会一下我给出的额外的逻辑的两种描述有什么区别。）

PART3 DCM下，COT控制的Buck为什么是天然稳定的？

分析方法和CCM下类似，基本上是看图说话。

先给出结论2，DCM下，如果延迟不是很大的情况下，COT控制的Buck是天然稳定的。

证明这个结论的逻辑是：先给出一个稳定的状态，证明这种状态是存在的；然后证明出现一个扰动的情况下，会回到这种状态。

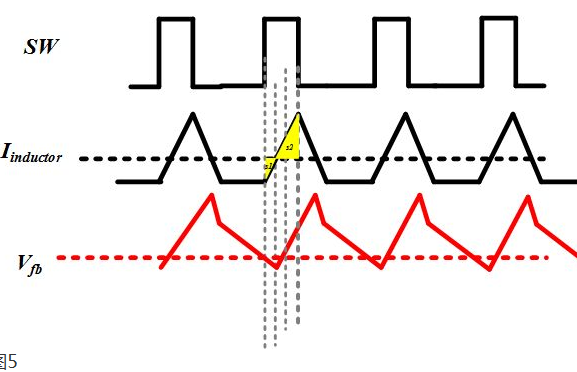
稳定状态如图5所示。DCM模式下，S2的面积肯定大于S1面积，意味着当SW维持Ton之后，反馈电压已经高于基准电压了，此时不会额外的逻辑不起作用，所以不存在次谐波震荡的问题。

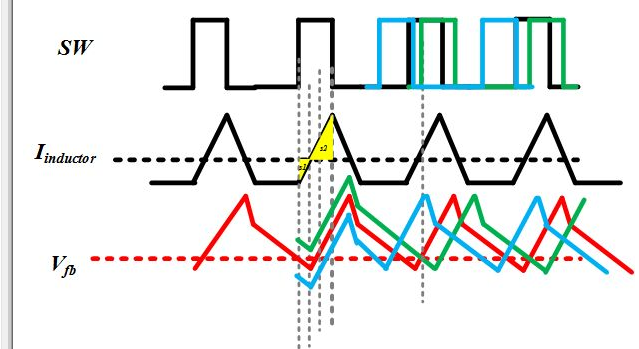
如果出现一个扰动，如图6所示。绿色线为在SW变高时刻（为了方便，随便找的一个时刻），输出出现向上扰动时的波形；蓝色线为在SW变高时刻，输出出现向下扰动时的波形。可以观察得到，对于这种扰动，都在一个周期之内就恢复到了稳定状态，这就说明了，其他状态都收敛于这个稳定态，由此证明了结论2。

PART4 DCM下，COT控制的Buck的稳定条件

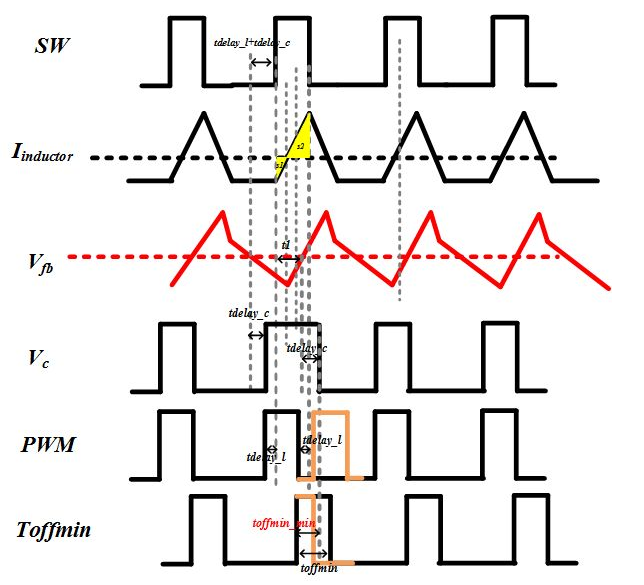
这一部分是定量的计算，没兴趣可以不看。根据图1的拓扑，PWM波的输出逻辑由PWM Module模块控制。实际输出的PWM波到SW翻转存在一个tdelay_l的延迟。tdelay_c比较器的延迟。图7是波形的分析。VC为比较器输出，PWM为PWM Module的输出。Toffmin尾PWM Module的内部控制波形。

PWM波翻高的逻辑是：Toffmin=0&Vc=1；PWM波翻低的逻辑是：翻高Ton时间之后自然翻低。

由图可知，如果toffmin小于toffmin_min，则PWM就会在变低Toffmin之后马上开启，导致次谐波震荡的发生（如图橘黄色波形所示）。因此稳定的条件是：

toffmin_min和tdelay之间的关系。而这就是DCM情况下，COT控制Buck的稳定条件。