蚁群算法是什么能做什么_蚁群算法的优势在哪里？

蚁群算法是什么

蚁群算法是一种群智能算法，也是启发式算法。基本原理来源于自然界蚂蚁觅食的最短路径原理。

（一）蚁群算法的由来

蚁群算法最早是由Marco Dorigo等人在1991年提出，他们在研究新型算法的过程中，发现蚁群在寻找食物时，通过分泌一种称为信息素的生物激素交流觅食信息从而能快速的找到目标，据此提出了基于信息正反馈原理的蚁群算法。

蚁群算法的基本思想来源于自然界蚂蚁觅食的最短路径原理，根据昆虫科学家的观察，发现自然界的蚂蚁虽然视觉不发达，但它们可以在没有任何提示的情况下找到从食物源到巢穴的最短路径，并在周围环境发生变化后，自适应地搜索新的最佳路径。

蚂蚁在寻找食物源的时候，能在其走过的路径上释放一种叫信息素的激素，使一定范围内的其他蚂蚁能够察觉到。当一些路径上通过的蚂蚁越来越多时，信息素也就越来越多，蚂蚁们选择这条路径的概率也就越高，结果导致这条路径上的信息素又增多，蚂蚁走这条路的概率又增加，生生不息。这种选择过程被称为蚂蚁的自催化行为。对于单个蚂蚁来说，它并没有要寻找最短路径，只是根据概率选择；对于整个蚁群系统来说，它们却达到了寻找到最优路径的客观上的效果。这就是群体智能。

（二）蚁群算法能做什么

蚁群算法根据模拟蚂蚁寻找食物的最短路径行为来设计的仿生算法，因此一般而言，蚁群算法用来解决最短路径问题，并真的在旅行商问题（TSP，一个寻找最短路径的问题）上取得了比较好的成效。目前，也已渐渐应用到其他领域中去，在图着色问题、车辆调度问题、集成电路设计、通讯网络、数据聚类分析等方面都有所应用。

（三）蚁群算法的流程步骤

这里以TSP问题为例，算法设计的流程如下：

步骤1：对相关参数进行初始化，包括蚁群规模、信息素因子、启发函数因子、信息素挥发因子、信息素常数、最大迭代次数等，以及将数据读入程序，并进行预处理：比如将城市的坐标信息转换为城市间的距离矩阵。

步骤2：随机将蚂蚁放于不同出发点，对每个蚂蚁计算其下个访问城市，直到有蚂蚁访问完所有城市。

步骤3：计算各蚂蚁经过的路径长度Lk，记录当前迭代次数最优解，同时对路径上的信息素浓度进行更新。

步骤4：判断是否达到最大迭代次数，若否，返回步骤2；是，结束程序。

步骤5：输出结果，并根据需要输出寻优过程中的相关指标，如运行时间、收敛迭代次数等。

要用到的符号说明：

 

初始时刻蚂蚁被放在不同的城市，且各城市路径上的信息素浓度为0。

由于蚁群算法涉及到的参数蛮多的，且这些参数的选择对程序又都有一定的影响，所以选择合适的参数组合很重要。蚁群算法有个特点就是在寻优的过程中，带有一定的随机性，这种随机性主要体现在出发点的选择上。蚁群算法正是通过这个初始点的选择将全局寻优慢慢转化为局部寻优的。参数设定的关键就在于在“全局”和“局部”之间建立一个平衡点。

（四）蚁群算法的关键参数

在蚁群算法的发展中，关键参数的设定有一定的准则，一般来讲遵循以下几条：

尽可能在全局上搜索最优解，保证解的最优性；

算法尽快收敛，以节省寻优时间；

尽量反应客观存在的规律，以保证这类仿生算法的真实性。

蚁群算法中主要有下面几个参数需要设定：

（下面列的是一些书上的主要结论，实验过程就不举例了，具体参考《MATLAB在数学建模中的应用》）

蚂蚁数量：

设M表示城市数量，m表示蚂蚁数量。m的数量很重要，因为m过大时，会导致搜索过的路径上信息素变化趋于平均，这样就不好找出好的路径了；m过小时，易使未被搜索到的路径信息素减小到0，这样可能会出现早熟，没找到全局最优解。一般上，在时间等资源条件紧迫的情况下，蚂蚁数设定为城市数的1.5倍较稳妥。

信息素因子：

信息素因子反映了蚂蚁在移动过程中所积累的信息量在指导蚁群搜索中的相对重要程度，其值过大，蚂蚁选择以前走过的路径概率大，搜索随机性减弱；值过小，等同于贪婪算法，使搜索过早陷入局部最优。实验发现，信息素因子选择［1，4］区间，性能较好。

启发函数因子：

启发函数因子反映了启发式信息在指导蚁群搜索过程中的相对重要程度，其大小反映的是蚁群寻优过程中先验性和确定性因素的作用强度。过大时，虽然收敛速度会加快，但容易陷入局部最优；过小时，容易陷入随机搜索，找不到最优解。实验研究发现，当启发函数因子为［3，4.5］时，综合求解性能较好。

信息素挥发因子：

信息素挥发因子表示信息素的消失水平，它的大小直接关系到蚁群算法的全局搜索能力和收敛速度。实验发现，当属于［0.2，0.5］时，综合性能较好。

信息素常数：

这个参数为信息素强度，表示蚂蚁循环一周时释放在路径上的信息素总量，其作用是为了充分利用有向图上的全局信息反馈量，使算法在正反馈机制作用下以合理的演化速度搜索到全局最优解。值越大，蚂蚁在已遍历路径上的信息素积累越快，有助于快速收敛。实验发现，当值属于［10，1000］时，综合性能较好。

最大迭代次数：

最大迭代次数值过小，可能导致算法还没收敛就已结束；过大则会导致资源浪费。一般最大迭代次数可以取100到500次。一般来讲，建议先取200，然后根据执行程序查看算法收敛的轨迹来修改取值。

 

蚁群算法的优势在哪里？

图论中很多问题都是求某个规则下的最短路径，但因为规则不同，这些问题也有着本质上的不同，不能简单地都归于“最短路径”问题，某些问题已有有效算法，有些问题至今没有有效算法。

Prime 算法和 Kruskal 算法都是用来求加权连通简单图中权和最小的支撑树（即最小树）的，Prime算法的时间复杂度为O（n^2） （n 为顶点数），Kruskal 算法的时间复杂度为 O（eln（e）） （e为边数），这两种算法都是多项式时间算法，也就是说，最小树问题已经有了有效算法去求解，属于P问题。

Dijkstra 算法求解的是加权连通简单图中一个顶点到其它每个顶点的具有最小权和的有向路，最简单版本的时间复杂度是O（n^2），也是多项式时间算法。

而蚁群算法是一种近似算法，它不是用来解决已存在精确有效算法的问题的，而是用来解决至今没有找到精确的有效算法的问题的，比如旅行商问题（TSP）。

旅行商问题也可以说是求“最短路径”，但它是求一个完全图的最小哈密顿圈，这个问题至今未找到多项式时间算法，属于NPC问题，也就是说，当问题规模稍大一点，现有的精确算法的运算量就会急剧增加。

 

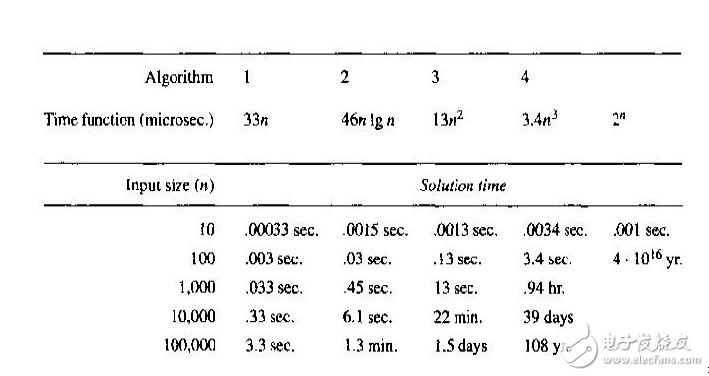
在上图中，可以看到，当问题规模为10时，复杂度为O（3.4n^3） 的算法运行时间要0.0034s，复杂度为O（2^n） 的算法运行时间要0.001s，此时相差还不大，但当问题规模增加到100时，前者的运行时间只是增加到了3.4s，而后者的运行时间则增加到了4×10^16年！

因为实际问题的规模都比较大，100还是小数字，所以对一个问题，都努力寻求多项式算法。但也有问题目前还没有找到多项式时间的精确算法，比如旅行商问题，因此就产生了各种近似算法，以解的质量来换取效率，寻求满意解而不是最优解，蚁群算法就是其中一种。

所以，针对本问题的提法，蚁群算法和Prime 算法或Kruskal 算法等是两个不同层面上的算法，基本没有比较的必要，但可以做辨析：

1、Prime 算法，Kruskal 算法，Dijkstra 算法都只是解决某一种问题的，这些问题有了这些算法，就没有必要使用蚁群算法。

2、蚁群算法可以用来解决一些尚未找到有效算法的问题，而且蚁群算法还是元启发式算法（Metaheuristic），是一种算法框架，可以在其基本思想上针对不同问题做改进从而应用到不同问题上去。

3、蚁群算法可以和其它近似算法相比较，而这些算法本身也根据问题的不同有较大的改进弹性。

*图片来源：Sara Baase， Allen Van Gelder，Computer Algorithms： Introduction to Design and Analysis，影印版第三版，高等教育出版社，2001 （第49页 图1.5）