人工智能之技术与算法

　　人工智能之技术与算法

　　这篇文章更类似于科普贴，它完全可以作为你学习人工智能的入门文章，我的目的是用通俗的语言概括人工智能领域的各项技术，从而让读者有个直观浅显的认识

　　随机（Random）

　　随机是智能的基础，人工智能的很多技术都需要用到随机，因此有必要把这个提到前面谈谈

　　一考虑基于C/C++，般我们都是使用的rand（）等函数实现随机，当然我们也有吊炸天的boost提供了各种分布范围的随机：

　　#include 《boost/random.hpp>

　　uniform_int《> distribution（1， 100） ;

　　mt19937 engine ;variate_generator《mt19937，uniform_int《> > myrandom （engine， distribution）;

　　// uniform_smallint：在小整数域内的均匀分布

　　// uniform_int：在整数域上的均匀分布

　　// uniform_01：在区间［0，1］上的实数连续均匀分布

　　// uniform_real：在区间［min，max］上的实数连续均匀分布

　　// bernoulli_distribution：伯努利分布

　　// binomial_distribution：二项分布

　　// cauchy_distribution：柯西（洛伦兹）分布

　　// gamma_distribution：伽马分布

　　// poisson_distribution：泊松分布

　　// geometric_distribution：几何分布

　　// triangle_distribution：三角分布

　　// exponential_distribution：指数分布

　　// normal_distribution：正态分布

　　// lognormal_distribution：对数正态分

　　// uniform_on_sphere：球面均匀分布

　　但是这个取到的数据都是伪随机数，或依靠系统时间，或依靠日期等，显然这个对于人工智能是不够的，我们需要真随机，C++11的std ：：random_device给了我们希望，如名这个的随机石使用的硬件，linux是读取dev/urandom硬件设备，但是windows居然还是调用的rand_s（）函数！这个没什么太多说的，买点专业硬件即可。

　　状态空间启发式搜索-A寻路算法（A* Search Algorithm）

　　A寻路算法是A*的退化，所以我不考虑说什么，当然如果你想学习A星，先学A是一个不错的选择，为此我特意写了一篇文章详细讲解各种寻路搜索策略http://blog.csdn.net/racaljk/article/details/18887881

　　状态空间启发式搜索-A星寻路算法（A* Search Algorithm）

　　其实这个标题是我自己写得到，原翻译显然没有”寻路“这两个字，因为A星算法包括但不仅限于存在于人工智能的寻路中，但是既然标题是人工智能，这样也无伤大雅，在说A*之前有必要说所深度优先搜索算法DFS和广度优先搜索算法BFS，假设一个map上面，有诸多障碍，目前机器人需要做的就是在这个有限的地图上没有其他信息支持，需要从起点出发找到终点，如上所说，这个地图里面的障碍时允许尝试的，如果我们使用深度有限算法，他会从起点出发走一条路并一直走下去，直到遇到障碍或者没有达成条件-到终点，于是返回重新走，显然他不会愚蠢到走与之前同样的错误路线，DFS比较耗时，但是如果成功了也就执行了这条路线（没有人为干扰的情况下），而BFS则在遇到障碍时就会向四周试探性的走几步，一旦试探成功就继续走，如此递归，直到成功（如果在有限的map下，且存在正确路径，则必然会成功），简单来说，我们的理论都是基于二叉树的条件下，BFS是沿着树的宽度进行完全变遍历，而DFS是沿着数的一条分支一直走下去，直到成功，A*结合这两个算法的优点，从而实现快速寻路

　　下面这个更直观：

　　假设这个是一个地图，左#表示起点，右#表示终点，@@表示障碍

　　00000000000

　　000000@0000

　　#0000@@000#

　　000000@0000

　　00000000000

　　如果用DFS他会像扫描仪一样从左至右扫描到终点，如果用DFS他会像扫描一样从中间向两边扫描扫描，而A*则结合这两个算法的优势，从而实现最快的寻路，关于A*算法的源码请自行百度

　　下面是一个A*的一个动画演示

　　 

　　D星寻路算法（Dynamic A* Search Algorithm）

　　顾名思义d*也就是动态A*寻路算法，区别仅在于A*是局限于A*是生成一条路就一直走下去，但实际情况下有很多突发情况，比如生成的那条路被堵了，就需要重新生成新的路线，这就需要D*了，D*也就是说动态生成A*路线。

　　状态机（Finite-State Machine）

　　FSM看似很高端，的确我当初也被吓着了，不过看了下面的内容就会觉得很简单，细分状态机分为有限状态机和模糊状态机，也加同步状态机和异步状态机，两种状态机的区别在于有限状态机在一个时段只能处于一种状态，而模糊（也即异步）状态机有一个权重值，根据这个权重值我们可以分配给不同的状态不同的权重，比如一个人，有限状态机允许人去喝水，模糊状态机允许80%去喝水，20%接水。你甚至可以理解为FSM是单线程，FμSM是多线程。有关状态机的资料可以参见：http://zh.wikipedia.org/wiki/%E6%9C%89%E9%99%90%E7%8A%B6%E6%80%81%E6%9C%BA

　　为了便于理解，现复制一下基本概念：

　　状态（State）指的是对象在其生命周期中的一种状况，处于某个特定状态中的对象必然会满足某些条件、执行某些动作或者是等待某些事件。

　　事件（Event）指的是在时间和空间上占有一定位置，并且对状态机来讲是有意义的那些事情。事件通常会引起状态的变迁，促使状态机从一种状态切换到另一种状态。

　　转换（Transition）指的是两个状态之间的一种关系，表明对象将在第一个状态中执行一定的动作，并将在某个事件发生同时某个特定条件满足时进入第二个状态。

　　动作（Action）指的是状态机中可以执行的那些原子操作，所谓原子操作指的是它们在运行的过程中不能被其他消息所中断，必须一直执行下去。

　　看不懂上面可以看下面：

　　 

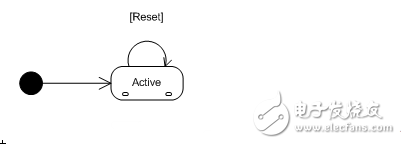
　　这里盗用一张UML（http://www.cnblogs.com/ywqu/archive/2009/12/17/1626043.html这是关于UML比较详细的介绍）图片来解释一下，黑圆圈表示初始状态，非规则长方形表示一个状态，Active表示状态条件，也就是这种状态需要什么条件，Reset表示转换事件

　　我们结合boost：：statechart可以很容易写出上述图片的代码

　　#include《boost/statechart/state_machine.hpp>

　　#include《boost/statechart/simple_state.hpp>

　　class Mchine_Initiate;//模板必须有一个class作为初始化后的状态

　　class Machine ： boost：：statechart：：state_machine《Machine， Mchine_Initiate>{

　　public：

　　Machine（）{std：：cout 《《 “Machine class”;};

　　};

　　class Mchine_Initiate{

　　public：

　　Mchine_Initiate（）{std：：cout 《《 “in”;};

　　~ Mchine_Initiate（）{std：：cout 《《 “out~”};

　　};

　　决策树（Decision Tree）

　　这个大家应该都不陌生，当我们遇到一个问题时会有多种处理方法，这符合一个树状态结构，

　　我们会选择最佳策略进行处理，同样，人工智能也有类似实现名为决策树，我们会发现者似乎与FSM有联系，恭喜你你的发现时正确的，这其实算是静态FSM，FSM应该冠名为动态FSM才是最佳的，当然这是我个人看法，何谓静态，就是既定的方案，这个树枝都有权重值，50%A树枝，50%B树枝，机器人可以按照这个既定的方案执行，因此决策树可以存储并分享，而FSM是动态选择，有关决策树的概念就这么多了，详细实现大家可以去百度一下。这里提供一篇算法，遗憾的是里面专业术语比较多，理解较困难。

　　博弈论（Game Theroy）

　　这是我最感喜欢的部分，某种程度上说没有博弈论体系的AI算不上AI，博弈论在人工智能中广泛用于最优化策略，从原英文中我们就看得出这个与游戏有关，对象是单体，著名的例子就是简化的囚徒困境：

　　两个囚徒甲和已违法被抓，分别关押，有如下选择：

　　如果两个人都承认，那么都判10年

　　如果一人不承认，另一人承认并指认同伙，那么这个人将无罪释放，而被指认的那个人将被判20年

　　如果两个人都不承认，将只是非法带枪罪判1年。

　　从单体出发，假设我是甲，我心里会想：如果我认罪，10年，不认罪20年，10《20，认罪最好。对方认罪我0年，对方不认罪1年，0《1认罪最后

　　以类同，因此选择认罪各10年

　　在人工智能中我们要穷举所有可能，并计算最终收益，最后让收益最大化，这就是人工智能的博弈论理论，博弈论博大精深，这里只是十分基础的认识

　　人工智能领域的博弈论我们需要考虑两个东西：期望收益、规则设定。比如我们的规则设定是机器人比赛，然后机器人要选择收益最大化，因此我们就要穷举各种可以执行的策略，并最终从这些策略对比使收益最大化，再如田忌赛马这个强拉硬扯算是博弈论，规则是上中下等马比赛，上>中，中>下，然后计算机就要穷举所有策略，优上>良上，优上>良中。..。，最终更加这些策略对比使收益最大化，我们可以把这些作为一个树状结构实现，称之为博弈树，博弈树广泛引用于各种棋牌游戏的AI，很多算法如alpha-beta搜索都是基于博弈树实现的

　　最大最小搜索算法（Max-min search algorithm）

　　最大最小搜索算法基于博弈树，广泛应用于棋盘较小的棋牌游戏AI中，详细请看我的文章http://blog.csdn.net/racaljk/article/details/18842545

　　神经网络（Artificial Neural Networks）

　　神经网络同上是人工智能的智能所在，神经网络类似于抽象了人类的历史，请不要反驳远古时期人类没有手机这句话，人类的聪明是经验所得，试想一下，假设机器人前面有一个障碍，这个障碍堵塞了路，机器人就会不断使用寻路算法尝试，显然，这是没有效果的，因为没有正确的道路，想想如果是你你会怎么做，你会跳过去，是的，这就是一个神经网络的实现，你早就经历过这种事情，现在你需要做的就是运用之前的经验来解决这个”新“情况。要想智能，没有这种经验的学习都是纸上谈兵（当然前提是你得置入跳的动作代码），当机器人用A*尝试5次都失败的情况下它就会改变策略，调整脚部神经元阀值，当调节为1，发现跳不过，就调节为8，如此在一定的区间内随机直到成功

　　置信网络（Belief Network）

　　从分类中可以看出置信网络从属于深度学习，而深度学习父级是神经网络，也就是说置信技术是以神经网络为基础的在其基础上优化的一门机器学习技术。

　　置信技术把人工智能推向了极致，他与博弈论、神经网络遗传算法构成了AI的核心体系。

　　之前我们的神经网络和遗传算法使用穷举进行尝试和筛选，而置信网络总结数据并试图发现规律，这看起来多麽伟大，同时也多麽不容易，把客观世界object的规律映射到智能机器，即使是人类也不一定做好

　　同样是上面走路的例子，我们假设了神经网络的阀值必须要是偶数*2才能通过，贝叶斯智信网络则是用来总结得出这个规律，他需要前面的数据并进行分析，并把抽象数据转化为客观规律

　　 

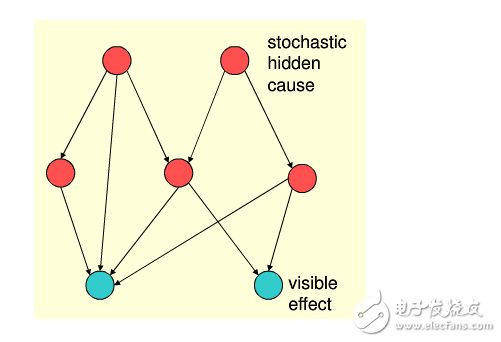
　　上图就是一个经典的置信网络，其中红色圆圈表示未知规律，蓝色为表象

　　置信网络可以极大优化神经网络，减少尝试次数，比如利用置信网络总结出结果在偶数*2中间，通过其他信息比如数量是家庭垃圾物体数，神经网络便可在一个较小的范围类进行偶数*2的尝试

　　遗传算法（Genetic Algorithm）

　　遗传算法的理论基础是达尔文的进化论，他模拟实现净化论中的自然选择和遗传机制，神经网络无法吸取上次失败的教训，只是一味的尝试，遗传算法由此而生解决这个问题，它吸取群体的智慧于一生，结合神经网络实现了更高层次的智能，遗传算法模拟培养第一代基因，神经网络进行尝试，然后进行优胜劣汰，如此递归，当到了一个很高的层次都无法解决问题的时候他就会考虑基因重组，也就是杂交，因为他认为第一代的优秀基因本身就是错误的方向，只是错误的方向上的优秀基因，因此他选择其他方向的基因用神经网络尝试，遗传算法优胜劣汰