常见算法优缺点比较

常见算法优缺点比较

机器学习算法数不胜数，要想找到一个合适的算法并不是一件简单的事情。通常在对精度要求较高的情况下，最好的方法便是通过交叉验证来对各个算法一一尝试，进行比较后再调整参数以确保每个算法都能达到最优解，并从优中择优。但是每次都进行这一操作不免过于繁琐，下面小编来分析下各个算法的优缺点，以助大家有针对性地进行选择，解决问题。

 

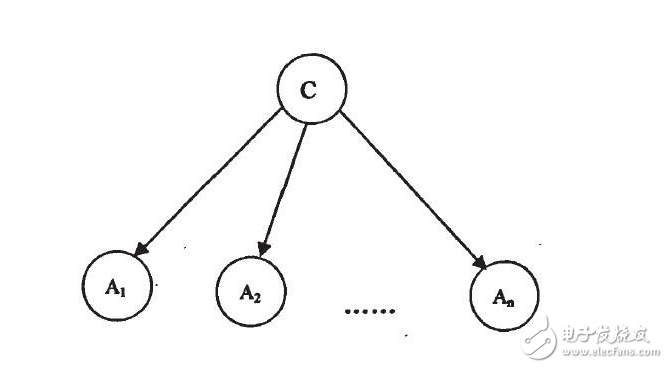
1.朴素贝叶斯

朴素贝叶斯的思想十分简单，对于给出的待分类项，求出在此项出现的条件下各个类别出现的概率，以概率大小确定分类项属于哪个类别。

优点：

1）朴素贝叶斯模型发源于古典数学理论，因此有着坚实的数学基础，以及稳定的分类效率；

2）算法较简单，常用于文本分类；

3）对小规模的数据表现很好，能够处理多分类任务，适合增量式训练。

缺点：

1）需要计算先验概率；

2）对输入数据的表达形式很敏感；

3）分类决策存在错误率。

 

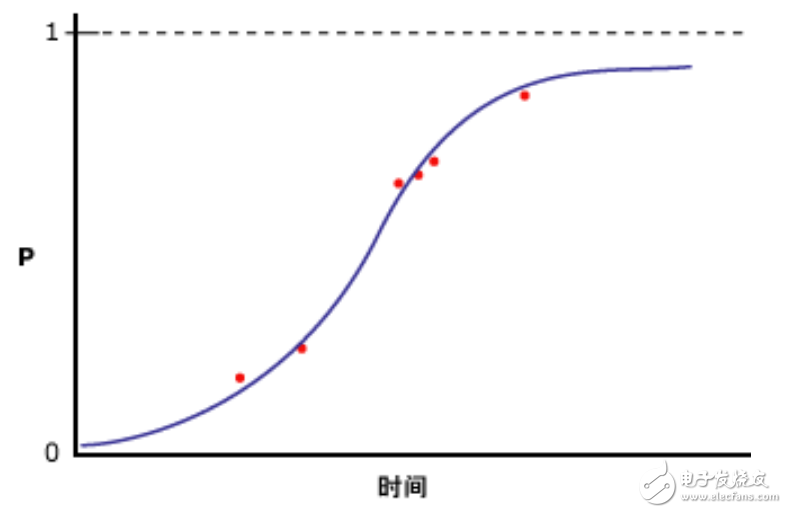
2.逻辑回归

优点：

1）实现简单，广泛地应用于工业问题上；

2）可以结合L2正则化解决多重共线性问题；

3）分类时计算量非常小，速度很快，存储资源低；

缺点：

1）不能很好地处理大量多类特征或变量；

2）容易欠拟合，一般准确度较低；

3）对于非线性特征，需要进行转换；

4）当特征空间很大时，逻辑回归的性能不是很好；

5）只能处理两分类问题（在该基础上衍生出来的softmax可以用于多分类），且必须线性可分。

 

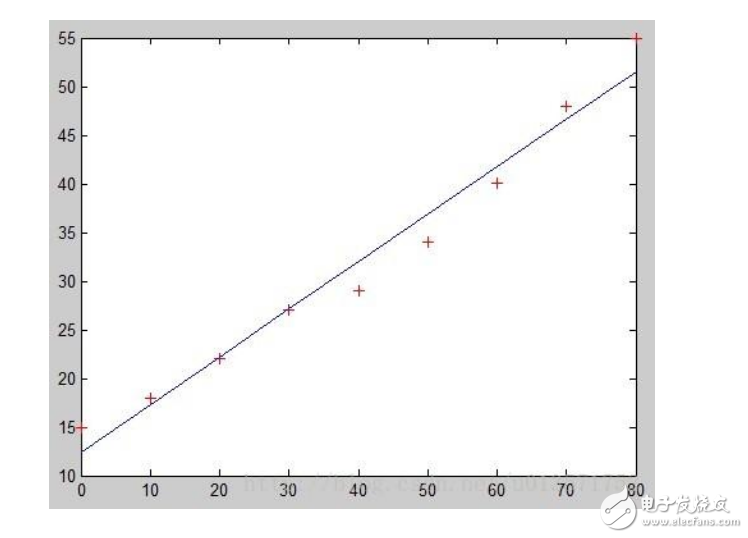
3.线性回归

线性回归与逻辑回归不同，它是用于回归的，而不是用于分类。其基本思想是用梯度下降法对最小二乘法形式的误差函数进行优化。

优点：实现简单，计算简单；

缺点：不能拟合非线性数据。

4.最近邻算法

优点：

1）对数据没有假设，准确度高；

2）可用于非线性分类；

3）训练时间复杂度为O（n）；

4）理论成熟，思想简单，既可以用来做分类也可以用来做回归。

缺点：

1）计算量大；

2）需要大量的内存；

3）样本不平衡问题（即有些类别的样本数量很多，而其它样本的数量很少）。

 

5.决策树

优点：

1）能够处理不相关的特征；

2）在相对短的时间内能够对大型数据源做出可行且效果良好的分析；

3）计算简单，易于理解，可解释性强；

4）比较适合处理有缺失属性的样本。

缺点：

1）忽略了数据之间的相关性；

2）容易发生过拟合（随机森林可以很大程度上减少过拟合）；

3）在决策树当中，对于各类别样本数量不一致的数据，信息增益的结果偏向于那些具有更多数值的特征。