

Matlab关于Apriori算法设计
电子常识
描述
1、Apriori算法实现步骤:
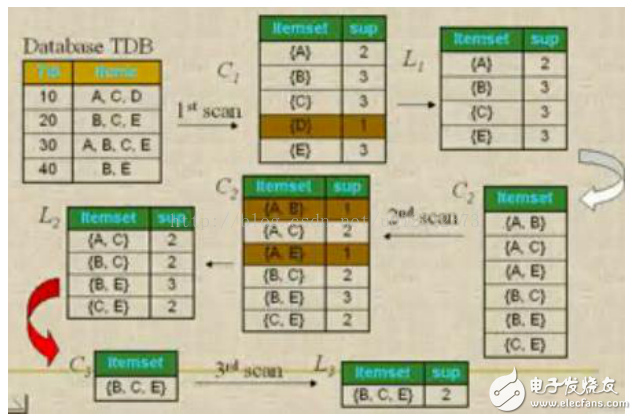
Apriori算法是一种最有影响的挖掘布尔关联规则频繁项集的算法Apriori使用一种称作逐层搜索的迭代方法,“K-1项集”用于搜索“K项集”。
首先,找出频繁“1项集”的集合,该集合记作L1。L1用于找频繁“2项集”的集合L2,而L2用于找L3。如此下去,直到不能找到“K项集”。找每个Lk都需要一次数据库扫描。
核心思想是:连接步和剪枝步。连接步是自连接,原则是保证前k-2项相同,并按照字典顺序连接。剪枝步,是使任一频繁项集的所有非空子集也必须是频繁的。反之,如果某
个候选的非空子集不是频繁的,那么该候选肯定不是频繁的,从而可以将其从CK中删除。
简单的讲,1、发现频繁项集,过程为(1)扫描(2)计数(3)比较(4)产生频繁项集(5)连接、剪枝,产生候选项集 重复步骤(1)~(5)直到不能发现更大的频集
2、产生关联规则,过程为:根据前面提到的置信度的定义,关联规则的产生如下:
(1)对于每个频繁项集L,产生L的所有非空子集;
(2)对于L的每个非空子集S,如果
P(L)/P(S)≧min_conf
则输出规则“SàL-S”
注:L-S表示在项集L中除去S子集的项集
例子:
代码实现:
在讲究代码之前,我先跟大家讲清楚我代码里面说需要的关键点。我的算法全部加起来最多一百多行代码,同时我包装在三个函数中:compute_sup.m(算支持度)、compute_conf.m(算可信度)、Apriori.m(主函数)。
-----------------------compute_sup.m-------------------------------------------------------------------------
function sup=compute_sup(S, D)
%------------S指传入的一个行向量--------
%------------D指整个数据集------------
sup=0;
[m,n]=size(D);
for i=1:1:m
%对应取出D的第i行与S对比,若D(i)-S所有的都>=0则支持度+1
if all((D(i,:)-S)>=0)
sup=sup+1;
end
end
-----------------------------测试------------------------------
已知(自己构造)
D =
1 1 0 0 1
0 1 0 1 0
0 1 1 0 0
1 1 0 1 0
1 0 1 0 0
0 1 1 0 0
1 0 1 0 0
1 1 1 0 1
1 1 1 0 0
输入:sup=compute_sup([1,1,0,0,0], D)
输出:sup = 4
--------------------------------------compute_conf.m-----------------------------------------------
function conf=compute_conf(Q,D)
%Q指传入的一条关联规则,如:[-1,0,0,1,0]指A->D=P(AD)/P(A)
s=abs(Q);
d=(abs(Q)-Q)/2;
conf=compute_sup(s,D)/compute_sup(d,D); %P(AD)/P(A)
------------------------------------------测试-----------------------------------------------------------------------------------
已知D
输入:conf=compute_conf([-1,0,0,1,0],D)
输出:conf = 0.1667 %置信度为0.1667
----------------------------------------------Apriori.m(算法的核心)---------------------------------
function [R,sup,conf]=Apriori(D,min_sup,min_conf)
%--------------R指生成的强关联规则----------------------
%--------------输出sup指支持度、min_sup-最小支持度-------------------------
%--------------
[n,m]=size(D);
min_sup=min_sup*n;
L=[];
%产生频繁集
C1=eye(m);
Ck=C1;
for k=1:m
Lk=[];
q=size(Ck,1);
for i=1:q
%-----------------剪枝-------------------------
sup= compute_sup(Ck(i,:),D);
if sup>=(min_sup)
Lk=[Lk;Ck(i,:)];
end
end
Ck=[];
q=size(Lk,1);
for i=1:q
for j=i+1:q
indi=find(Lk(i,:)==1);
indj=find(Lk(j,:)==1);
ind=indi-indj;
%从候选集中选出频繁集,相邻两个行对比,前k-1个相同,第k个不同,然后加入Ck。
if(all(ind(1:k-1)==0)&& ind(k)~=0)
Ck=[Ck;Lk(i,:)|Lk(j,:)];
end
end
end
L=[L;Lk];
end
%-------产生强关联规则-----------------
q=size(L,1);
R=[];
H=[];
M=[];
for i=1:q
ind =find(L(i,:)==1);
if length(ind)==1 continue;end
for j=1:length(ind)-1
SubSet= nchoosek(ind,j);
n=size(SubSet,1);
for m=1:n
L(i,SubSet(m,:))=-1;
H=[H;L(i,:)];
L=abs(L);
end
end
end
%---------------生成规则---------------
m=size(H,1);
M=abs(H);
T=[];
for n=1:m
sup=compute_sup(M(n,:),D);
conf=compute_conf(H(n,:),D);
if conf>=min_conf
T=[T;H(n,:),sup,conf];
end
end
R=[R;T];
end
---------------------------------------------------结果测试---------------------------------------------------------------------
已知
D =
1 1 0 0 1
0 1 0 1 0
0 1 1 0 0
1 1 0 1 0
1 0 1 0 0
0 1 1 0 0
1 0 1 0 0
1 1 1 0 1
1 1 1 0 0
min_conf = 0.6000
min_sup=0.2000
输入:[R,sup,conf]=Apriori(D,min_sup,min_conf)
输出:
R =
-1.0000 1.0000 0 0 0 4.0000 0.6667 %A->B
-1.0000 0 1.0000 0 0 4.0000 0.6667
1.0000 0 -1.0000 0 0 4.0000 0.6667
1.0000 0 0 0 -1.0000 2.0000 1.0000
0 1.0000 -1.0000 0 0 4.0000 0.6667
0 1.0000 0 -1.0000 0 2.0000 1.0000
0 1.0000 0 0 -1.0000 2.0000 1.0000
1.0000 1.0000 0 0 -1.0000 2.0000 1.0000
-1.0000 1.0000 0 0 -1.0000 2.0000 1.0000
1.0000 -1.0000 0 0 -1.0000 2.0000 1.0000
由于最小可信度是double型,所以弄得整个矩阵都是double行,有点失策。。。
-
Python的Apriori算法和FP-Growth算法是什么2020-06-04 1572
-
从五个方面让你了解人工智能算法中的Apriori2018-07-05 2663
-
数据挖掘Apriori算法报告2018-02-04 5390
-
Apriori算法详解2018-02-02 21733
-
简介Apriori算法并解析该算法的具体策略和步骤,给出Python实现代码2018-01-31 6310
-
基于Apriori算法的图书信息管理系统_梁子乐2017-03-19 921
-
基于Apriori_Pro算法的辅助知识获取技术研究2015-12-21 857
-
数据挖掘Apriori算法的改进2013-08-19 1114
-
关联规则Apriori算法的改进2011-05-13 936
-
一种新的改进Apriori算法2010-10-21 818
-
基于关联规则的Apriori-Partition算法的可视化2010-01-15 1031
-
一种新的改进的Apriori算法2009-12-25 1056
-
Apriori算法的一种优化方法2009-04-10 1060
全部0条评论

快来发表一下你的评论吧 !

