深度剖析比特币背后的技术细节

"拥有"一枚比特币究竟意味着什么？

很多人都听说过比特币, 它是一种数字货币，并不需要特定政府发行, 也不依赖银行来管理账户及验证交易, 甚至都没有人真正知晓其发明者，很多人都不知道上面那个问题的答案, 或者说至少不全了解. 要想搞明白，同时也为了让比特币背后的技术细节显得直观, 我们将从你会如何发明自的比特币的过程中一步一步地阐明.

首先我们从你用于记录你与好友们交易的公共账本开始, 然而你与好友及世界上的其他人的互信开始逐渐降低. 但聪明的你引入了密码学中的某些概念来解决信任危机, 你就创造了一种新事物，叫做"加密货币".

比特币只是第一个被广泛应用的加密货币的例子, 而如今有了更多其他的加密货币并与传统货币可以发生交易. 现在从你想要发明你自己的加密货币入手, 能帮助我们理解如今几大主流加密货币的理论基础, 了解其背后在不同方面存在着不同的设计空间.

事实上我选这个选题是因为在过去一年中针对加密货币有大量的关注、资本投入甚至老实讲还有媒体过分渲染. 我并不会对当前及未来的汇率发表评论及预测, 但我想任何想要购买加密货币的人都应搞明白加密货币究竟是怎么一回事.

我不会含糊地将其与挖矿作类比, 我会直接描述当我们发送、接受、创造加密货币时候, 计算机内部所发生的事情和原理.

我还要强调一点：虽然我们将花一些时间稍深入地了解背后的原理, 但是如果仅仅日常使用的话，我们并不需要了解其详细技术原理, 就像你不需要了解你刷信用卡背后所发生的一切一样. 与电子支付一样，加密货币也有很多方便易用的App可以直接用于发送和接受货币, 而不需要知道是怎么实现的.

区别在于加密货币的背后并不是某家银行来验证交易, 而是一套基于密码学中某些数学方法的, 来在去中心化的、互不信任的交易下验证交易的可靠.

在开始讲之前，你暂时把加密货币放在一边, 我们先从更基本的概念入手：账本和电子签名。

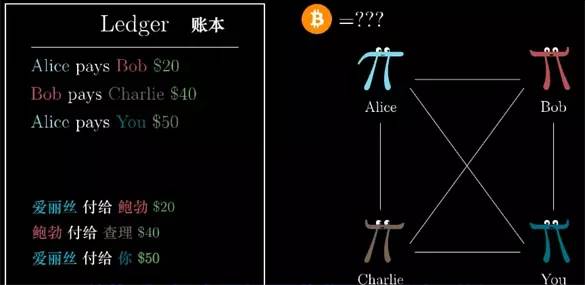
如果你和你的朋友们有很频繁的金钱来往, 比如AA支付晚餐的账单等等, 总是用现金总是不方便的. 所以可能会用到一个公共账本: 它记录了未来将要偿还的所有数目, 如Alice支付Bob 20元，Bob支付Charlie 40元等等.

这个账本必须是公开的，每个人都能查阅, 就像一个网站一样，每个人都能查阅并添加新的交易记录. 而到了每个月底大家对交易记录都无异议就会一起把账算清. 如果你入不敷出，就要再掏钱出来. 如果仍有结余，就可以从中拿回自己多付的钱.

所以这个简单体系的设计大概会是如下所述: 每个人都能向账本添加新的交易信息，到月底再用真金白银统一结算.

但这样的公共账本存在一个问题，正因为每个人都能添加交易记录, 应该怎样避免Bob在没有经过Alice同意的情况下偷偷记下：Alice给Bob 100元. (这样月底结算时候, Alice就要为这笔捏造出来的交易付钱出来了).

我们又凭什么相信账本中的记录都准确无误呢, 这里就需要密码学中的电子签名技术. 就像手写签名一样，Alice需能在每笔交易信息边上留下记录, 以证明她了解并且认可这笔交易发生, 而且这个签名不能被他人获取并伪造.

电子签名确保交易的真实性

乍一思索电子签名似乎不太可能实现, 无论电子签名是如何存储的，计算机都可以读取并复制. 那究竟该如何防止伪造呢? 要实现电子签名，每个人都需要生成一对秘钥: 公共密钥及私人密钥.

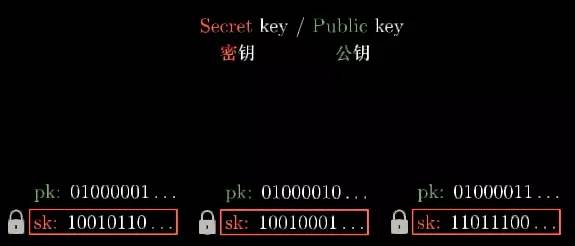
每一个密钥其实都是一串 0 或 1 比特串. 私人密钥有时也被叫做"秘密"钥匙, 以便能够缩写成 sk, 公共密钥则缩写成 pk.

正如其名，私人密钥是由你自己保存的, 现实生活中，你本人所签署的所有文件中的签名都是一样的. 电子签名则更进一步，它会随着签署的内容变化而改变. 它看上去就是一串10代码，通常长度是256位. 而任何要加密内容的一个字符的变动都会让这串产生的新的签名变得完全不同.

正式一点地讲，产生这样的签名需要一个函数 Sign, 它同时要求所签署的内容以及你的私人密钥, 也就是 Sign(签署的内容, 秘钥) → 生成新的签名 .

私人密钥确保了只有你本人能产生这个电子签名, 这个产生的签名还取决于所要签署的内容, 就意味着其他人不能简单地复制这个签名, 并在其他捏造的内容上伪造另一个签名(因为捏造的内容肯定与原内容不同).

与此同时还有一个函数 Verify 验证用于验证签名是否真实, 而这个函数还需要三样东西: 签署的内容, 生成的签名, 公共密钥. 它的作用是告诉我们这个签名是否是由输入公钥对应私钥来生成的.

这里并不会具体讨论这些函数具体如何实现([遇见数学]会在未来《图解密码学》中介绍), 但它保证了如果你不知道对方私钥的情况下，几乎不可能找到一个正确的签名. 准确地讲，只有通过穷举并反复验证才有可能找到正确的签名, 然后用公开的公钥 pk 来通过验证.

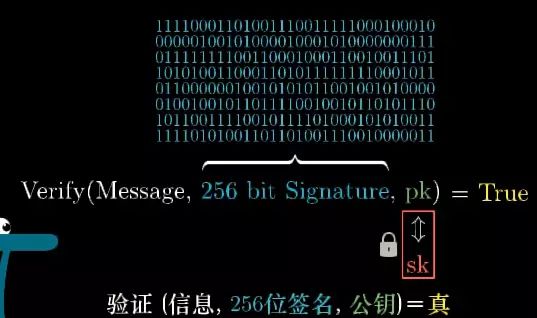
现在想想256位比特到底有多少可能的签名, 总共有 2256 次方个可能的签名, 这是一个天文数字, 称其为天文数字实际上又远远高估了天文学的范畴, 我还做了另一个补充视频来演示这个数字究竟有多大，文后会详细介绍。

现在如果一旦你验证了一个签名是真的, 你就能相当有把握地认为, 这个签名只能由他本人持有的私钥加密产生.

编号确保交易唯一性

现在确保了每个人都会在交易信息后面签名, 不过仍然会存在另一个问题, 比如Alice签署了一条Alice支付Bob 100元的交易记录, 即便Bob不能在Alice的新交易记录上伪造签名, 他还可以把这条记录随心所欲地复制好几遍, 因为这些记录以及它对应的签名都是正确的.

要解决这个问题，你在签署每一笔新的交易信息时, 交易信息还必须包含一个唯一的编号与之对应. 那样如果Alice多次支付Bob 100元的话, 账本上的每条记录都会要求一个新的签名.

有了电子签名就解决绝大部分了原本体系中的信任危机, 但要真正实现，仍然需要依赖一个类似的信用机构, 也就是说你信任每个人到了月底都会出现并用现金结算, 因为万一Charlie欠了很多钱但就是不出来还钱该怎么办, 这就是月底人们再次用现金结算的唯一原因 - 担心某些人(比如 Charlie) 欠了很多钱.

聪明的你想到了一个方法就不需要真正再用现金结算, 只要能够避免其中有些人的支出金额小于剩余可支付金额. 比如所有人刚开始就需要往账上支付100元，账本上最先记录几条：Alice获得100元，Bob获得100元，Charlie等等.

现在只需要拒绝在账本上记录某些人入不敷出的交易就可以了, 举个例子，如果前两条交易记录是: Charlie支付Alice 50元，Charlie支付Bob 50元. 再来如果Charlie还要支付你20元的时候，那这项交易将是无效的，这就跟他没有签名一样是无效的. 

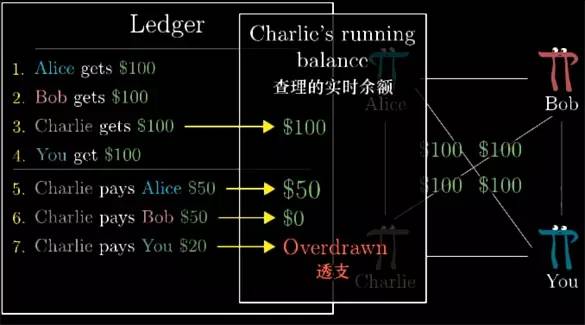
不过这就意味着验证当前的一条交易, 就需要了解截至当前所有的历史交易信息. 这在加密货币中同样如此，并且仍有待优化的余地.

但有趣的是，这个设计真正去掉了账本和真实美元之间的联系, 理论上如果世界上所有人都是用这个账本, 你整个一生都可以在这个账本上支付并获得收入中度过, 根本没有必要获得真实的货币.

为了强调这一点，我们把账本上的货币单位称之为"账本元"，并简称为LD. 当然, 你也可以随时将LD自由地兑换成真的美元.

举个例子，Alice在现实中给了Bob 100元, 同时Bob在公共账本上记上Bob支付Alice 100元. 但这样的兑换并不在这套系统的设计初衷之内, 所以不会受协议的保护. 这样的兑换与美元和欧元或市场上其他的货币兑换类似, 那是另外一个事情了.

比特币的核心

这是理解比特币和其他加密货币的最重要的信息了, 它实际上就是一个账本, 所有的历史交易就视为货币的实体.

当然就比特币而言, 人们只有用现金购买和使用比特币才会在账本上记录. 但新的比特币如何产生我一会儿再细说.

但此之前，我们的LD体系和实际的加密货币还有一处不同, 我刚提到这个公共账本存在于某个公共地点. 比如一个网站，所有人都能登陆并添加记录, 那样的话我们就必须信任这一中心机构. 那究竟谁来管理这个网站，谁来控制添加记录的规则呢?

考虑到如果让所有人都能获取这份账本也就不需要信任中心机构了. 当你需要发生交易，如Alice支付Bob 100元, 你需要将这个信息广播给网络中所有的其他人, 他人收到了这个信息都在自己那份账本上记下这条交易.

这样想法虽然简单，但真的这样设计就会相当糟糕, 因为如何确保所有人手里都是正确的那份账本呢

当Bob收到了如Alice支付Bob 10 LD 的交易，他如何确保并相信其他所有人也同样收到了这一信息, 以便未来能让他在可以用这 10 LD支付给Charlie做交易呢?

试着想想是你自己收听着来自外界的交易信息广播, 该如何确保其他人和你一样以相同的顺序接受交易信息, 这才是关键所在，也是一个有趣的难题.

你能想出一个协议来决定接受或拒绝收到的交易信息, 而且你确信其他所有人在这个方法下能以同样的顺序接受交易信息, 最终可以形成一模一样的账单, 这也是比特币原始论文中详述的部分.

简单地讲，比特币给出解决办法是: 选择信任消耗最多计算资源(计算量最大)的那份账本. 我会花一些时间详细讲是什么意思, 它涉及到"加密散列函数"这个概念.

基本的思路如下：如果你将计算资源的消耗作为你信任的基础，那么伪造交易记录和账本不一致的情形所要耗费的计算力成本要高到不可行。

这个想法实在是太酷了！如果你懂了，你就会理解比特币和其他加密货币的核心.

那么首先，什么是散列(哈希)函数？这些函数的输入可以是任何信息或文件, 它们会输出一个固定长度的比特字符串，如256位, 这个输出值叫做这个信息的散列值，或者称其为"摘要", 它故意设计成会输出看似相当随机的内容, 但并不是随机的，只要是给定相同的信息总是输出相同的内容.

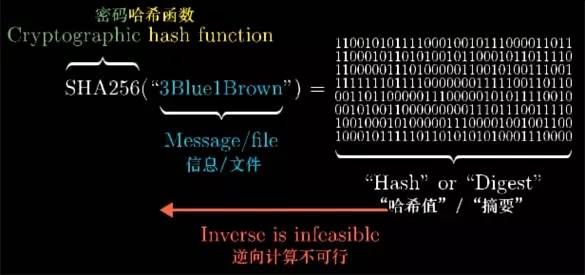
但如果你将输入稍作修改，也许仅仅只是修改了其中一个字符，最终的散列值会变得面目全非. 事实上，我这里做演示的散列函数叫做"SHA256" .

输入的轻微修改，输出就会完全不同，毫无规律可言, 明白了吧，这不是普通的散列函数，这是加密散列函数, 这就意味着逆向计算是不可能的.

如果告诉你一串 256 位的1,0的字符串然后问你, 找到SHA256 函数输入的内容, 使得两者经过 SHA256 后具有同样的结果. 你只有一个一个暴力去试错的方法.

不过你想感受一下 2^256 次方个尝试究竟需要计算多久, 可以看看这个补充视频(《256位加密有多安全?》过几天[遇见数学]会整理出来).

你会想如果知道了这个函数的运作细节, 是不是就可以不用瞎猜, 而是可以倒推回来猜出这个输入呢. 但目前没有人可以做到.

有趣的是，目前还没有严格的证明逆向计算是困难的, 但目前大量的安全行业和加密需求都取决于加密散列函数以及它的这个性质.

如果你细看浏览器和 youtube 建立的加密连接背后的加密算法, 或浏览器连接银行网站时, 你很可能会看到SHA256算法.

但现在，我们的关注点会是这样的散裂函数如何证明账单上一系列的交易是和一个很大计算量有关系呢?

想想如果有人给你一份交易记录，并说"嘿！我发现了一个特殊的数字(下图中账本中绿色数字 1073765433)，你把这个数字放在这份交易记录后面, 然后在给整个交易记录信息进行SHA256函数计算后, 前面30个数字都会是0！"

你想想找到这样的一个数字有多难？对于一个随机的信息，其散列值前30位都是0的概率是2的30次方分之一, 也就是差不多是十亿分之一, 而且因为SHA256是一个加密散列函数, 找到这个特殊数字的唯一方法只能是暴力穷举验证, 所以你基本上已经尝试了十亿次, 才找到了这个特别数字.

而你一旦知道了这个数字，很快计算一下这个交易列表和数字在一起作为输入, 经过散列计算后发现开头确实是30个0就行列.

换言之，你能很快地验证他们确实经过了大量的计算, 而你不需要亲自消耗这么大计算量。这叫做"工作量证明".

重要的是，这个工作量证明本身就对应列这份交易记录. 如果你更改了其中一条交易信息，即便是修改列一个数字, 也会完全改变最终的散列值. 所以就又需要经过十亿次尝试才能找到新的工作量证明 - 即找到那个特别数字, 接在你修改后的交易列表后面, 使得对应的散列值开头是 30 个0.

现在回过头来考虑我们的分布式账本的情形：每个人都在广播交易信息，我们想找到一个方法能让所有人都认可一份正确的账单. 我前面说过比特币原始论文的核心点就是, 每个人都信任需要消耗最大计算量的那份账单.

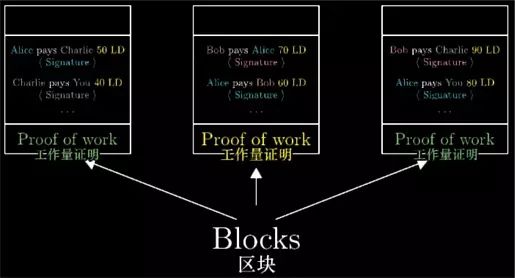
要实现这个想法首先需要将账单整理成"区块". 这些区块包含了一系列交易信息以及其工作量证明, 也即有一个特别数字满足其散列值以一系列0开头.

我们暂时先定60个0开头吧，一会儿我们会回头来看如何系统地确定这些0的个数.

类比于交易信息要经过发送方签名才被认定为有效, 同样的, 一个区块只有当它有工作量证明时才被认定为有效.

而且为了确保这些区块有一个标准的顺序, 我们规定前一区块的散列值必须加入到当前区块的头部信息中.

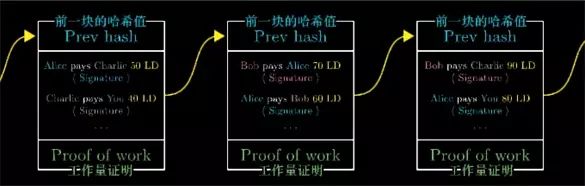
这样的话，如果你回头想改变其中某个区块的内容, 或交换两个区块的顺序, 你就会改变它后一个区块的内容, 也就改变了那个区块的散列值, 然后又影响到再下一个区块......

这就需要重新计算所有这些区块的散列值，重新寻找每个特别数字使得区块的散列值以60个0开头. 因为所有的区块以这种方式相互链接, 所以我们一般不把它叫做账本，而是为"区块链"(blockchain).

在这个新的体系之下，我们现在允许世界上的每个人都参与建造区块, 意思是说他们都可以收听网络中的交易信息，整理这些信息生成区块，然后花大量的计算工作, 找到那个特别数字使得区块的散列值以60个0开头.

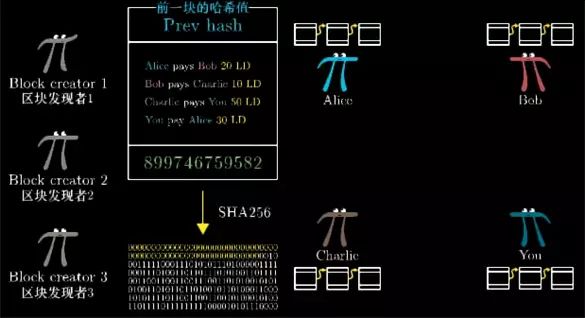
一旦找到了这个数字，他们就将这个区块广播出去. 为了奖励这个区块建立者所消耗巨大的计算量付出，当她建立了一个区块，我们规定她可以把一笔特别的交易信息放在账单开头，即：让她凭空获得10 LD。这叫做"区块奖励"，这并不属于任何交易, 它并不来自于其他人，所以也并不需要签名。

这也意味着, 每一个新建的区块都会增添新的虚拟货币, 建立区块通常叫做"挖矿"，因为它会需要消耗大量的计算工作量, 挖矿会为整个经济中引入新的货币量.

所以当你听到或看到矿工时, 你现在明白他们所做的其实就是:收听交易信息，建立区块，广播区块，并获得新货币的奖励，如此而已．

而在矿工眼中，每个区块就像是一个小型的彩票，每个人都想尽可能快得猜对那个特殊的数字，直到其中有一个幸运儿找到了那个特别数字，能让区块的散列值以很多0开头，然后他们就得到奖励.

而对于其他只是想利用这个系统做交易的人而言，并不需要收听交易记录，他们只需要收听被矿工广播的区块即可，然后更新自己保持的区块链就可以了.

现在我们协议的关键点来了, 如果我们收到了两份完全不同的区块链，其中交易信息相冲突的时候, 你只保留最长的那一个，也就是包含最大的工作量的那一份(比如区块链长度为 4和5 , 就选择长度为 5 的那份)。

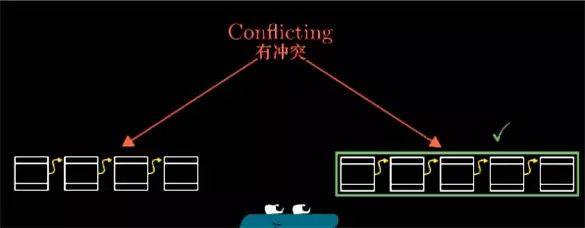
如果暂时难分上下，等待下一个区块的广播，总有一个会形成更长的区块链, 所以即便没有中心权威机构，所有人也都各自记录自己的那份区块链, 但如果每个人都信任最多工作量的那个区块链，我们就达到了一个去中心化的共识.

为了理解这个系统为什么可信，以及怎样才应该相信每一笔交易是否真实. 我们其实可以去理解, 要怎么做才能在这个系统下进行欺骗.

也许Alice想要用一个伪造的区块欺骗Bob, 也就是她给Bob一个区块里包含里她支付Bob 100账元的信息, 但她没有把这个区块广播给网络中的其他人. 那样的话，其他人都还以为她仍然持有那100账元. 为了做到这一点, 她要比其他所有矿工先找到工作量证明才能欺骗所有人, 因为所有的矿工他们也都在独立建造区块.

而这确实是有可能发生的！有可能Alice刚好比其他所有人都先找到了这个表示计算量的特殊数字, 但Bob也还会收到来自其他矿工的区块广播. 所以为了让他相信她那份伪造的区块，Alice后面都要持续重新计算, 她那份伪造给Bob的区块后面的所有区块, 这些区块和Bob收到了来自其他矿工的区块都不同.

但系统协议规定Bob总是信任他所指的最长的那一个区块链, Alice在前几个区块还有可能保持领先 - 刚好碰巧她比其他所有矿工都先找到那个区块.

但除非她拥有接近所有矿工的计算资源的50%, 否则, 从概率上看, 基本能肯定的是其他所有矿工计算的区块会比Alice伪造给Bob的区块形成的区块链更长更快.

所以经过足够长的时间，Bob会拒绝他收到的来自Alice的区块链, 而选择其他所有人都在使用的最长的区块链.

注意了, 这意味着你不一定要信任你刚刚接受到的新区块, 而应该等后面有新的几个区块添加后, 如果你还没收听到更长的区块链，你就能信任这个区块的确属于其他所有人都在用的那条链上.

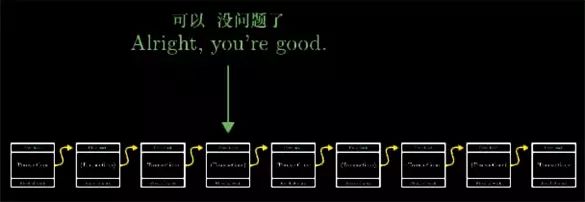
到此，我们讲解了所有主要内容, 这个基于工作量证明的分布式账本系统, 基本上就是比特币还有其他加密货币的工作原理. 再讲讲更多的细节, 刚我讲到工作量证明, 就是寻找那一个特别数字, 满足其区块的散列值以60个0开头. 而现实的比特币协议中会定理改变 0 的个数, 好保证平均每10分钟可以产生一个新的区块.

当有越来越多的矿工加入到"挖矿"的行列中后, 这个计算的挑战性也越来越高. 好让这个小彩票, 大约每 10 分钟才能有一个人中奖. 很多新的加密货币有更短的区块时间间隔.

比特币体系中所有的比特币都来自于生成新区块的奖励, 在一开始，是每区块50个比特币. 还有一个叫做"Block Explorer"的网站你可以去看看, 上面能轻松地看到比特币区块链中的信息, 如果你看区块链最初识的那几个区块, 它们除了奖励给矿工的50个比特币之外并没有其他交易.

但每过210000个区块，差不多每4年，区块奖励就会减半. 现在，每个区块的奖励是12.5个比特币, 也因为这个奖励随着时间等比减少, 也就意味着最终可获取的比特币不会超过21000000. 但这并不是说矿工最终赚不到钱, 除了区块奖励外，矿工还可以获得交易费, 每当你支付时，你可选择一小笔交易费一起支付, 这笔交易费最终会给包含这笔记录的区块建立者, 你这么做能够激励矿工们继续工作, 将包含你这笔交易信息的区块广播给网络中的其他人.

在比特币中，每个区块包含约2400笔交易记录, 很多批判家认为这个限制过于严格, 与VISA比较，VISA每秒平均处理约1700笔交易, 而有能力每秒能够处理多达24000笔交易. 相比而言比特币较慢的交易速度使得它的交易费用更高, 正是交易费用决定了矿工哪些交易加入到新的区块中.

除了以上这些加密货币的基础知识, 还有其他许多不同的加密货币的系统设计尚未涉及, 但我希望这个视频能称为坚实的求知欲基石, 感兴趣的话, 可以扩展阅读, 继续学习. 正如我开头所说，我做此视频的初衷是因为许多的资金涌入加密货币中, 是好是坏我并不过多评价, 但我认为想要进入这一领域的人, 至少了解这门技术的基础, 应该是很有益的.

256加密有多安全

为了攻破一个安全系统, 你必须得猜对一个256位的比特串. 第一次是在电子签名的部分提的, 第二次是在密码散列函数的部分提到的.

比如说，假如你想找到一条信息让它的SHA256 散列值(哈希值)等于某个 256位比特串的话, 没有其他办法，只能暴力猜测, 并检验结果. 这需要尝试 

22562256 次.

这个数字比我们通常遇到的数都要大得多, 因此很难去体会它的规模. 不过我们不妨试一试, 22562256 也就是 232232 , 和它自己相乘 8 次 

这样分解的好处在于我们知道 232232 大约是 40亿这样一个数量. 

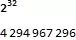
我们起码可以想象"小一点"这个数字吧, 嗯，再来就是去体会 40 亿连续相乘 8 次是怎样的概念？很多人知道，我们的电脑里的 GPU 可以飞速的进行大量的并行计算. 因此要请你专门让 GPU 反复计算密码散列函数. 一个性能很好的 GPU 每秒也许能算出接近 10 亿个散列值.

假如你拿上一堆这样的 GPU , 而让你这台超级电脑每秒能算 40 亿个散列值, 那么就开始的 40 亿代表了你这台超级电脑每秒算出的散列值的数目.

想象一下 40 亿台这样满载 GPU 的超级电脑, 跟 Google 对比下, 虽然谷歌没有对外公布他们的服务器数量, 但是有估计说大概有几百万台. 现实中他们大部分服务器的算力都不如我们满载 GPU 的电脑强, 我们假设谷歌把上百万个服务器全换成这样的超级电脑. 那么 40 亿台超级电脑大概是 1000 个这种打了鸡血后的谷歌. 我们就把这个算力叫做 "千谷歌"吧.

我们再往右看, 全世界的人口大概有73亿, 接下来我们假设一多半的人(40亿台)都拥有自己的千谷歌,

然后想象, 40 亿个这样的地球, 作为对比，银河系大约有 1000 到 4000 亿颗恒星, 虽然我们并不确定，但估算大致就在这个范围. 所以这相当于银河系的 1% 恒星, 并且每个地球上一半的人口都拥有自己的千谷歌.

接着想象, 40 亿个这样的银河系, 我们把它叫做"亿万星系超级计算机", 每秒能猜 21602160 次.

40 亿秒, 大概是 126.8 年, 它的 40 亿倍, 就是 5070 亿年, 差不多是宇宙年龄的37倍. 所以就算你有( GPU 满满的超级计算机) * (地球上超过一般人都拥有千谷歌) * (行星云集) * (亿万星系计算机) * (猜上 37 倍宇宙年龄的时间), 也只有 40 亿分之一的可能性猜测到正确的数字.

密码学原理

知道什么是公钥密码学的人可能已经听说过ECC、ECDH或是ECDSA。第一个术语是椭圆曲线密码学（Elliptic Curve Cryptography） 的缩写，后两个是基于它的算法名称。

如今，我们可以在TLS、PGP和SSH中见到椭圆曲线加密系统，这是现代网络和IT世界所依赖的三种主要技术。比特币和其他加密货币就是利用这种加密算法进行加密的。

在ECC流行起来之前，几乎所有的公钥算法都是基于RSA、DSA和DH ———— 基于模运算的可选加密系统。RSA及其友类算法在当前仍非常重要，经常与ECC一并使用。不过，RSA及其友类算法背后的原理很容易解释，因而被广泛理解，一些简单的实现也可以很容易编写出来；但ECC的实现基础对于大多数人来说仍很神秘。

通过一系列的博文，我打算用一个通俗的方式介绍椭圆曲线密码学。我的目标不是提供ECC完整和详细的指导（网上有这方面的充足信息），而是简单概述“ECC是什么、为什么它被认为是安全的”，避免把时间浪费在长篇的数学证明和恼人的实现细节上。我还将提供一些辅助示例以及可视化图形工具和脚本给大家使用。

具体来说，我将触及以下主题：

1. 基于实数域的椭圆曲线和群公理（本文中涉及）

2. 基于有限域的椭圆曲线和离散对数问题

3. 密钥对的生成以及两个ECC算法：ECDH和ECDSA

4. 破坏ECC安全性的算法，并与RSA作对比

为了能够理解本文所述的内容，你需要了解集（set)理论、几何、模运算等基本概念，并大致知道对称式和非对称式加密。此外，你需要清楚的知道什么是“易解”问题，什么是“难解”问题，以及它们在密码学中的角色。

准备好了吗？开始！

椭圆曲线

首先，什么是椭圆曲线？ MathWorld 线上数学百科全书给出了一个极好并完整的定义。不过，针对我们的学习目的，椭圆曲线将简化为用下面这个等式所描述的点的集合：

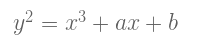
其中， 4a3 + 27b2 ≠ 0 (这是为了排除奇曲线)。上面的等式称为椭圆曲线的魏尔斯特拉斯范式（ Weierstrass normal form）

不同的椭圆曲线的不同形状 (b = 1, a 取值由 2 变化至 -3).

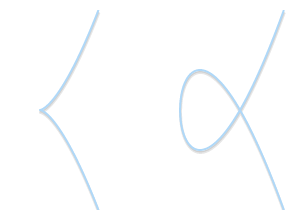
奇点类型: 左侧, 带一个尖角的曲线 (y2 = x3)。右侧, 带一个自交叉的曲线 (y2 = x3 – 3x + 2). 这两种都不是有效的椭圆曲线。

根据a和b的值，椭圆曲线在平面上可以呈现不同形状。可以很容易看出并验证： 椭圆曲线是关于x-轴对称的。为了实现我们的目标，我们还需要把一个无穷远点（亦称之为理想点) 视为椭圆曲线的一部分。从现在开始，我们将用符号0（零）来代表无穷远点。

如果我们想显式地将无穷远点纳入考虑，我们可以按如下的方式细化椭圆曲线的定义：

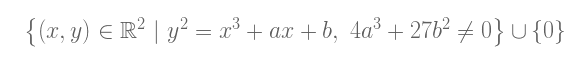
群

数学中的“群”是一个由我们定义了一种二元运算的集合，二元运算我们称之为“加法”，并用符号“+”来表示。为了让一个集合G成为群，必须定义加法运算并使之具有以下四个特性：

1. 封闭性：如果a和b是集合G中的元素，那么（a + b)也是集合G中的元素。

2. 结合律：(a + b) + c = a + (b + c);

3. 存在单位元0，使得a + 0 = 0 + a =a;

4. 每个元素都有逆元，即：对于任意a，存在b，使得a + b = 0.

如果我们增加第5个条件：

5. 交换律： a + b = b + a

那么，称这个群为阿贝尔（abelian)群。

配上通常概念的加法时，整数的集合Z就是一个群（同时还是个阿贝尔群）。而自然数的集合（N）就不是群，因为它不满足第4个特性。

“群”很有用，因为一旦我们证明它具备上述4个特性，那么我们就可以自由地获取到一些其他特性。比如：单位元是唯一的；此外，逆元也是唯一的，即：对于每一个a，存在唯一的一个b，使得a + b = 0 （我们可以将b写成-a）。后面我们会发现，群的这些特性以及其他存在的事实，或者直接或者间接，对于我们来说非常重要。

椭圆曲线的群公理

我们可以定义一个基于椭圆曲线的群。如下：

• 群中的元素是一条椭圆曲线上的点;

• 单位元为无穷远点O;

• 点P的逆元是其关于x-轴的对称点;

• 加法，满足以下规则: 对于3个处在同一直线上的非零点 P, Q 和 R, 它们的和 P + Q + R = 0.

同一直线上的三个点之和等于0.

注意一下最后一个规则，我们需要的只是三个点同线，与点的次序无关。这意味着，如果P、Q和R同线，那么P + (Q + R) = Q + (P + R) = R + (P + Q) = • • • = 0. 这样，我们直观地证明了我们的“+”运算既满足结合律也满足交换律：我们创建了一个阿贝尔群。

到目前还很不错。但我们如何实际计算任意两点之和呢？

几何加法

得益于我们使用的是一个阿贝尔群，我们可以把 P + Q + R = 0 写成P + Q = –R。方程的这一形式，让我们可以推导出计算两点P和Q之和的几何方法：画一条过P和Q点的直线，这条直线与曲线相交得到第3个点R（这一事实意味着P、Q、R必然共线）。如果我们获取了该点的逆元-R，那么我们就得到了P + Q的结果。

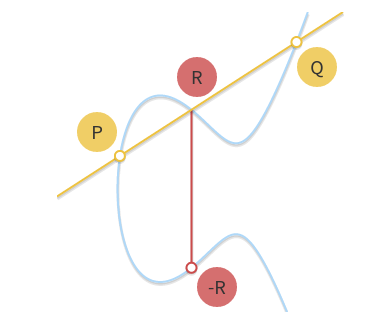
过P和Q画一条直线。该直线与曲线相交与第3点R。与之对称的点-R即为P+Q 的结果

这种几何方法可以成立，但还需一些改进。特别是，我们需要回答以下几个问题：

• 当P = 0或Q = 0时怎么办? 显然，我们无法画任何直线（0点不在xy-平面上）。不过，由于我们定义了0点为单位元，所以，对于任意P和任意Q，都有：P + 0 = P ， 0 + Q = Q

• 当P= –Q时怎么办? 这种情况下，通过两点的直线是一条垂线，与曲线不会有第三个交点。不过，由于P是Q的逆元，那么由逆元的定义可知P + Q = P + (-P) = 0 .

• 当P= Q时怎么办? 这种情况下，经过该点的直线有无数条。事情开始有点复杂了。不过，先想像一个点 Q’ ≠ P。如果我们令Q’ 向P逼近，越来越靠近P会怎么样？

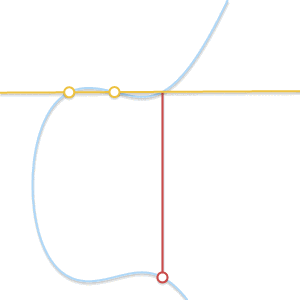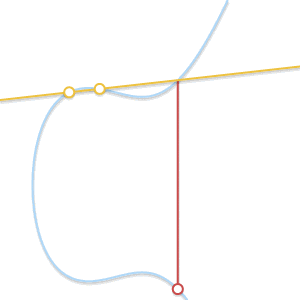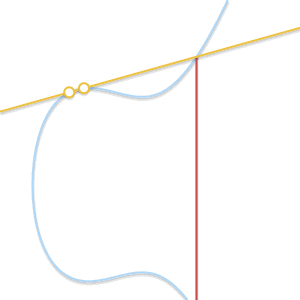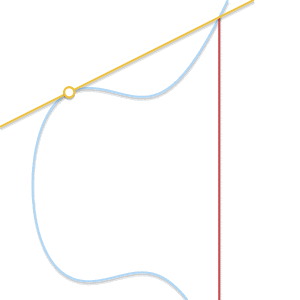
随着两个点越来越接近，过这两点的直线最终变成了曲线的切线

随着Q’ 趋向P, 过P和Q’ 的直线最终成为曲线的切线。看到这一点，我们可以定义 P + P = –R, 其中R是过P点的切线与曲线的交点。

• 当P ≠ Q，但找不到第三个点R时怎么办? 这种情况和上面那个非常类似。实际上，这是因为过P和Q的直线与曲线相切。

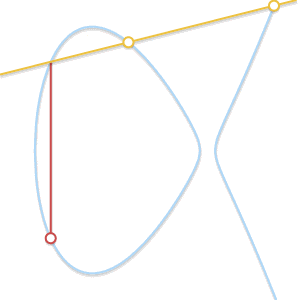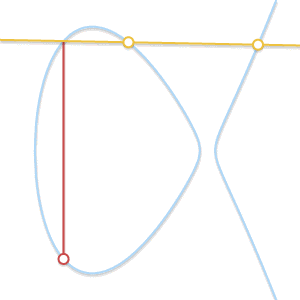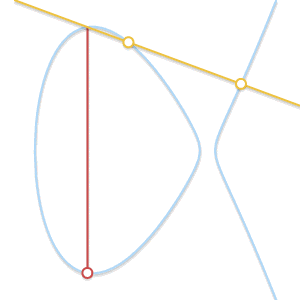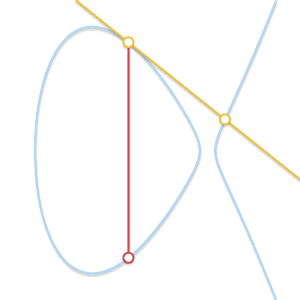
如果直线与曲线只有两个交点，那么该直线为曲线的切线。可以很容易地看出，两点相加的结果是其中一点的对称点

• 假设P是切点，在上一情况中，我们已经得出P + P = –Q. 等式现在变为 P + Q = –P。 如果Q 是切点，正确的等式应为 P + Q = –Q.

现在，用几何方法可以完全覆盖所有情况了。用一支铅笔和一把尺，我们可以做任意椭圆曲线上所有点的加法运算。如果你想试试，请到 HTML5/JavaScript visual tool 看一下，这是我建的一个工具，用来计算椭圆曲线的加法!

代数加法

如果我们想把点的加法运算计算机来完成，那么需要将几何方法转化为代数方法。将上面描述的规则转换为一组公式看似简单，实际上是非常繁琐的，因为需要求解三次方程。因此，这里我只通报结果。

首先，先抛开最恼人的极端情况。我们已经知道P + (-P) = 0, 还知道P + 0 = 0 + P = P。所以，在我们的公式中 ，我们将避免这两种情况，只考虑两个非零、非对称点 P = (xP, yP) 和Q = (xQ, yQ).

如果 P 和 Q 不相同， (xP ≠ xQ), 过这两点的直线斜率为:

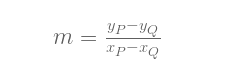
该直线与椭圆曲线交于第三点 R = (xR, yR):

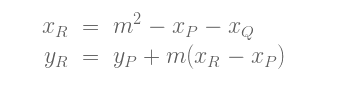
或是, 等价形式:

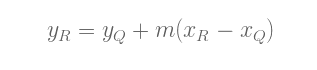
因此，(xP, yP) + (xQ, yQ) = (xR, –yR) (注意正负号，记住P + Q = –R).

如果我们想检查这一结果是否正确，我们将不得不检查R是否在曲线上，同时P、Q、Q是共线。检查点是否共线轻而易举，但检查R是否在曲线上就不容易了，因为需要求解三次方程，这可不是什么好玩的事儿。

不过，我们可以用一个例子来试一下：根据 可视化工具的计算， 当 P = (1, 2) 、Q = (3, 4) ，椭圆曲线 y2 = x3 – 7x + 10, 两点之和 P + Q = –R = (-3, 2). 让我们看一下与我们的公式是否一致:

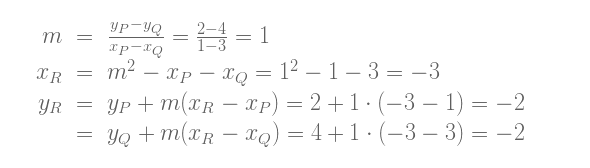
好的，正确!

注意上面的公式即使在其中一个点P或Q是切点的情况下也成立。让我们试一下P = (-1, 4) 、 Q = (1, 2).

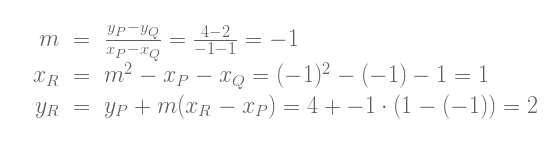
我们计算出 P + Q = (1, -2), 与使用 可视化工具计算出的结果相同。

P = Q 的情况需要做点不同的处理：方程中 xR 和 yR 相同, 由于 xP = xQ, 我们必须使用不同的公式来计算斜率：

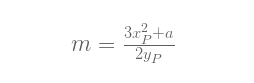
注意，我们可以料到，m的表达式实际是下面这个函数的一阶导数:

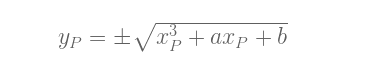
为了证明结果的有效性，只要检查R是否在曲线上，以及P和R在曲线上只有两个交点就足够了。但同样，我们不去证明这一事实，而是试算一个例子: P = Q = (1, 2).

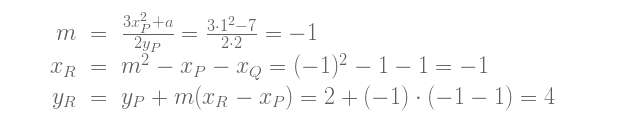
公式计算出 P + P = –R = (-1, -4).正确!

尽管推导过程真的是极其繁琐，不过最后的公式还是很简洁。这要感谢魏尔斯特拉斯范式：要是没有这一范式，最后的公式会真的又长又复杂。

标量乘法

在加法之外，我们还可以定义另一种运算：标量乘法，即：

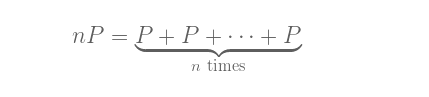
nP，其中n为自然数。我为标量乘法也写了个 可视化工具 ，如果你想试算时可以使用。

用这种形式表示时，计算nP似乎需要n次加法运算。如果n有k个二进制位，那么算法的时间复杂度将为O（2^k)，这真不是很好。不过存在一些更快的算法。

其中一种是“加倍（double)与相加（add)”算法。

计算的原理可以用一个例子来更好地解释。取n = 151。它的二进制表示形式为100101112 。这一二进制表示形式可以转换为一系列2的幂之和。

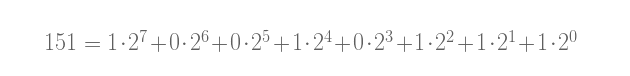
(取n的 每个二进制位上的数字，并用它乘以一个2的幂.)

用这种方法，我们可以将n这样写:

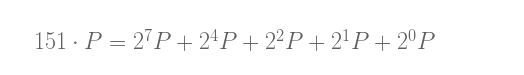
“加倍（double)与相加（add)”算法需要这样做:

• 取 P.

• 加倍，得到2P.

• 2P与P相加(为了得到 21P + 20P).

• 加倍 2P，得到22P.

• 与前一结果相加 (得到 22P + 21P + 20P).

• 加倍 22P，得到23P.

• 对23P不做任何操作.

• 加倍23P，得到24P.

• 与前一结果相加 (得到 24P + 22P + 21P + 20P).

• …

最后，我们可以计算151 • P ，只需7次“加倍”运算和4次“相加”运算。

如果还不够清楚，这里有一个实现该算法的python代码段：

如果“加倍”和“相加”操作复杂度均为O(1),那么 该算法的时间复杂度为O(log n) (或是O(k)，如果我们考虑的是二进制位的长度），这相当不错。比最初O(n)的算法肯定要好得多。

对数

给定n和P, 我们现在至少有一个多项式时间算法来计算Q = nP。不过，逆运算需要计算多少轮呢？如果已知Q和P，我们想求解n会怎么样？这一问题被称为对数问题。我们称之为“对数”而不是“除法”是为了与其他加密系统（在术语上）保持统一（那些系统中，不称“乘法”，而称“幂”）。

我不知道任何关于对数问题的“易解”算法，不过，通过摆弄乘法 ，很容易发现一些模式。例如，对于曲线 y2 = x3 – 3x + 1和点 P = (0, 1). 我们可以立即验证出, 如果n为奇数，nP在曲线的左半面，如果n为偶数，nP在曲线的右半面。如果我们尝试更多次，我们或许可以找出更多的模式，最终可以让我们写出一个算法来高效计算那条曲线的对数问题。

不过，对数问题有一个变体：离散对数问题。在下一篇博文中，我们将看到，当我们对椭圆曲线的域进行缩减后，标量乘法仍旧”易解“，而离散对数问题成为了”难解”问题。这种双重性是椭圆曲线密码学的关键基石。