

十大经典数据挖掘算法—Apriori
编程实验
描述
1. 关联分析
关联分析是一类非常有用的数据挖掘方法,能从数据中挖掘出潜在的关联关系。比如,在著名的购物篮事务(market basket transactions)问题中,
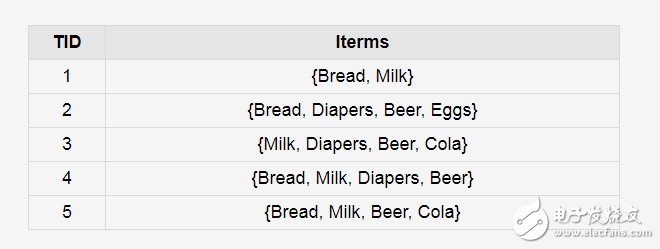
关联分析则被用来找出此类规则:顾客在买了某种商品时也会买另一种商品。在上述例子中,大部分都知道关联规则:{Diapers} → {Beer};即顾客在买完尿布之后通常会买啤酒。后来通过调查分析,原来妻子嘱咐丈夫给孩子买尿布时,丈夫在买完尿布后通常会买自己喜欢的啤酒。但是,如何衡量这种关联规则是否靠谱呢?下面给出了度量标准。
支持度与置信度

对于靠谱的关联规则,其支持度与置信度均应大于设定的阈值。那么,关联分析问题即等价于:对给定的支持度阈值min_sup、置信度阈值min_conf,找出所有的满足下列条件的关联规则:
支持度>=min_sup
置信度>=min_conf
把支持度大于阈值的项集称为频繁项集(frequent itemset)。因此,关联规则分析可分为下列两个步骤:
生成频繁项集F=X∪Y;
在频繁项集F中,找出所有置信度大于最小置信度的关联规则X⟶Y。
暴力方法
若(对于所有事务集合)项的个数为d,则所有关联规则的数量:
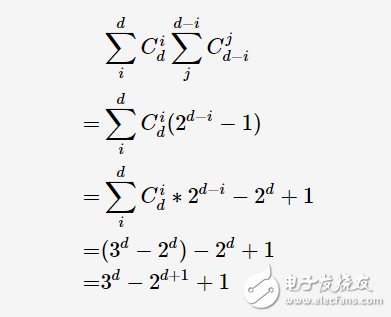
如果采用暴力方法,穷举所有的关联规则,找出符合要求的规则,其时间复杂度将达到指数级。因此,我们需要找出复杂度更低的算法用于关联分析。
2. Apriori算法Agrawal与Srikant提出Apriori算法,用于做快速的关联规则分析。
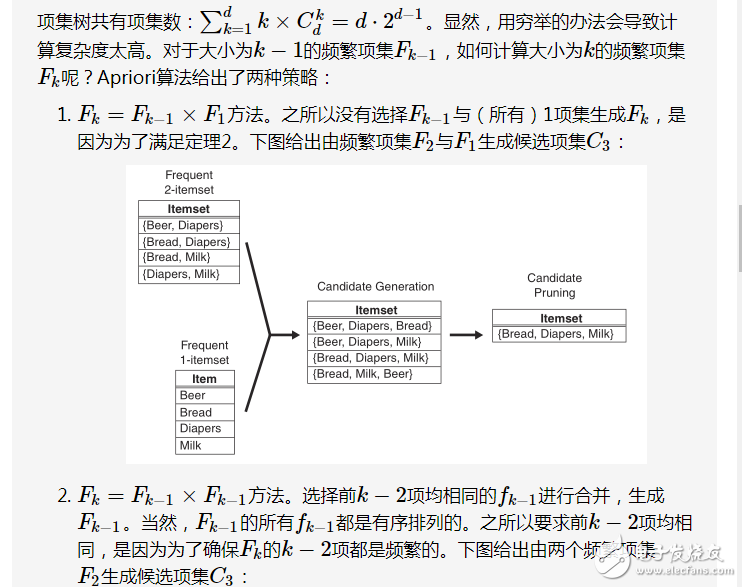
频繁项集生成
根据支持度的定义,得到如下的先验定理:
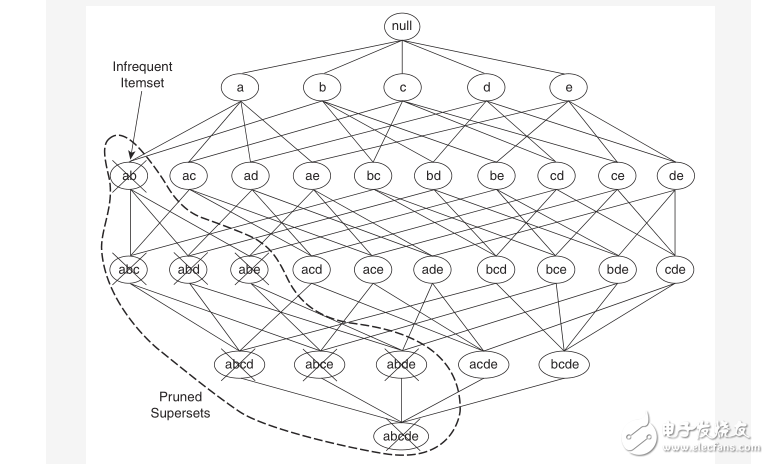
定理1:如果一个项集是频繁的,那么其所有的子集(subsets)也一定是频繁的。
这个比较容易证明,因为某项集的子集的支持度一定不小于该项集。
定理2:如果一个项集是非频繁的,那么其所有的超集(supersets)也一定是非频繁的。
定理2是上一条定理的逆反定理。根据定理2,可以对项集树进行如下剪枝:
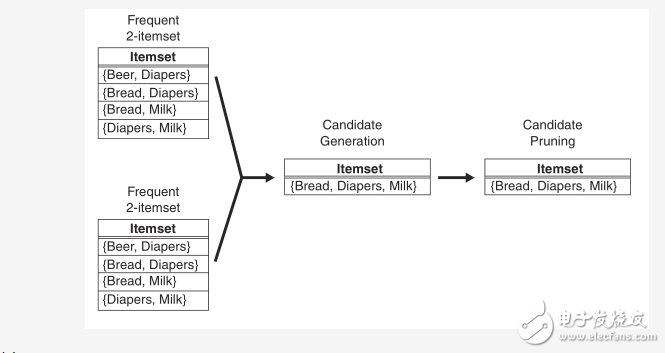
关联规则生成
关联规则是由频繁项集生成的,即对于FkFk,找出项集hmhm,使得规则fk−hm⟶hmfk−hm⟶hm的置信度大于置信度阈值。同样地,根据置信度定义得到如下定理:
定理3:如果规则X⟶Y−X不满足置信度阈值,则对于X的子集X′,规则X′⟶Y−X′也不满足置信度阈值。
根据定理3,可对规则树进行如下剪枝:
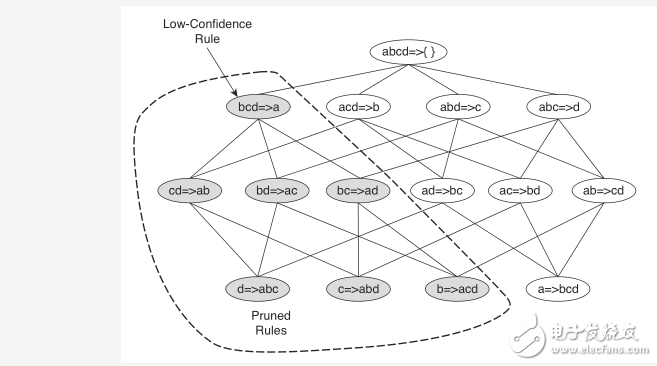
关联规则的生成算法如下:

-
机器学习的基本流程和十大算法2023-10-31 1651
-
关于数据挖掘的十种算法原理讲解2023-09-18 1876
-
一文弄懂数据挖掘的十大算法,数据挖掘算法原理讲解2023-09-14 2260
-
数据挖掘十大算法2023-08-17 3362
-
C语言动图演示十大经典排序算法(含代码)2023-01-29 1988
-
数据挖掘十大经典算法,你都知道哪些!2018-11-06 5485
-
从五个方面让你了解人工智能算法中的Apriori2018-07-05 2671
-
十大经典机器学习算法之一--Apriori2018-06-25 11868
-
数据挖掘Apriori算法报告2018-02-04 5393
-
数据挖掘常用的十大算法2017-12-29 27566
-
数学建模十大经典算法2016-08-08 1446
-
数据挖掘Apriori算法的改进2013-08-19 1116
-
关联规则Apriori算法的改进2011-05-13 938
-
电池管理中的十大经典理论2009-11-06 945
全部0条评论

快来发表一下你的评论吧 !

