基数排序是怎么排的_基数排序详细过程

计数排序

学习基数排序之前首先学习计数排序。

计数排序假设每个元素都是在0到k之间的一个整数。

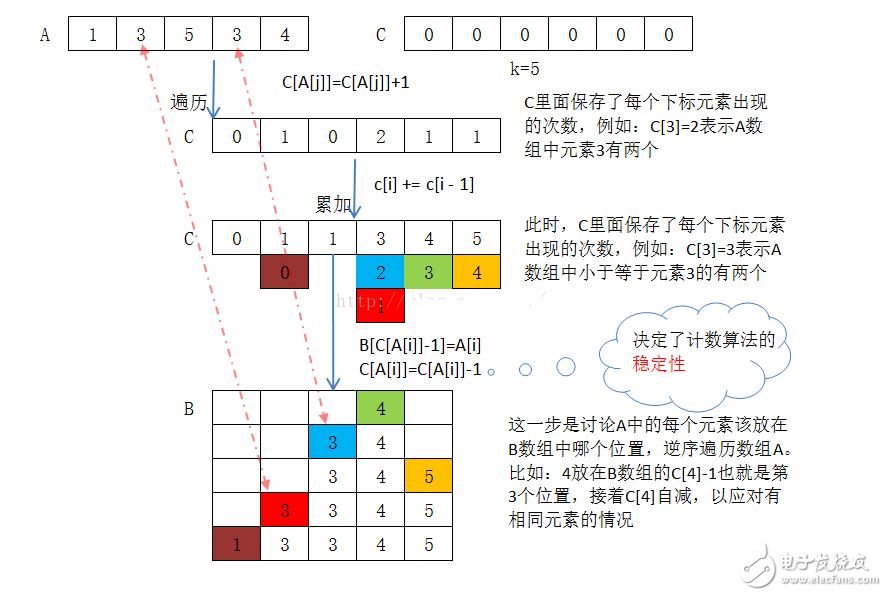
基数排序的基本思想，对于每个元素x，如果我们知道了小于x的元素的个数，就可以确定输出数组中元素x的位置，那么直接将元素x放到输出数组中。比如有3小于x的元素，那在输出数组中，x肯定位于第4个位置。

计数排序的算法用伪代码描述为：

COUNTING-SORT（A，k）

// 初始化数组C

for i=0 to k

C［i］=0

// 统计A［j］元素出现的次数，保存到C数组中

for j=0 to A.length

C［A［j］］=C［A［j］］+1

// 统计小于等于A［j］元素的个数

for k=0 to k

C［K］=C［K-1］+C［K］

// 将A中的元素放在B中正确的位置

for i=A.length to 0

B［C［A［i］］-1］=A［i］

C［A［i］］=C［A［i］］-1

注：由于有可能有相同元素存在，所以，每次将A［i］元素放入B数组中，都要将C［A［j］］的值减一，这样当遇到下一个值等于A［j］的元素时，该元素就能放在输出数组中A［j］的前面。

计数排序的详细过程如下

 

计数排序的关键代码如下

public int［］ countSort（int a［］， int k） {

int［］ b = new int［a.length］;

int［］ c = new int［k］;

for （int i = 0; i

c［i］ = 0;

}

for （int i = 0; i

c［a［i］］ += 1;

}

for （int i = 0; i

if （i ！= 0） {

c［i］ += c［i - 1］;

}

}

for （int i = a.length - 1; i >= 0; i--） {

b［c［a［i］］ - 1］ = a［i］;

c［a［i］］ = c［a［i］］ - 1;

}

return b;

}

计数排序的性能

很容易得到计数排序的时间复杂度为：T（n）=O（k+n），因此当k小于等于n，也就是当k=O（n），k和n同阶时，采用计数排序的时间复杂度为T（n）=O（n）

同时，计数排序也是一种稳定的排序算法。

基数排序

基数排序最初是用在打孔卡片制表机上的一种排序算法，由Herman Hollerith发明，也就是IBM的创始人。

基数排序从最低为开始来排序的，从低位到高位，按位排序，按位排序必须是稳定的。

基数排序的详细过程

 

基数排序算法描述为

RADIX-SORT（A，d）

for i=1 to d

use a stable sort to sort arrat A on digit i

在这里我们选择计数排序。考虑常规情况，对［0.。.9］之间的数排序，k=10，且一般有k<

基数排序的关键代码，这里以数组排序时按照十进制每位进行比较。

/**

* 基数排序

* @param result 最终已排序的数组，共用一个节省空间

* @param maxLen 待排序的数组中最大的位数

*/

public static void radixSort（int［］ a，int［］ result， int maxLen） {

int flag = 1;

// 保存每轮要排序的位对应数组a的值

int ［］ digitArr = new int［a.length］;

for（int i=0; i

// 共比较的轮数

flag *= 10;

// b数组中对应的装着a数组中每位的数，第一轮装着各位，第二轮装着十位数。。.

for （int j = 0; j < digitArr.length; j++） {

digitArr［j］=a［j］%flag;

digitArr［j］=digitArr［j］/（flag/10）;

}

countSort（a， digitArr，result，10）;

// 每一轮计数排序完后刷新下一轮要排序的数组

System.arraycopy（result， 0， a， 0，result.length）;

}

}

调用计数排序的函数

/**

* 计数排序 ：对数组a中的元素按某些位排序

* @param tmp 要参与排序的当前位的值保存在tmp中

* @param result 每次计数排序后的新的数组顺序

*/

public static void countSort（int a［］， int tmp［］， int result［］， int k） {

int［］ c = new int［k］;

for （int i = 0; i < c.length; i++） {

c［i］ = 0;

}

for （int i = 0; i

c［tmp［i］］ += 1;

}

for （int i = 0; i < c.length; i++） {

if （i ！= 0） {

c［i］ += c［i - 1］;

}

}

for （int i = tmp.length - 1; i >= 0; i--） {

// 和计数排序唯一的差别在于赋值的时候用真实的数据

result［c［tmp［i］］ - 1］ = a［i］;

c［tmp［i］］ = c［tmp［i］］ - 1;

}

}

基数排序的性能

如果基数排序使用的稳定排序算法的时间复杂度为O（n+k），那么基数排序的时间复杂度为T（n）=O（d（n+k））

很容易理解要循环d轮，每轮耗时为O（n+k），于是总的耗时为O（d（n+k））

在此基础上，从2^r进制来看，此时k为2^r，并且一个b位数要比较b/r轮。于是我们得到T（n）=O（（b/r）（n+2^r））

对上式求导可得其最小值。此时r=lgn，此时T（n）=O（（b/lgn）n），如果再取b=lgn，这时就能达到最少的运行时间，时间复杂度为T（n）=O（n）

基数排序也是稳定的排序算法