基数排序知识点全面概括

 数据背景

在基数排序中，我们不能再只用一位数的序列来列举示例了。一位数的序列对基数排序来说就是一个计数排序。

这里我们列举无序序列 T = ［ 2314， 5428， 373， 2222， 17 ］

排序原理

上面说到基数排序不需要进行元素的比较与交换。如果你有一些算法的功底，或者丰富的项目经验，我想你可能已经想到了这可能类似于一些“打表”或是哈希的做法。而计数排序则是打表或是哈希思想最简单的实现。

计数排序

计数排序的核心思想是，构建一个足够大的数组 hashArray［］，数组大小需要保证能够把所有元素都包含在这个数组上 。

假设我们有无序序列 T = ［ 2314， 5428， 373， 2222， 17 ］

首先初始化数组 hashArray［］ 为一个全零数组。当然，在 Java 里，这一步就不需要了，因为默认就是零了。

在对序列 T 进行排序时，只要依次读取序列 T 中的元素，并修改数组 hashArray［］ 中把元素值对应位置上的值即可。这一句有一些绕口。打个比方，我们要把 T［0］ 映射到 hashArray［］ 中，就是 hashArray［T［0］］ = 1. 也就是 hashArray［2314］ = 1. 如果序列 T 中有两个相同元素，那么在 hashArray 的相应位置上的值就是 2。

下图是计数排序的原理图：

（假设有无序序列：［ 5， 8， 9， 1， 4， 2， 9， 3， 7， 1， 8， 6， 2， 3， 4， 0， 8 ］）

 

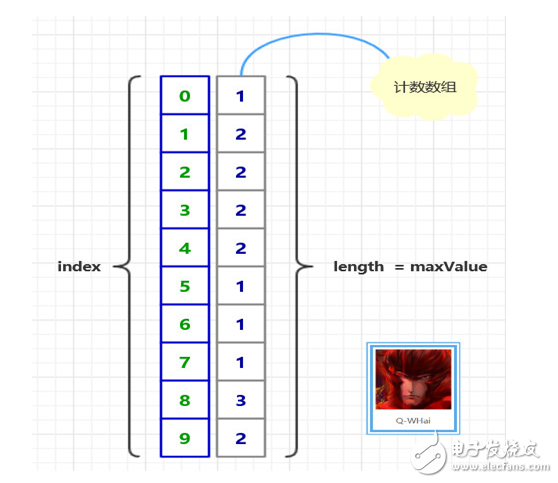
基数排序原理图

上面的计数排序只是一个引导，好让你可以循序渐进地了解基数排序。

 

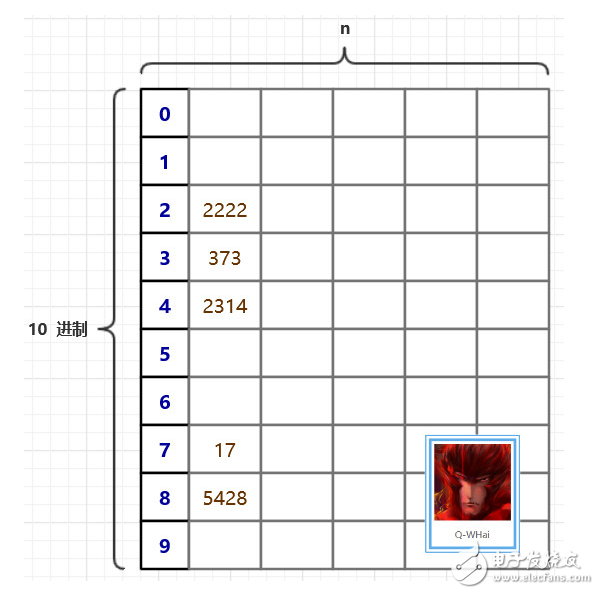
上面这幅图，或许你已经在其他的博客里见到过。这是一个很好的引导跟说明。在基数排序里，我们需要一个很大的二维数组，二维数组的大小是 （10 * n）。10 代表的是我们每个元素的每一位都有 10 种可能，也就是 10 进制数。在上图中，我们是以每个数的个位来代表这个数，于是，5428 就被填充到了第 8 个桶中了。下次再进行填充的时候，就是以十位进行填充，比如 5428 在此时，就会选择以 2 来代表它。

 

算法优化

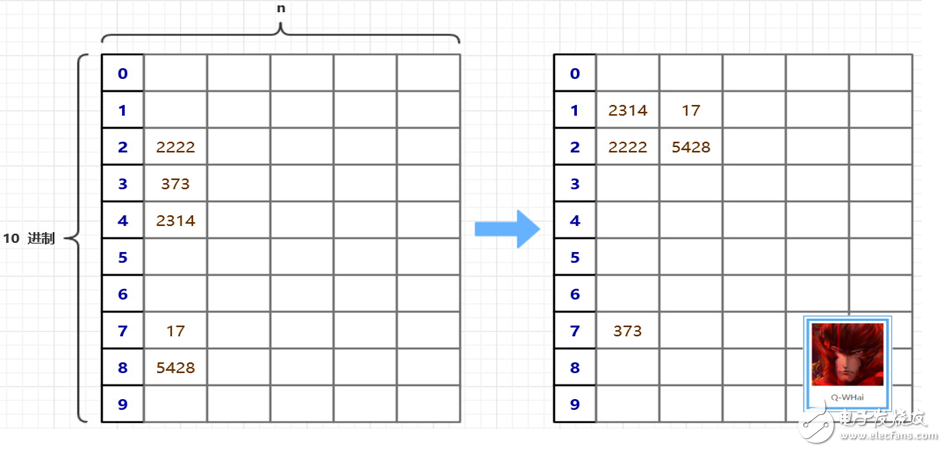
在算法的原理中，我们是以一张二维数组的表来存储这些无序的元素。使用二维数组有一个很明显的不足就是二维数组太过稀疏。数组的利用率为 10%。

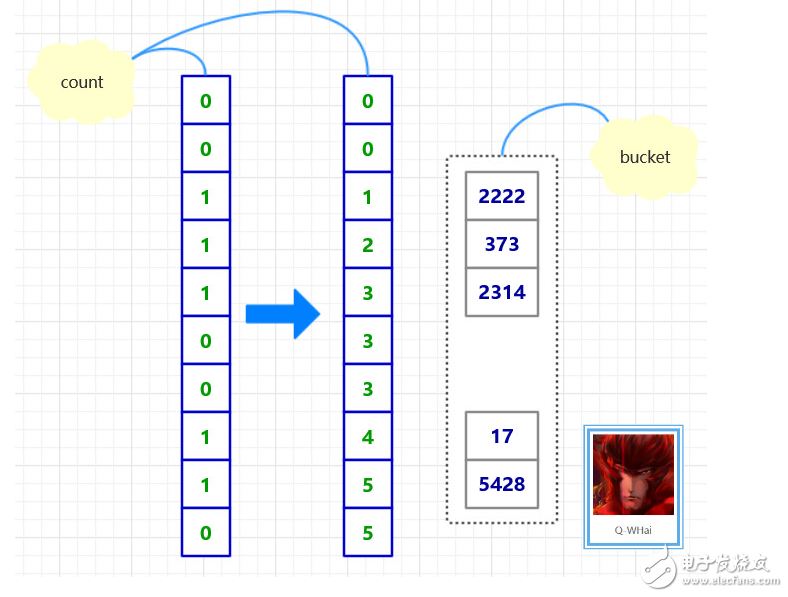
在寻求优化的路上，我们想到一种可以压缩空间的方法，且时间复杂度并没有偏离得太厉害。那就是设计了两个辅助数组，一个是 count［］，一个是 bucket［］。count 用于记录在某个桶中的最后一个元素的下标，然后再把原数组中的元素计算一下它应该属于哪个“桶”，并修改相应位置的 count 值。直到最大数的最高位也被添加到桶中，或者说，当所有的元素都被被在第 0 个桶中，基数排序就结束了。

优化后的原理图如下：

 

算法实现

import org.algorithm.array.sort.interf.Sortable;

/**

*

* 基数排序/桶排序

* 

*

* @author Q-WHai

* @see http://blog.csdn.net/lemon_tree12138

* @version 0.1.1

*/

public class RadixSort implements Sortable {

@Override

public int［］ sort（int［］ array） {

if （array == null） {

return null;

}

int maxLength = maxLength（array）;

return sortCore（array， 0， maxLength）;

}

private int［］ sortCore（int［］ array， int digit， int maxLength） {

if （digit >= maxLength） {

return array;

}

final int radix = 10; // 基数

int arrayLength = array.length;

int［］ count = new int［radix］;

int［］ bucket = new int［arrayLength］;

// 统计将数组中的数字分配到桶中后，各个桶中的数字个数

for （int i = 0; i < arrayLength; i++） {

count［getDigit（array［i］， digit）］++;

}

// 将各个桶中的数字个数，转化成各个桶中最后一个数字的下标索引

for （int i = 1; i < radix; i++） {

count［i］ = count［i］ + count［i - 1］;

}

// 将原数组中的数字分配给辅助数组 bucket

for （int i = arrayLength - 1; i >= 0; i--） {

int number = array［i］;

int d = getDigit（number， digit）;

bucket［count［d］ - 1］ = number;

count［d］--;

}

return sortCore（bucket， digit + 1， maxLength）;

}

/*

* 一个数组中最大数字的位数

*

* @param array

* @return

*/

private int maxLength（int［］ array） {

int maxLength = 0;

int arrayLength = array.length;

for （int i = 0; i < arrayLength; i++） {

int currentLength = length（array［i］）;

if （maxLength < currentLength） {

maxLength = currentLength;

}

}

return maxLength;

}

/*

* 计算一个数字共有多少位

*

* @param number

* @return

*/

private int length（int number） {

return String.valueOf（number）.length（）;

}

/*

* 获取 x 这个数的 d 位数上的数字

* 比如获取 123 的 0 位数，结果返回 3

*

* @param x

* @param d

* @return

*/

private int getDigit（int x， int d） {

int a［］ = { 1， 10， 100， 1000， 10000， 100000， 1000000， 10000000， 100000000， 1000000000 };

return （（x / a［d］） % 10）;

}

}

基数排序过程图

如果我们的无序是 T = ［ 2314， 5428， 373， 2222， 17 ］，那么其排序的过程就如下两幅所示。

基数排序过程图-1

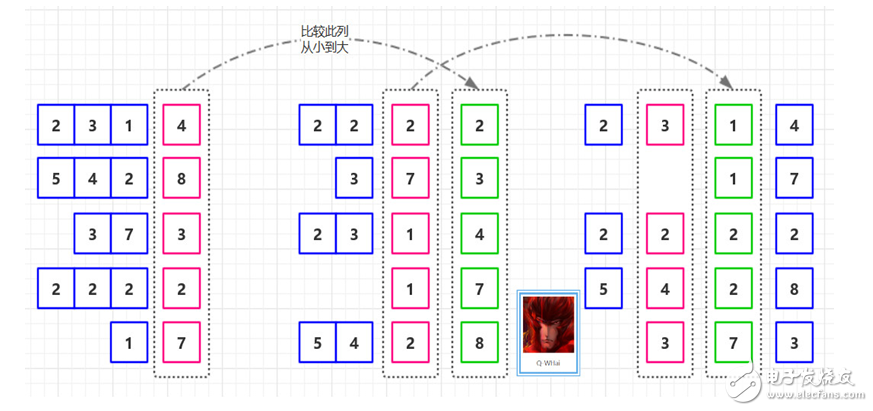
基数排序过程图-2

 

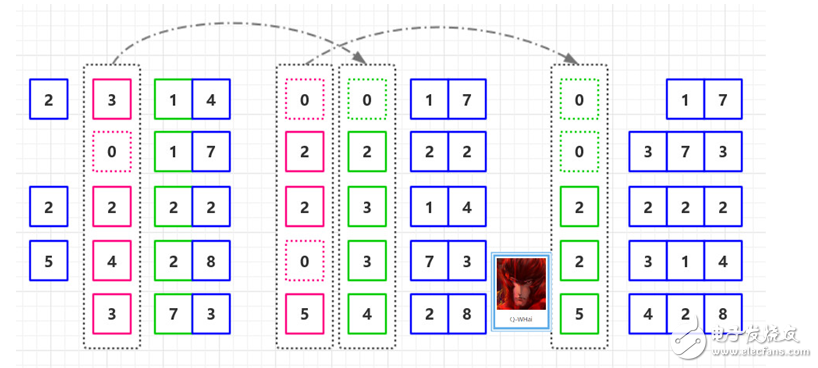
复杂度分析

 

其中，d 为位数，r 为基数，n 为原数组个数。

在基数排序中，因为没有比较操作，所以在复杂上，最好的情况与最坏的情况在时间上是一致的，均为 O（d * （n + r））。