无线传感器网络吞吐量的自适应跨层优化策略

引言

吞吐量是无线传感器网络（Wireless Sensor Network，WSN）的一项重要性能指标，它直接反映了无线传感器网络工作运行的效率，如何提高吞吐量一直都是无线传感器网络研究的热点。

R.J.Lavery在参考文献中首次建立了经典的Adhoc网络点对点链路模型，明确了点对点链路模型吞吐量的数学定义式。作者以吞吐量为优化目标，针对影响吞吐量的符号速率和数据包长度这两个参数分别作了优化，得到了不同条件下的最优符号速率和数据包长。随后Taesang Yoo等人在参考文献中提出了一种数学框架，采用符号速率、数据包长度、调制星座体积3个参数作为优化变量，实现了MQAM调制方式下点对点链路吞吐量的优化。其后的参考文献基于参考文献提出的模型和假设，对链路的吞吐量也作了类似的研究和优化分析。但是参考文献的吞吐量优化都是基于参考文献建立的Ad hoc网络点对点链路模型，而目前针对无线传感器网络吞吐量的研究相对较少。

针对上述问题，本文将针对在WSN中如何最大化点对点链路吞吐量这一问题展开研究。为了最大化吞吐量，本文采用跨层优化机制，不仅考虑了符号速率和调制星座体积这两个物理层（PHY）主要参数，还考虑了MAC层的数据包长度，通过PHY和MAC层参数的联合优化，保证在不同通信距离下链路的吞吐量能够达到最优。

1系统模型和假设

为了简化分析，本文只考虑WSN中两个通信节点之间的点对点链路。WSN中点对点通信链路一般由单个的发射机、接收机以及无线通信信道组成。假定发射机节点发送的每个数据包总长为K+C=L位，其中K为有用信息数据长度，C为循环冗余校验码CRC（Cyclical Redundancy Che ck），用来检测每个数据包中的误码，在本文的仿真分析中C=16位。接收机节点使用CRC校验接收到的数据包。假定CRC只进行检错而没有进行纠错编码，并且CRC有足够的冗余度可以检测到每个数据包的所有误码。当接收机接收到的数据包中不包含误码时，便发送一个ACK反馈帧给发射机，告之数据已经正确接收；否则发送一个NACK反馈帧。当发送节点接收到NACK帧时，便重传该数据包，否则传送下一个新的数据包。在实时通信中，ACK仍有可能产生误码，从而导致系统的吞吐量下降。为了简单起见，这里假定ACK/NACK反馈帧在传输过程中不会出现误码。

根据参考文献，点对点链路的吞吐量可以定义为：每秒成功接收到的有用信息比特数。对于一个基于上述模型和假设条件的点对点传输链路，其吞吐量通式为：

其中，b为每个调制符号所包含的比特数，Rs为符号速率，f（b，rs，L）为包成功传送率（PSR），它定义为正确地接收到一个数据帧的概率。PSR由下式给出：

其中Pr为信号接收功率，N0为AWGN信道中噪声的半边功率谱密度。

同时，接收信噪比定义为：SNR=Pr/（N0.B） （4）

其中B=1 MHz为系统带宽。比较式（3）、（4），可以得到符号信噪比rs与接收信噪比SNR之间的关系为：

2吞吐量分层优化

2.1物理层参数优化

2.1.1符号速率优化

为了找到最优符号速率，以使得链路的吞吐量达到极大值，对式（1）求关于Rs的偏导数并令该导数为0，即令，可以得到如下关于rs的微分方程：

图1给出了4种不同符号速率条件下，吞吐量与SNR的关系曲线。可以看出，当SNR较高时，链路能够支持较高的符号速率，从而获得较大的吞吐量；然而当SNR低于一定值时，吞吐量迅速减小，此时应采用较低符号速率以维持一定的吞吐量。因此，在实际的通信系统中，为了得到最优吞吐量，必须根据SNR进行自适应速率调整。根据式（8）可求解得到当L=100、b=2时，。当SNR发生变化时，应根据式（9）来调节数据速率Rs，确保，以保证得到最优吞吐量。据此得到的最优吞吐量曲线如图1所示。

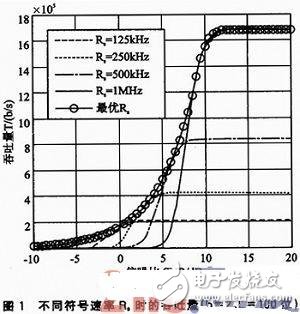
2.1.2调制星座体积优化

从式（7）、（8）可以看到，调制星座体积b对Pe、rs也有影响，因而链路的最优吞吐量也取决于调制星座体积的大小。同样，对式（1）求关于b的偏导数，并令，可得：

由上式可知，b*取决于L、Pe和rs，而时，b*仅取决于L和Pe；根据不同调制方式下的误符号率Pe，通过求解（10）式，可得该调制方式下的b*.

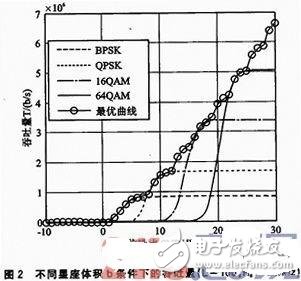
图2显示了不同信噪比条件下，星座体积b对吞吐量的影响。由图2可见，当信道条件较好，即SNR较大时，可以让每个符号承载更多的信息位，即采用高阶调制方式来提高系统的吞吐量；而当信道条件较差即SNR较小时，误符号率较大，此时应该采用低阶调制方式，以保证最优吞吐量。

2.2 MAC层优化

在Rs及其他系统参数一定的条件下，可以找到一个使吞吐量最大的包长，称为最优数据包长度，记做L*.L*可以用求极值的方法得到，对式（1）求关于L的偏导数，令，可求解得到最优数据包长度：

图3比较了在不同SNR、不同包长L条件下链路吞吐量。如图3所示，当SNR较大时，包长越大，吞吐量越大。这是因为，较近的通信距离使得信道条件比较好，信噪比较大，误包率非常小，f（b，rs，L）≈1.此时吞吐量T≈bRs（L—C）/L，即吞吐量与SNR无关，而是随着L的增大而增大。但是吞吐量不会随着L的增大而无限增大，当L》》C时，T≈b.Rs，即T的上限值为b.Rs.以上两点结论均可从图3中得到很好的验证。但是L不宜过大，因为若L过大，可能会引入其他的问题，譬如延时等。因此，要权衡时延等因素而选取一个尽可能大的数据包长度L，在本文仿真中设定最大包长Lmax=512.

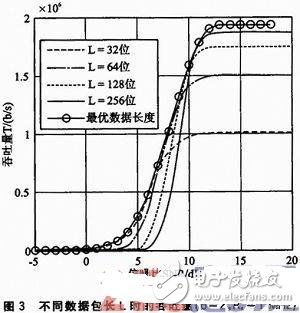
然而，从图3中还可以看到，随着SNR低于一定值时，吞吐量迅速下降为0.此时，求解式（11）得到不同通信距离下相应的最优数据包长L（d）*，进而得到吞吐量的最优曲线，如图3所示。从最优曲线可以看到，当SNRT（L）》T（Rs）；而当SNR低于一定值后，优化后的吞吐量的大小关系为T（Rs）》T（b）》T（L）。特别地，当SNR2dB）和较低信噪比（SNR2 dB）区：在此区域内信道条件相对较好，误符号率很低，应尽可能采用高的符号速率；但由于受系统带宽的限制，Rs≤B，所以单方面通过增大符号速率并不能使吞吐量达到最优。此时，可以通过让每个符号承载更多的位信息，即采用高阶调制方式以提高系统的吞吐量并联合最优数据包长，可使吞吐量达到最优。最优参数对（b*，L*）可以通过联立求解式（10）、（11）得到。