基于光线追踪实现反射折射效果

本文翻译自Scratchapixel 3.0[1]，是一个关于计算机图形学的系统性的学习教程。如果有误，欢迎在评论区讨论。

光线追踪的另一个优点是，通过扩展光线传播的思想，我们可以非常容易地「模拟反射」和「折射」等效果，这在模拟玻璃材料或镜面表面时非常方便。在一篇名为《用于阴影显示的改进照明模型》的 1979 年论文中，Turner Whitted 首次描述了如何扩展 Appel 的光线追踪算法以进行更高级的渲染。Whitted 的想法扩展了 Appel 发射光线的模型，以包括反射和折射的计算。

在光学中，反射和折射是众所周知的现象。虽然后面的课程将专门讲解反射和折射，但我们将研究模拟它们所需的内容。我们将以具有折射和反射特性的玻璃球为例。只要我们知道与球相交的光线的方向，就很容易计算它发生的情况。反射和折射方向都基于交点处的法向量和入射光线（主光线）的方向。为了计算折射方向，我们还需要指定材料的折射率。虽然我们之前说过光线直线传播，但我们可以将折射可视化为光线弯曲。当光子撞击不同介质（因此折射率不同）的物体时，其方向会改变。这个科学将在后面更深入地讨论。只要我们记住这两个效应取决于法向量和入射光线方向，而折射取决于材料的折射率，我们就可以继续前进。同样，我们还必须意识到像玻璃球这样的物体同时具有反射和折射性质。我们需要计算给定表面上的两者，但是我们如何混合它们？我们将反射结果的 50％与折射结果的 50％混合吗？不幸的是，它比那更复杂。值的混合取决于主光线（或视角方向）和物体法线以及折射指数之间的角度。幸运的是，一个方程可以精确地计算每个值应该如何混合。这个方程被称为菲涅耳方程。为了保持简洁，我们现在只需要知道它的存在，并将帮助确定混合值。

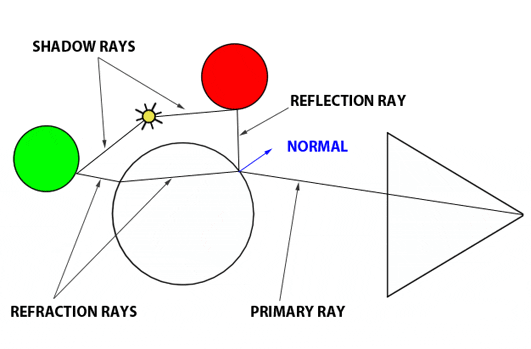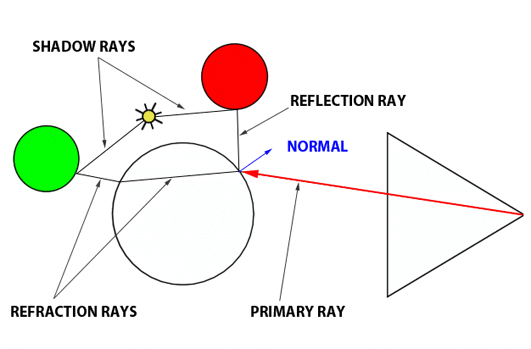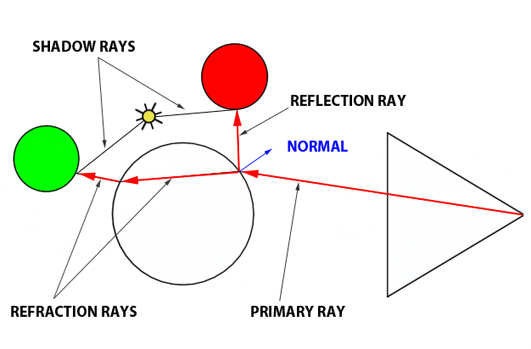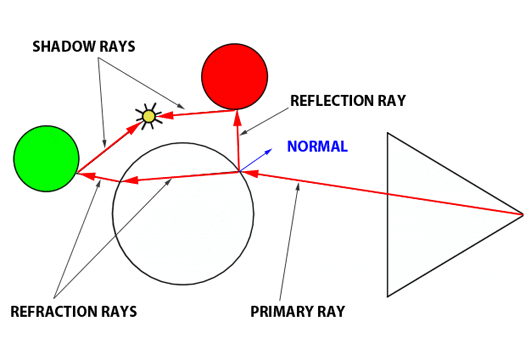
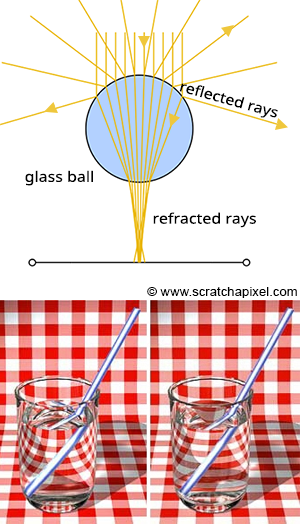
图1：使用光学定律计算反射和折射光线。

让我们回顾一下。Whitted 算法如何工作？我们从眼睛发射主光线，并与场景中的物体最近的交点（如果有）相交。如果光线击中不是漫反射或不透明的物体，我们必须进行额外的计算工作。为了计算例如玻璃球上的那个点的结果颜色，你需要计算反射颜色和折射颜色并将它们混合。记住，我们需要分三步进行。计算反射颜色，计算折射颜色，然后应用菲涅耳方程。

首先，我们计算反射方向。为此，我们需要两个项目：交点处的法向量和主光线的方向。一旦我们获得反射方向，我们发射一个新光线。回到我们的旧例子，假设反射光线击中了红色球。使用 Appel 的算法，我们通过向光源发射阴影光线来确定达到红色球上那个点的光线量。这将获得颜色（如果被遮挡则为黑色），乘以光强度并返回到玻璃球的表面。

现在，我们对折射做同样的事情。因为光线穿过了玻璃球，所以它被称为传输光线（光线从球的一侧传输到另一侧；已传输）。为了计算传输方向，我们需要交点处的法向量，主光线方向和材料的折射率（在这个例子中，它可能是类似于玻璃材料的 1.5）。使用计算出的新方向，折射光线继续到玻璃球的另一侧。在那里，因为它改变了介质，所以光线又被折射了一次。正如你在相邻的图像中看到的那样，当光线进入和离开玻璃物体时，光线的方向会改变。每当有介质变化时都会发生折射，而光线退出的介质和进入的介质具有不同的折射率。空气的折射率非常接近 1，而玻璃的折射率约为 1.5。折射会使物体在看不同折射率的物体时或通过不同折射率的物体看时出现偏移。假设当折射光线离开玻璃球时，它击中了绿色球。我们通过发射阴影光线计算了绿色球和折射光线之间的交点处的局部照明。然后，将颜色（如果被遮挡则为黑色）乘以光强度并返回到玻璃球的表面。

最后，我们计算菲涅耳方程。我们需要玻璃球的折射率，主光线与命中点法线之间的角度。使用点积（我们将在稍后解释），菲涅耳方程返回两个混合值。

以下是一些伪代码，以加强它的工作方式：

•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  

// compute reflection colorcolor reflectionCol = computeReflectionColor();
// compute refraction colorcolor refractionCol = computeRefractionColor();
float Kr; // reflection mix valuefloat Kt; // refraction mix value
fresnel(refractiveIndex, normalHit, primaryRayDirection, &Kr, &Kt);
// mix the two colors. Note that Kt = 1 - KrglassBallColorAtHit = Kr * reflectionColor + Kt * refractionColor;

在上面的代码中，我们在注释中写道Kt = 1 - Kr。换句话说，Kr + Kt = 1。这是因为在自然界中，光线不能被创造或摧毁。因此，如果一些入射光被反射，那么剩余的入射光（未被反射的部分）必然会被折射。如果你将反射和折射光的总和相加，它等于入射光的量。通常，菲涅耳方程为我们提供了Kr和Kt的值（如果它做正确的事情，它们的总和应该等于 1），因此你可以直接使用函数返回的值。然而，如果我们只有其中一个，这就足够了。如果你有Kr，你可以得到Kt（1-Kr）。如果你有Kt，你可以得到Kr（1-Kt）。

这个算法最后一个美妙的事情是它是「递归」的（这在某种程度上也是一种诅咒！）。在我们研究的情况下，反射光线击中了一个红色的不透明球体，折射光线击中了一个绿色的、不透明的、散射的球体。然而，我们会想象红色和绿色的球体也是玻璃球。要找到反射和折射光线返回的颜色，我们必须对红色和绿色球体使用与原始玻璃球相同的过程：也就是说，向场景中射入更多的反射和折射光线。这是射线跟踪算法的一个缺点，有时会成为一个头痛的问题。想象一下我们的相机在一个只有反射面的盒子里。理论上，光线被困住了，将会无限地反弹在盒子的墙壁上（或者直到你停止模拟）。因此，我们必须设置一个任意的限制，防止光线相互作用，从而无限递归。每次光线反射或折射时，它的深度都会增加。当光线深度大于最大递归深度时，我们停止递归过程。你的图像不一定会看起来完全准确，但是有一个近似的结果总比没有结果好。