最新图优化框架,全面提升SLAM定位精度

0. 这篇文章干了啥？

同时定位与地图构建（SLAM）是一项关键技术，允许移动机器人在部分或完全未知的环境中自主导航。它包括使用机载传感器同时估计机器人状态和构建传感器检测到的环境地图。SLAM可以根据传感器和地图构建技术的类别进行分类，如视觉SLAM、激光SLAM、惯性SLAM等。

解决SLAM问题的经典方法可以分为基于滤波的方法和基于图的方法。在1986年提出SLAM问题的前二十年里，基于概率公式的滤波方法已经实现了准确的估计。然而，在大规模问题中更新协方差矩阵在计算上是昂贵的。基于图的方法最早由Lu和Milios在1997年引入，随着图的增长，计算成本较低。随着计算能力的提高，基于图的SLAM的优化算法相比经典的滤波方法（如扩展卡尔曼滤波、Rao-Blackwellized粒子滤波和信息滤波）获得了广泛关注。Wilbers等人展示了基于图的方法在定位方面比粒子滤波具有更高的精度。

姿态图优化（PGO）可以建模为一个非凸优化问题，是基于图的SLAM的基础，其中它将每个姿态与一个顶点关联，将每个测量与图的一条边关联，需要从有噪声的相对测量中估计多个未知姿态。在三维空间中的姿态通常包括旋转和平移，旋转可以使用欧拉角、轴角（so(3)）、特殊正交群（SO(3)）或四元数（Q）表示，平移由一个三维向量t指定。此外，整体姿态还可以使用特殊欧氏群（SE(3)）、李代数（se(3）或双四元数（DQ）表示。不同的建模方法会产生不同的约束，如在se(3)中没有约束，在SE(3)中有矩阵正交和行列式约束，或在Q中有球面约束。选择与问题结构兼容的简单表示将导致一个更容易解决和更准确的模型。

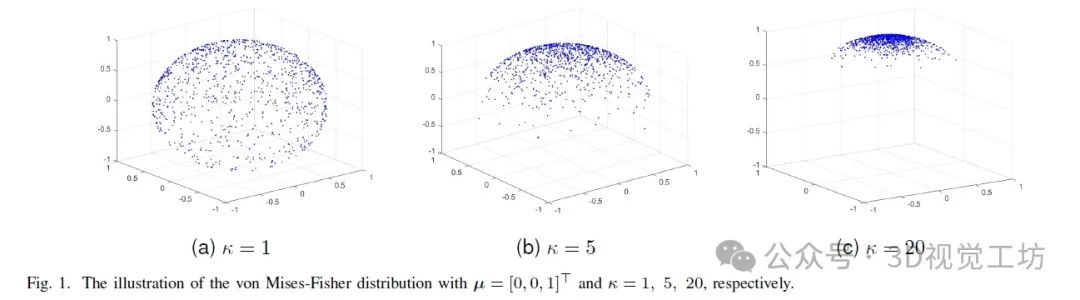
在过去的二十年中，许多模型已经根据噪声的不同统计分布和姿态表示方法得到了发展。同时，也提出了许多高效的优化算法来解决这些模型。从模型的角度来看，旋转噪声的统计分布通常分为高斯分布或各向同性的冯米塞斯-费舍尔（vMF）分布，而平移噪声统一表现为高斯噪声。基于最大似然估计，在se(3)上的高斯噪声可以直接导出一个无约束的非线性最小二乘模型。同样，Cheng等人建立了基于单位双四元数的最小二乘模型，并提出了一种更有效的方法来计算雅可比矩阵。通过消除两个变量，他们的模型也是无约束的。另一种建模方法使用SO(3)表示旋转，假定其服从vMF分布，并导出具有正交和行列式约束的模型。由于se(3)需要转换来描述运动过程，用SO(3)或Q和一个三维向量表示的目标函数的表达式相比无约束模型更简洁；然而，约束的引入增加了挑战。

从算法的角度来看，提出了几种高效且准确的方法来解决SLAM中的大规模问题。诸如随机梯度下降等一阶优化方法可以减少梯度计算的复杂性，并有效地解决无约束优化问题。收敛速度更快的算法，如高斯-牛顿方法、Levenberg--Marquardt方法、信赖域方法也被引入来解决该问题。与计算矩阵逆不同，使用QR或Cholesky分解等矩阵分解技术来降低复杂性，并提出了增量版本。Grisetti等人和Wagner等人提出了基于流形的高斯-牛顿算法，其中雅可比矩阵具有稀疏结构，更新过程避免了大规模线性方程系统的昂贵存储。

然而，二阶算法仅在局部区域具有快速收敛率，对于非凸问题通常返回局部极小值。后来的工作集中于找到更好的初始点并确认解的最优性。Rosen等人提出了一种基于Powell的Dog-Leg信赖域方法的稳健增量最小二乘估计，并提高了数值稳定性。Carlone等人通过检查对偶间隙推导了一个带约束的二次规划并验证了最优解。通过扩展可行集到其凸闭包，一种凸松弛方法有效地克服了非凸问题初始点选择的难题。此外，Rosen等人将模型松弛为一个半定规划，并证明了只要噪声低于某个临界阈值，其松弛的最小化结果提供了一个精确的最大似然估计。Fan和Murphey提出了PGO的一个上界，并通过广义近端方法解决它，该方法可以收敛到一阶临界点且不依赖于黎曼梯度。另一种找到更好局部极小值或全局极小值的方法依赖于初始化技术。他们指出非凸旋转估计是SLAM困难的真正原因，平移对旋转估计影响较小。因此，计算一个好的旋转估计将提高算法的性能。

我们提出了一种非凸姿态图优化的近端线性化黎曼交替方向乘子法（PieADMM），它使用最新的部分信息更新其他变量。我们的子问题不仅具有闭式解，而且可以并行计算，从而使每次更新的时间复杂性较低。这一优势在大规模数值实验中得到了验证。从理论上讲，收敛性分析补充了我们的发现。

下面一起来阅读一下这项工作~

1. 论文信息

标题：Non-convex Pose Graph Optimization in SLAM via Proximal Linearized Riemannian ADMM

作者：Xin Chen, Chunfeng Cui, Deren Han, Liqun Qi

机构：北京航空航天大学

原文链接：https://arxiv.org/abs/2404.18560

2. 摘要

位姿图优化 (PGO) 是解决基于位姿的同时定位与地图构建 (SLAM) 问题的一种著名技术。在本文中，我们使用单位四元数和三维向量表示旋转和平移，并提出了一种基于冯·米塞斯-费舍尔分布的新型 PGO 模型。从单位四元数导出的约束是球面流形，投影到这些约束上可以通过归一化来计算。然后，我们开发了一种近端线性化黎曼交替方向乘子法 (PieADMM) 来解决所提出的模型，该方法不仅具有低内存需求，而且可以并行更新位姿。此外，我们建立了 PieADMM 以 O(1/ϵ²) 的迭代复杂度找到我们模型的 ϵ-驻点解。通过对两个合成数据集和四个 3D SLAM 基准数据集的数值实验，展示了我们所提出算法的效率。

3. 效果展示

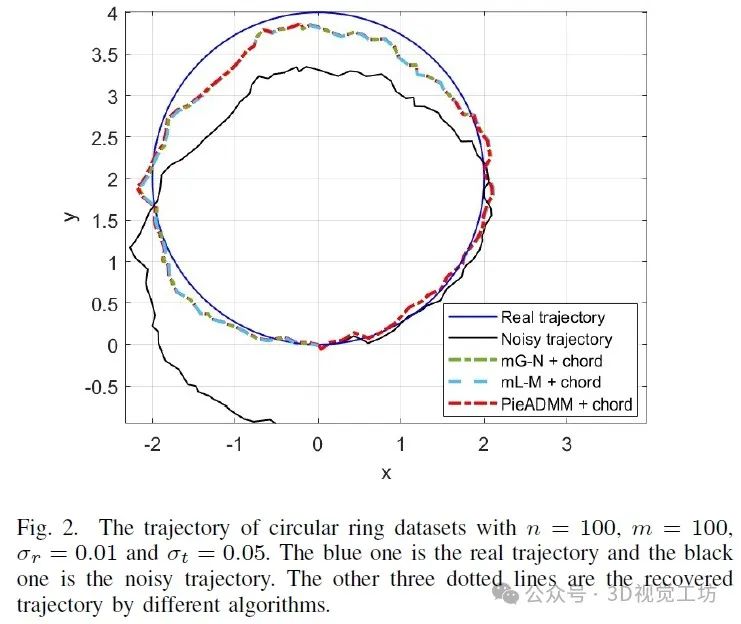
首先，我们使用不同的算法测试n = 100，m = 100的环形数据集。图2显示了当σr = 0.01，σt = 0.05，并采用弦初始化时的俯视轨迹，三种方法在视觉上收敛于相同的解。我们还测试了里程计猜测初始化技术。由于恢复的轨迹几乎重叠，并且很难观察出差异，我们将它们省略了。

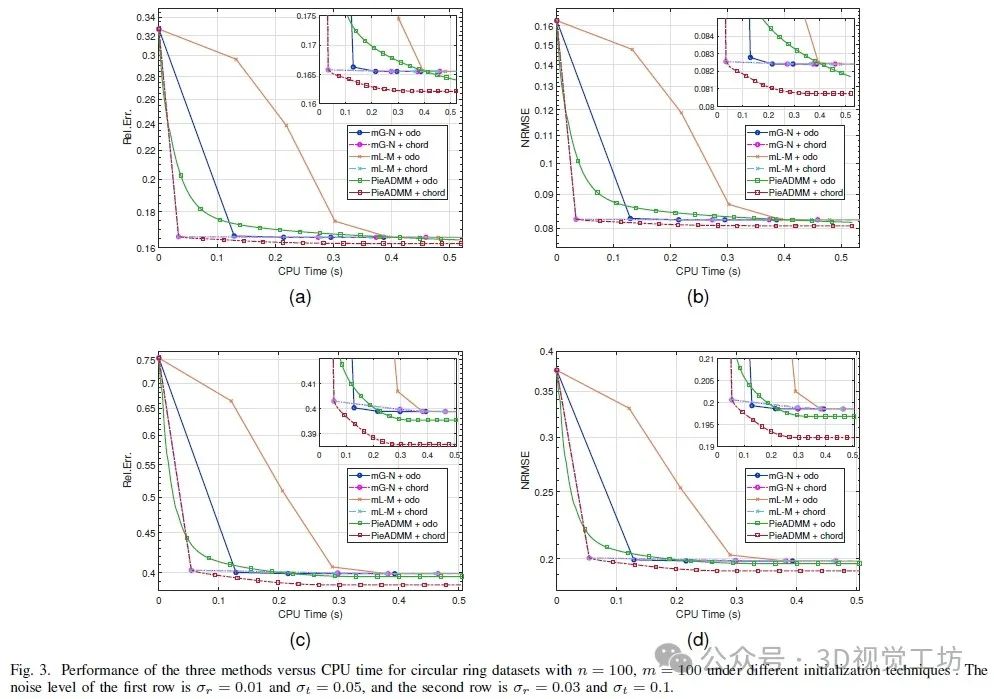
相反，我们在图3中报告了优化过程，记录了在不同方法和初始化技术下，Rel.Err和NRMSE的下降趋势以及CPU时间。由于我们的PieADMM能够针对每个顶点并行更新，因此它可以比其他方法更快地收敛。此外，弦初始化可以在旋转更新后给出平移的估计，这提供了比其他方法更准确的初始点。在此初始化下，我们的PieADMM可以收敛到具有较低相对误差的解。与里程计猜测初始化相比，我们的PieADMM通常不如mG-N的前几步准确，但随着迭代的进行，它可以实现略微更好的性能。因此，我们将弦初始化作为下一步实验中的标准初始化技术。

4. 主要贡献

(i) 我们提出了一种基于增强单位四元数和vMF分布的非凸姿态图优化模型，其中数据存储成本低，单位四元数的投影可以通过归一化计算。

(ii) 我们提出了一种PieADMM，其子问题具有闭式解，并且可以并行更新。

(iii) 基于流形上的一阶最优条件，我们定义了模型的一个ϵ-驻点解。然后，我们建立了PieADMM在找到ϵ-驻点解时的迭代复杂度O(1/ϵ2)。

(iv) 我们在两个不同数据规模的合成数据集和四个三维SLAM基准数据集上测试了我们的算法。数值实验验证了我们方法的有效性。

5. 基本原理是啥？

 

6. 实验结果

我们在额外的噪声水平下比较这些算法，并在表II中列出了关于Rel.Err、NRMSE和CPU时间的数值结果。我们发现PieADMM花费更少的时间并且获得更好的结果。

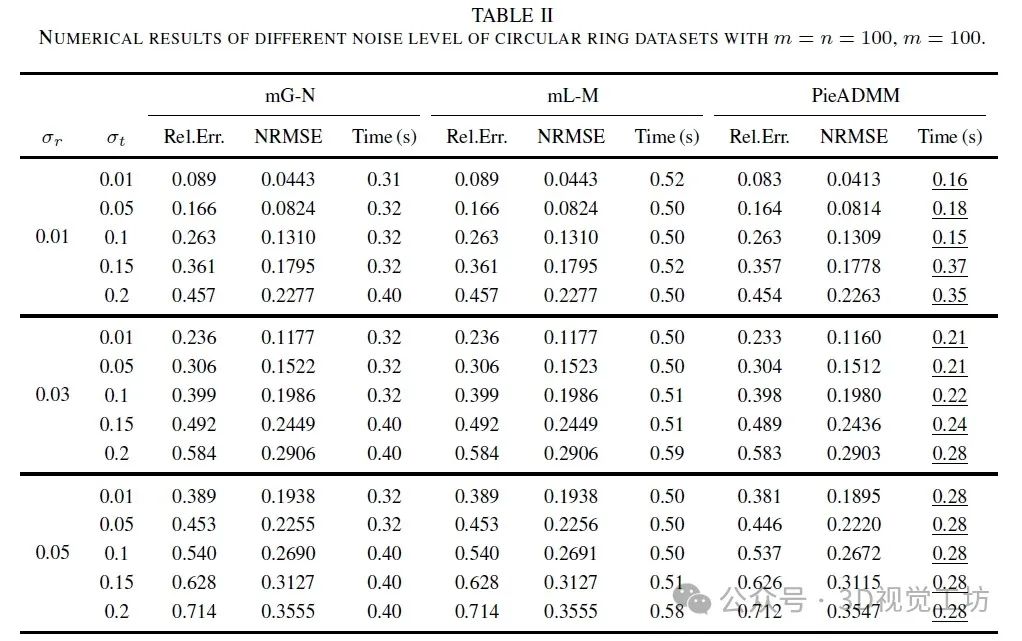
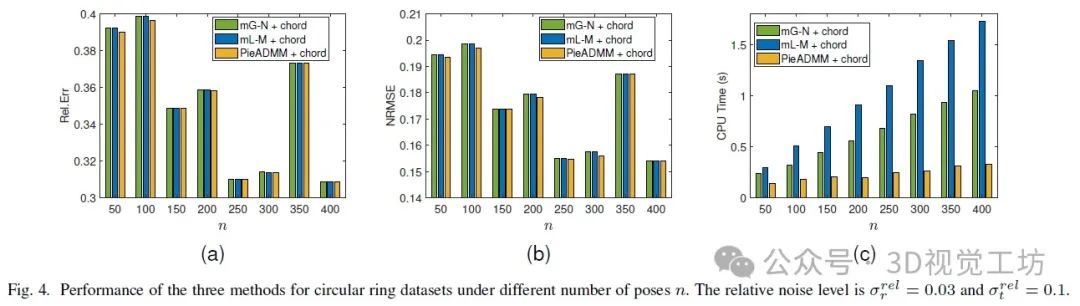
我们还测试了姿态数量n的影响。实际上，由于我们限制了机器人轨迹的范围，同等级别的噪声将在顶点数量增加时产生更大的影响。因此，在比较不同n的数据大小的影响时，我们使用相对噪声水平作为统一标准，这意味着σr = 100 × σrelr / n和σt = 100 × σrelt / n。结果如图4所示。图4a和4b显示了PieADMM的性能平稳，有时略优于其他两种方法。然而，PieADMM的运行时间增加速度比它们慢得多，参见图4c。这是因为n的规模几乎不影响旋转子问题的成本，它可以并行计算。此外，平移子问题仅涉及矩阵乘法，并且不依赖于矩阵的逆。

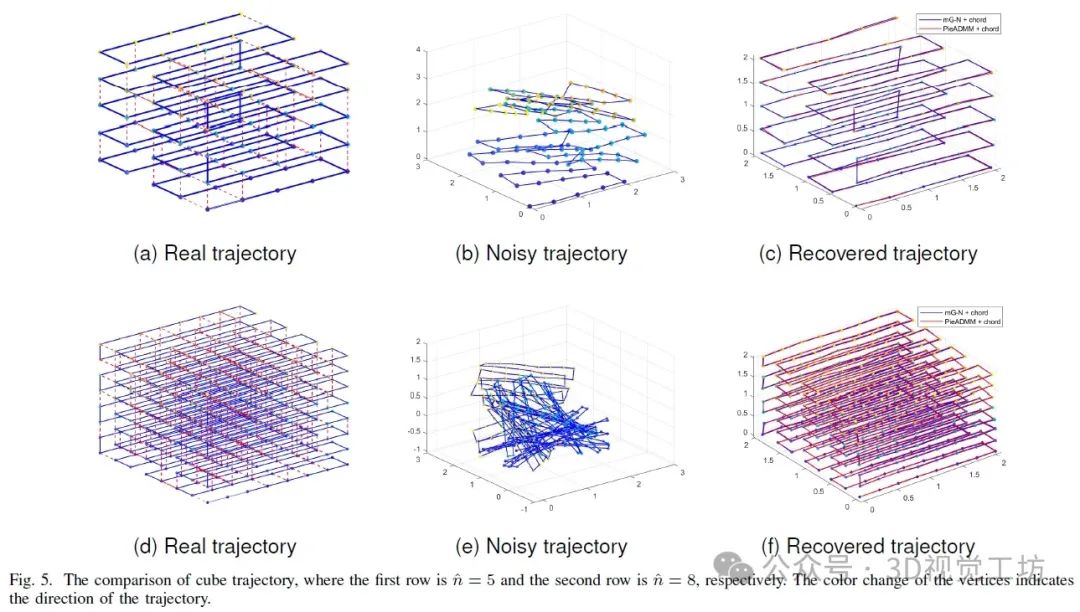
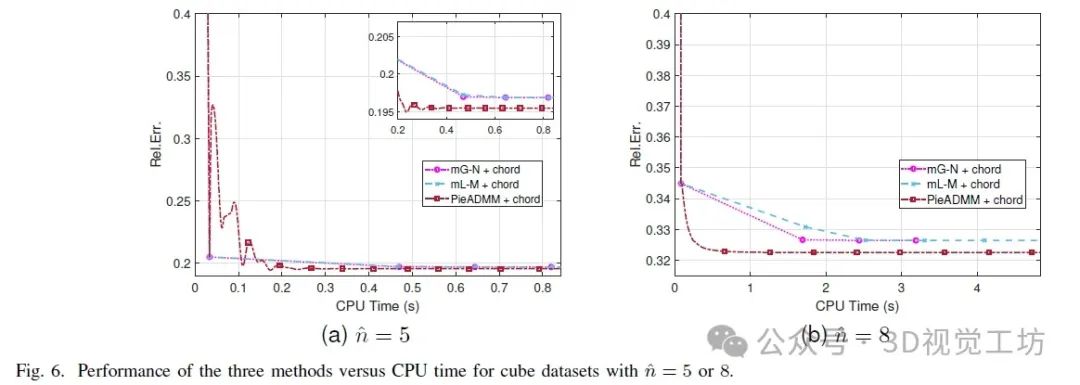
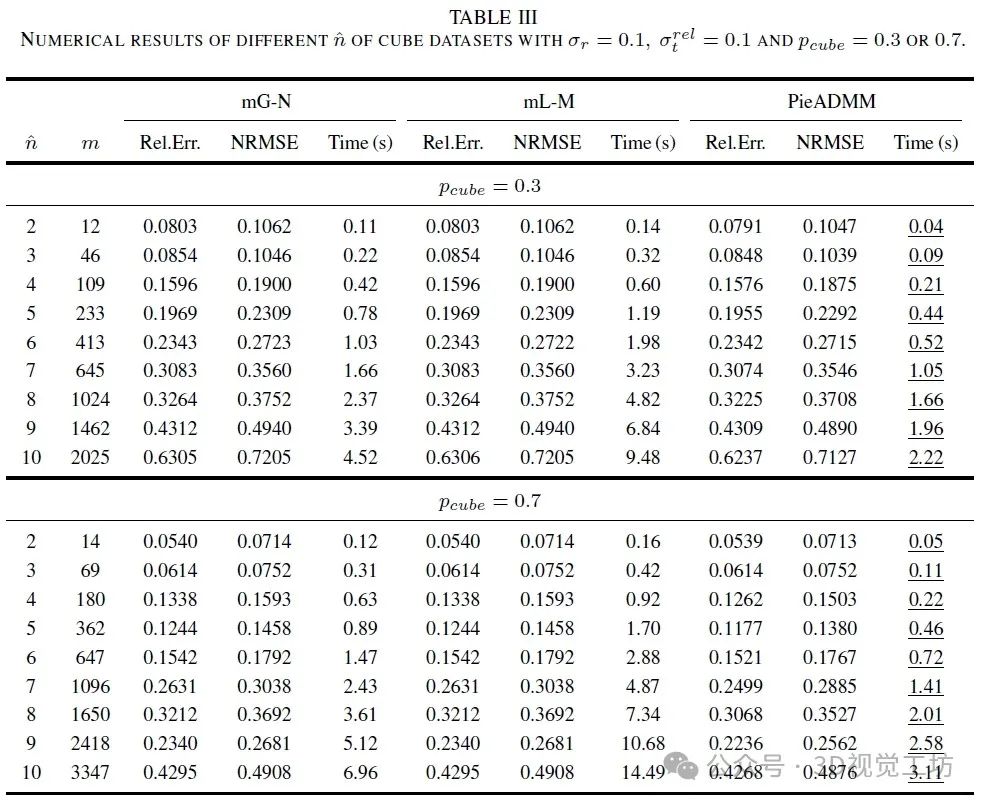
对于立方体数据集，让σt = σrelt /ˆn，其中σrelt表示平移的相对噪声水平。我们首先考虑了ˆn = 5或8，σr = 0.1，σrelt = 0.1和pcube = 0.3的两个例子。图5a和5d显示了真实轨迹，其中蓝线由运动产生，红色虚线由观测产生。图5b、5c和5e、5f分别是对应于不同ˆn的嘈杂和恢复的轨迹。图6显示了Rel.Err随着CPU时间的下降趋势，其中我们省略了图像的上半部分以突出显示细节。由于PGO模型是非凸的，而PieADMM是非单调的算法，曲线可能会振荡。然而，它总是在更短的时间内收敛到更高精度的解。

 

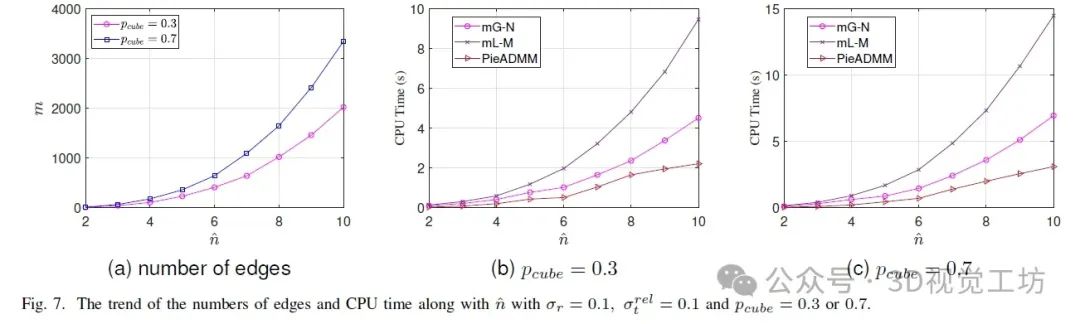
我们还从2到10选择ˆn，并在表III中展示了数值结果。图7a显示了立方体数据集的边缘和顶点数量之间的关系，图7b和7c说明了速度随着ˆn的增加而上升的趋势。mG-N和mL-M的成本增长都是立方的，而PieADMM的增长速度较慢。

 

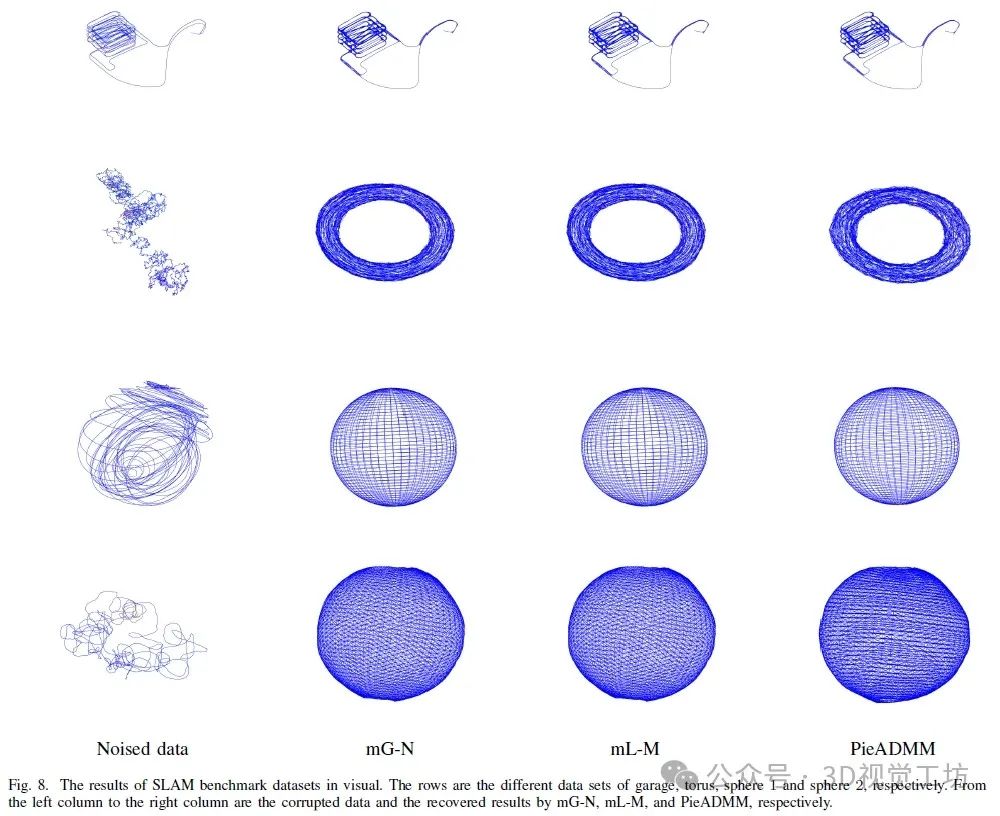
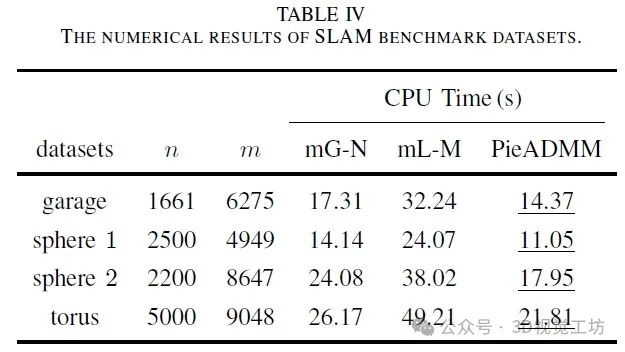
我们测试了一些流行的3D SLAM数据集。车库数据集是一个大规模的真实世界示例，另外三个（球1、球2和环面）是用来比较性能的常见数据集。与球1数据集不同，球2数据集添加了更大的噪声。我们还使用弦初始化技术为所有方法计算了一个初始点。图8显示了轨迹的视觉结果，相应的数值结果列在表IV中。值得注意的是，我们的旋转模型是基于vMF分布而不是传统的高斯分布，因此恢复的解不相同，并且比较目标函数值或梯度是没有意义的。我们在表中显示了CPU时间，表明PieADMM收敛速度比mG-N和mL-M快。

 

7. 总结

在SLAM中的位姿图优化是一种特殊的非凸优化，其中变量通常位于se(3)中，具有非线性目标函数，或在具有正交约束的特殊欧几里得群中。复杂的模型使得找到全局解变得困难。本文提出了一种基于增强单位四元数和冯米塞斯-费舍尔分布的新非凸位姿图优化模型，这是一个在单位球面上的大规模四次多项式优化。通过引入辅助变量，我们将其重新表述为多二次多项式优化、多线性最小二乘问题。然后，我们引入了一个针对PGO模型的近端线性化黎曼ADMM，其中子问题是简单的投影问题，并且可以根据有向图的结构并行解决，从而大大提高了效率。然后，基于我们PGO模型满足的Lipschitz梯度连续性假设和流形上的一阶最优性条件，我们建立了找到ε驻点解的迭代复杂度为O(1/ϵ²)。在两个具有不同数据规模和噪声水平的合成数据集以及四个3D SLAM基准数据集上的数值实验验证了我们方法的有效性。