经典滤波器的设计说明

摘要

经典滤波器的滤波思路是从频率域上将噪声滤掉，关键是设计相应的滤波器传递函数H(s)、H(z)，分别对应着模拟滤波器和数字滤波器的实现。模拟滤波器主要是通过电感(L)、电容(C)、电阻(R)和运放(OPA)等元器件搭建传递函数为H(s)或者近似为H(s)的硬件电路来实现，比如RC滤波电路和有源滤波器等。数字滤波器(DF)从实现的结构上或者是单位脉冲响h(n)上可以分为无限长脉冲响应(IIR)和有限长脉冲响应(FIR)滤波器。两者在结构上的区别是：IIR有反馈回路，即当前输出y(n)中包含以前输出y(n-k)(k>0)；FIR则没有反馈回路，当前输出y(n)中只包含输入x(n)和以前的输入x(n-k)(k>0)。正是有了反馈回路，导致了IIR单位脉冲响应h(n)的无限长。

FIR滤波器

设计流程如下图所示（以窗函数法为例，其它方法不涉及） 

IIR滤波器

设计流程如下图所示（以巴特沃斯低通滤波器采用双线性变换法为例） 

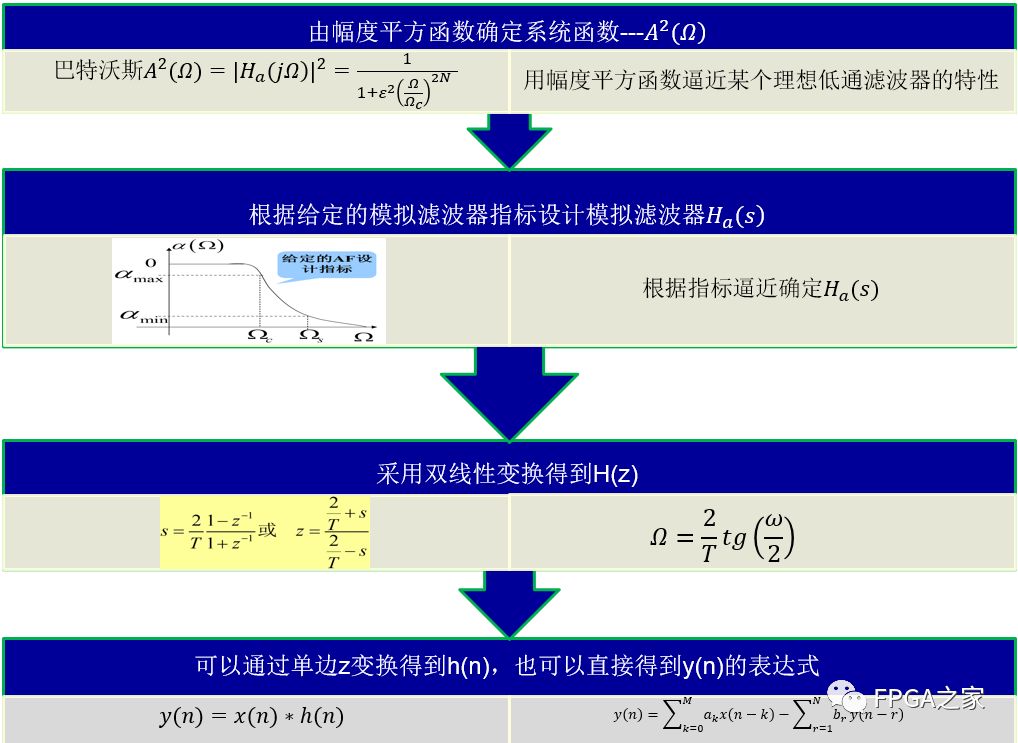
数字滤波器的实现

由上面分析，数字滤波器的两种形式在得到的最后表达式上都可以归一化为N阶线性常系数差分方程的一般形式： 

y(n)=∑Mk=0akx(n−k)−∑Nr=1bry(n−r)

这样一个系统的实现可以分别从硬件和软件上实现：硬件上只需要包括移位寄存器、乘法器和加法器就可以；软件上实现就较为简单了，直接高级语言描述。

两种经典数字滤波器的比较

如下图所示： 

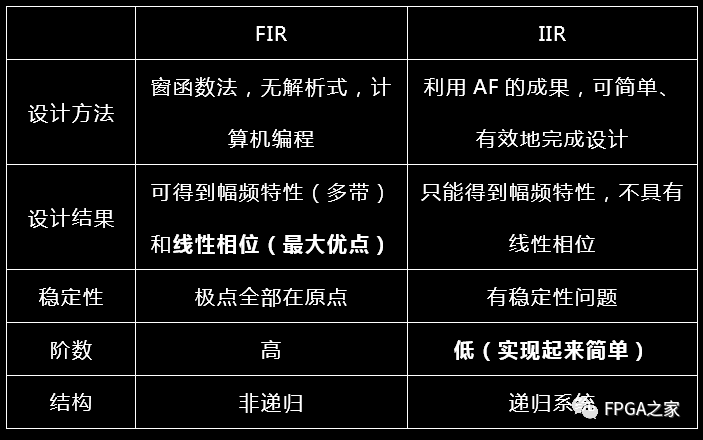
基于Matlab的实验

用窗函数法设计FIR数字滤波器

设计一线性相位低通FIR数字滤波器，通带截止频率wp=0.2π ，通带最大衰减0.25dB，阻带起始频率ws=0.3π ，阻带最小衰减50dB。请给出N和所选窗函数，求出h(n)，并绘制相应的幅频特性（dB）曲线，根据该图给出实际的阻带衰减，绘制窗函数的时域频域特性曲线。

实验过程分析： 
阻带最小衰减为50dB，对于各种窗函数的基本参数，不能用矩形窗和汉宁窗函数，因为它们的阻带最小衰减不能满足设计的要求，因此可以选用汉明和布莱克曼窗进行FIR数字滤波器的设计。为了对比汉宁窗不能满足设计要求，同样做出汉宁窗设计的FIR数字滤波器。 
根据通带截止频率和阻带起始频率得到过渡带的带宽，汉明窗对应的数字滤波器的过渡带宽为8π÷N，推出用汉明窗设计时的数字滤波器的至少N=80，为了取用类型I，即偶对称、N为奇数，取用N=81；对于用布莱克曼窗对应的数字滤波器的过渡带宽为12π÷N，推出N=120，取N=121。汉宁窗与汉明窗的N值计算相同。 
首先给出汉明窗的FIR实验结果： 

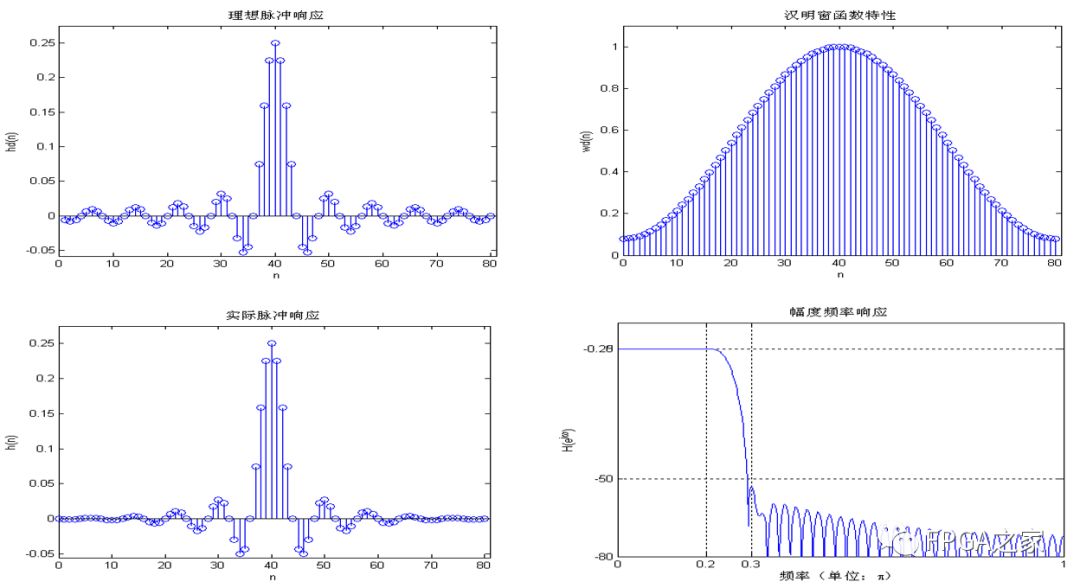
察汉明窗设计的FIR滤波器的幅频特性曲线，在通带内，最大衰减小于0.25db，在阻带内，最小衰减大于50db，满足了设计要求。 
然后给出布莱克曼窗的FIR实验结果： 

 
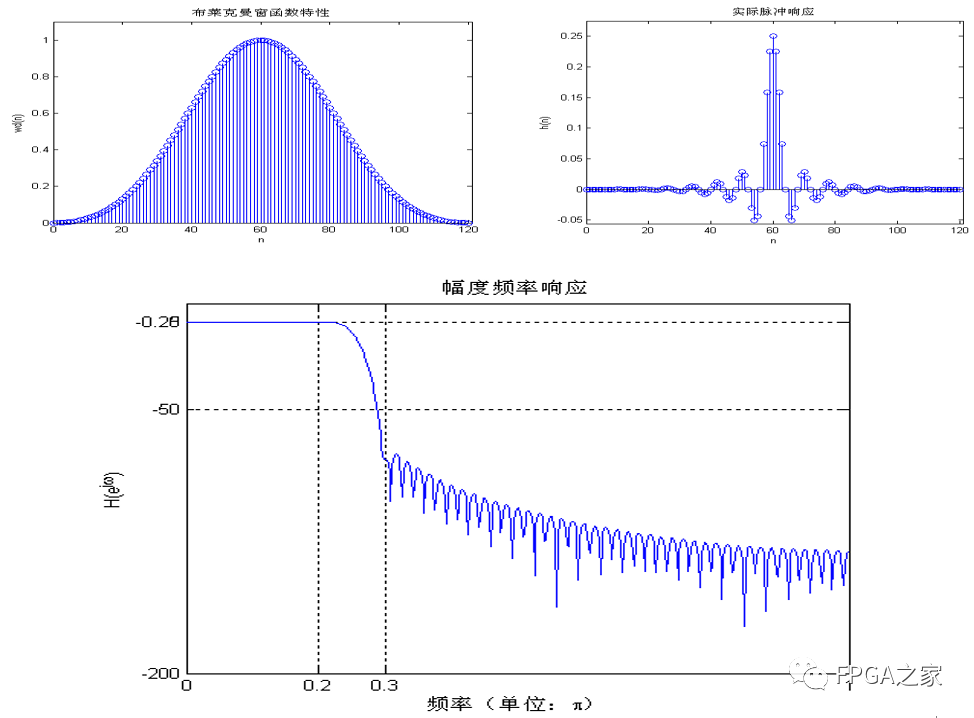
观察布莱克曼窗设计的FIR滤波器的幅频特性曲线，在通带内，最大衰减小于0.25db，在阻带内，最小衰减大于50db，满足了设计要求。 
最后给出汉宁窗的FIR实验结果作为对比： 

 
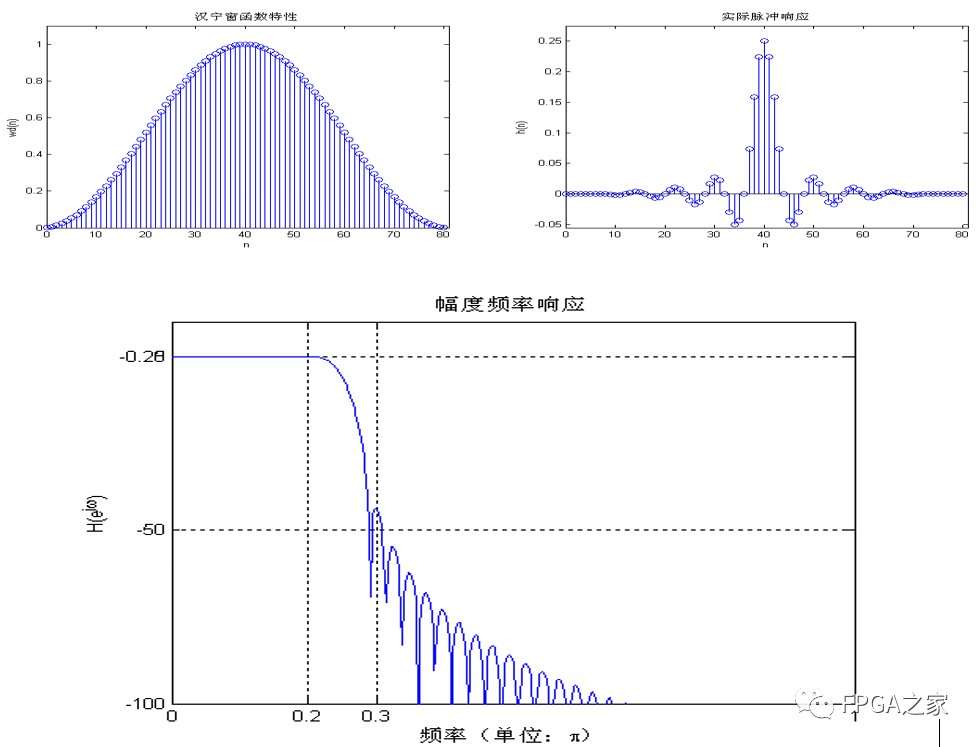
观察汉宁窗设计的FIR滤波器的幅频特性曲线，在通带内，最大衰减小于0.25db，但在阻带内最小衰减小于了50db，所以不满足设计要求。

一般地，随着N值增大，过渡带愈加陡峭，衰减更快。旁瓣越多对应的通带起伏越大。为了获得更加平稳的通带和更加陡峭的过渡带，虽然不能兼得，一般处理时是通过增加主瓣宽度来换取对旁瓣的抑制。

用双线性变换法设计IIR数字滤波器

用双线性变换法设计一个IIR巴特沃斯低通数字滤波器。设计指标参数为：在通带内频率低于0.2π 时，最大衰减小于1dB；在阻带内[0.3π,π] 频率区间上，最小衰减大于15dB。用所设计的滤波器对实际心电图信号采样序列进行仿真滤波处理，并分别绘出滤波前后的心电图信号波形图。观察总结滤波作用与效果。

实验结果： 

 

 

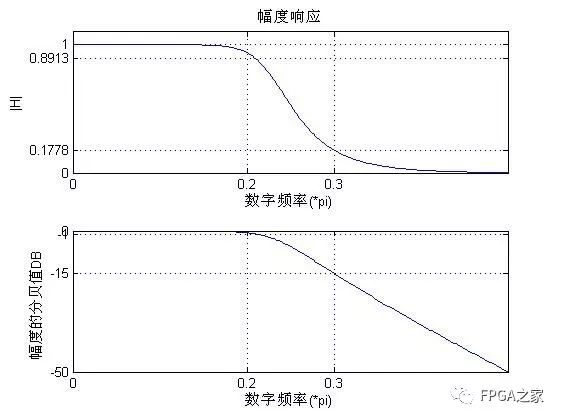
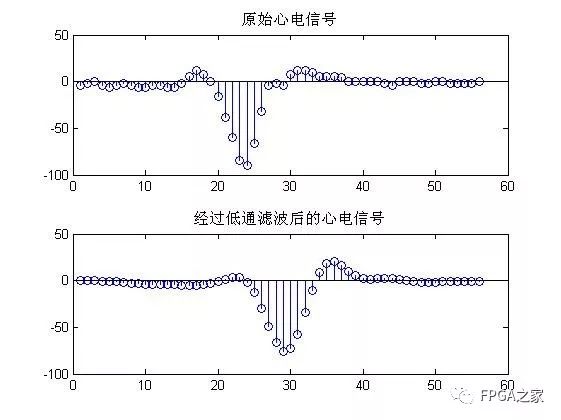
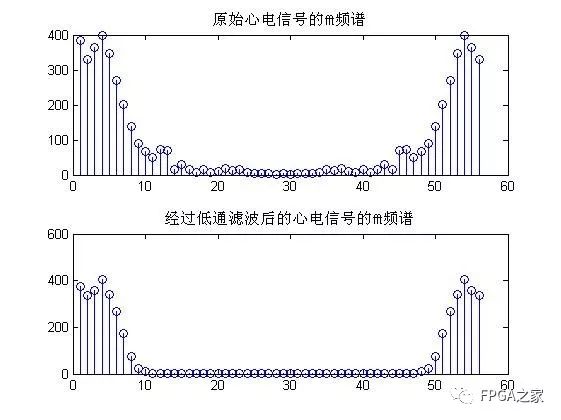
实验结果分析： 
由幅频特性曲线可以看出设计的IIR滤波器满足要求，同时经过心电信号的测试，能够达到滤除高频噪声的目的。 
本实验中，经IIR设计的滤波器传递函数H(z)为： 

 
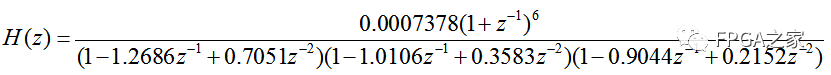
计算得到一般的线性系统表达式： 

y(n)=0.0007378x(n)+0.004427x(n−1)+0.01107x(n−2)+0.01476x(n−3)+0.01107x(n−4)+0.004427x(n−5)+0.0007378x(n−6)+3.184y(n−1)−4.622y(n−2)+3.779y(n−3)−1.814y(n−4)+0.48y(n−5)−0.05445y(n−6)

一般设计滤波器就是为了得到上面的表达式，有了这样的表达式之后就可以很方便的通过硬件或者软件实现滤波器了。

Matlab代码

FIR滤波器

理想低通滤波器的构建：

 

 

function hd= ideal_lp( wc,N )
%hd=点0到N-1之间的理想脉冲响应
% wc=截止频率（弧度）
%N=滤波器的长度
tao=(N-1)/2;
n=[0:(N-1)];
%+eps转换成浮点数
m=n-tao+eps;
hd=sin(wc*m)./(pi*m);
end

 

 

布莱克曼窗FIR滤波器：

 

 

%阻带最小衰减为50DB，所以可以选择汉明窗
wp=0.2*pi;ws=0.3*pi;
deltaw=ws-wp;%过渡带宽
N0=12*pi/deltaw;
%N0=ceil(6.6*pi/deltaw);
N=N0+mod(N0+1,2);%为实现FIR类型I偶对称滤波器，确保N为奇数。
windows=(blackman(N))';
wc=(ws+wp)/2;
hd=ideal_lp(wc,N);
b=hd.*windows;
[H,w]=freqz(b,1);
n=0:N-1;
dw=2*pi/100;
dbH=20*log10((abs(H)+eps)/max(abs(H)));%化为分贝值
%Rp=-(min(db(1:wp/dw+1)))%检验通带波动
%As=-round(max(db(ws/dw+1:501)))%检验最小阻带衰减
%作图
subplot(221)
stem(n,hd);
axis([0,N,1.1*min(hd),1.1*max(hd)]);title('理想脉冲响应');
xlabel('n');
ylabel('hd(n)');
subplot(222);
stem(n,windows);
axis([0,N,0,1.1]);
title('布莱克曼窗函数特性');
xlabel('n');
ylabel('wd(n)');
subplot(223),stem(n,b);
axis([0,N,1.1*min(b),1.1*max(b)]);title('实际脉冲响应');
xlabel('n');
ylabel('h(n)');
subplot(224);
plot(w/pi,dbH);
title('幅度频率响应');
axis([0,1,-200,10]);
xlabel('频率（单位：pi）');
ylabel('H(e^{jomega})');
set(gca,'XTickMode','manual','XTick',[0,wp/pi,ws/pi,1]);
set(gca,'YTickMode','manual','YTick',[-200,-50,-0.25,0]);
grid

 

 

汉明窗FIR滤波器：

 

 

%阻带最小衰减为50DB，所以可以选择汉明窗
wp=0.2*pi;ws=0.3*pi;
deltaw=ws-wp;%过渡带宽
N0=8*pi/deltaw;
%N0=ceil(6.6*pi/deltaw);
N=N0+mod(N0+1,2);%为实现FIR类型I偶对称滤波器，确保N为奇数。
windows=(hamming(N))';
%windows=ones(1,N);
wc=(ws+wp)/2;
hd=ideal_lp(wc,N);
b=hd.*windows;
[H,w]=freqz(b,1);
n=0:N-1;
dw=2*pi/100;
dbH=20*log10((abs(H)+eps)/max(abs(H)));%化为分贝值
%Rp=-(min(db(1:wp/dw+1)))%检验通带波动
%As=-round(max(db(ws/dw+1:501)))%检验最小阻带衰减
%作图
figure(1)
%subplot(221)
stem(n,hd);
axis([0,N,1.1*min(hd),1.1*max(hd)]);title('理想脉冲响应');
xlabel('n');
ylabel('hd(n)');
figure(2)
%subplot(222);
stem(n,windows);
axis([0,N,0,1.1]);
title('汉明窗函数特性');
xlabel('n');
ylabel('wd(n)');
figure(3)
%subplot(223),
stem(n,b);
axis([0,N,1.1*min(b),1.1*max(b)]);title('实际脉冲响应');
xlabel('n');
ylabel('h(n)');
figure(4)
%subplot(224);
plot(w/pi,dbH);
title('幅度频率响应');
axis([0,1,-80,10]);
xlabel('频率（单位：pi）');
ylabel('H(e^{jomega})');
set(gca,'XTickMode','manual','XTick',[0,wp/pi,ws/pi,1]);
set(gca,'YTickMode','manual','YTick',[-80,-50,-0.25,0]);
grid

 

 

汉宁窗FIR滤波器：

 

 

%阻带最小衰减为50DB，所以可以选择汉明窗
wp=0.2*pi;ws=0.3*pi;
deltaw=ws-wp;%过渡带宽
N0=8*pi/deltaw;
%N0=ceil(6.6*pi/deltaw);
N=N0+mod(N0+1,2);%为实现FIR类型I偶对称滤波器，确保N为奇数。
windows=(hanning(N))';
wc=(ws+wp)/2;
%计算得到理想低通滤波器，已经移位（N-1）/2
hd=ideal_lp(wc,N);
%加窗施加在hn上
b=hd.*windows;
%
[H,w]=freqz(b,1);

n=0:N-1;
dw=2*pi/100;
dbH=20*log10((abs(H)+eps)/max(abs(H)));%化为分贝值
%Rp=-(min(db(1:wp/dw+1)))%检验通带波动
%As=-round(max(db(ws/dw+1:501)))%检验最小阻带衰减
%作图
subplot(221)
stem(n,hd);
axis([0,N,1.1*min(hd),1.1*max(hd)]);title('理想脉冲响应');
xlabel('n');
ylabel('hd(n)');
subplot(222);
stem(n,windows);
axis([0,N,0,1.1]);
title('汉宁窗函数特性');
xlabel('n');
ylabel('wd(n)');
subplot(223),stem(n,b);
axis([0,N,1.1*min(b),1.1*max(b)]);title('实际脉冲响应');
xlabel('n');
ylabel('h(n)');
subplot(224);
plot(w/pi,dbH);
title('幅度频率响应');
axis([0,1,-100,10]);
xlabel('频率（单位：pi）');
ylabel('H(e^{jomega})');
set(gca,'XTickMode','manual','XTick',[0,wp/pi,ws/pi,1]);
set(gca,'YTickMode','manual','YTick',[-100,-50,-0.25,0]);
grid

 

 

IIR数字滤波器

IIR滤波器设计：

 

 

%双线性变换前预畸
Fs=500;
wp=(100/Fs)*2*pi;
ws=(200/Fs)*2*pi;
Rp=2;
Rs=15;
wp2=2*Fs*tan(wp/2);
ws2=2*Fs*tan(ws/2);
%选择滤波器的最小阶数
[N,wn]=buttord(wp2,ws2,Rp,Rs,'s');%注意此处输入的是畸变后的指标，输出N为符合要求的模拟滤波器的最小阶数，wn为3dB带宽
%创建butterworth模拟滤波器
[Z,P,K]=buttap(N);
%把滤波器零极点模型转化为传递函数模型
[Bap,Aap]=zp2tf(Z,P,K);
%把模拟滤波器原型转换为截止频率为wn的模拟低通滤波器
[b,a]=lp2lp(Bap,Aap,wn);
%用双线性法实现模拟滤波器到数字滤波器的转换
[bz,az]=bilinear(b,a,Fs);
%绘制频率响应曲线
[H,W]=freqz(bz,az);
subplot(2,1,1);
plot(W/pi,abs(H));
grid;
xlabel('频率w/pi');
ylabel('幅度绝对值');
subplot(2,1,2);
plot(W/pi,20*log10((abs(H)+eps)/max(abs(H))));
grid;
xlabel('频率w/pi');
ylabel('幅度dB');

 

 

心电信号滤波：

 

 

%数字滤波器指标：
wc=0.2*pi;ws=0.3*pi;Rp=1;As=15;
ripple=10^(-Rp/20);Attn=10^(-As/20);
%转换成为模拟指标：
Fs=1;T=1/Fs;
Omgp=(2/T)*tan(wc/2);
Omgs=(2/T)*tan(ws/2);
%模拟原型滤波器计算：
[n,Omgc]=buttord(Omgp,Omgs,Rp,As,'s');%计算阶数和截止频率
[z0,p0,k0]=buttap(n);
ba=k0*real(poly(z0));
aa=real(poly(p0));
[ba1,aa1]=lp2lp(ba,aa,Omgc);
%双线性变换法计算数字滤波器系数
[bd,ad]=bilinear(ba1,aa1,Fs);%双线性变换法求数字滤波器系数b,a
tf(bd,ad,1)
[sos,g]=tf2sos(bd,ad)%由直接型转变成级联型
%求数字系统的频率特性:
[H,w]=freqz(bd,ad);
dbH=20*log10((abs(H)+eps)/max(abs(H)));%化为分贝值
subplot(2,1,1);
plot(w/pi,abs(H));
% 加上对应取值轴来验证是否满足设计要求
set(gca,'XTickMode','Manual','XTick',[0,0.2,0.3,pi])
set(gca,'YTickMode','Manual','YTick',[0,Attn,ripple,1])
ylabel('|H|');
xlabel('数字频率(*pi)')
title('幅度响应');
axis([0,1/2,0,1.1]);
grid on
subplot(212);
plot(w/pi,dbH);
xlabel('数字频率(*pi)');
ylabel('幅度的分贝值DB');
% 加上对应取值轴来验证是否满足设计要求
set(gca,'XTickMode','Manual','XTick',[0,0.2,0.3,pi])
set(gca,'YTickMode','Manual','YTick',[-50,-As,-Rp,0])
axis([0,1/2,-50,0.1]);
grid on

%心电信号：
xn=[-4,-2,0,-4,-6,-4,-2,-4,-6,-6,-4,-4,-6,-6,-2,6,12,8,...
    0,-16,-38,-60,-84,-90,-66,-32,-4,-2,-4,8,12,12,10,6,...
    6,6,4,0,0,0,0,0,-2,-4,0,0,0,-2,-2,0,0,-2,-2,-2,-2,0]
figure;
subplot(211);
stem(xn);
title('原始心电信号')
yn=filter(bd,ad,xn);

subplot(212);
stem(yn);
title('经过低通滤波后的心电信号')

figure;
subplot(211);
stem(abs(fft(xn)));
title('原始心电信号的fft频谱')
yn=filter(bd,ad,xn);
subplot(212);
stem(abs(fft(yn)));

 

 

title('经过低通滤波后的心电信号的fft频谱');