使用CUDA-Q实现量子聚类算法

量子计算机能够利用叠加、纠缠和干涉等量子特性，从数据中归纳出知识点并获得洞察。这些量子机器学习（QML）技术最终将在量子加速的超级计算机上运行，这种超级计算机结合了 CPU、GPU 和 QPU 的处理能力，能够解决一些世界上最复杂的难题。

许多 QML 算法都假定经典数据可以通过使用所谓的量子随机存取存储器（QRAM）进行叠加来实现高效加载，由此提供理论上的加速。由于缺乏实现 QRAM 的有效方法，早期的量子计算机将很有可能只擅长计算，而非数据密集型任务。

实际上，在近期和中期的硬件端上有效运行的 QML 算法必须侧重于计算密集型启发式方法，以便于在没有 QRAM 的情况下分析数据。

本文将重点介绍爱丁堡大学信息学院量子软件实验室副教授 Petros Wallden 博士及其团队的最新研究成果。Petros 是量子信息学领域的专家，研究范围涵盖量子算法、量子密码学、量子信息学基础等方面。 

Petros 的团队使用 NVIDIA CUDA-Q（其前身为 CUDA Quantum）平台开发和加速新 QML 方法的模拟，显著减少了研究大型数据集所需的量子比特数。

麻省理工学院（MIT）物理学家 Aram Harrow 的研究利用了核心集的概念，为 QML 应用提供了一种新颖的方法，无需 QRAM 就能为其构建现实可行的预言机（oracle）。Petros 的团队对这一研究进行了扩展。

什么是核心集？

核心集（coreset）是通过提取完整数据集并将其优化映射到较小的加权数据集而形成的（图 1）。然后，就可以对核心集进行分析，在无需直接处理完整数据集的情况下，近似表示完整数据集的特征。

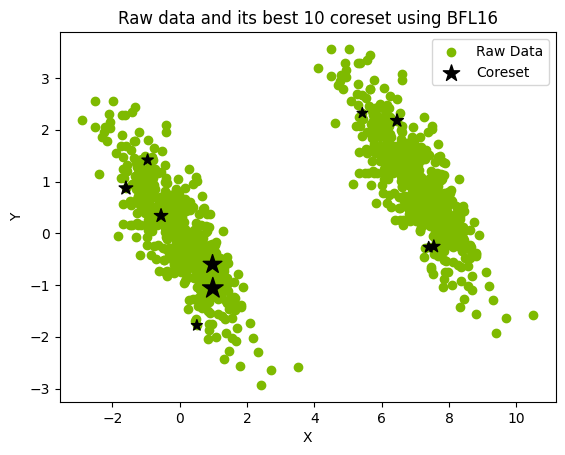
图 1.用大小为 10 的核心集表示 1000 个点的数据集

核心集是在聚类应用之前采用对数据进行预处理的经典降维方法所产生的结果。通过采用核心集，数据密集型 QML 任务就可以用数量级较少的量子比特来近似表示，并使其成为更加接近实际的近期量子计算应用。

标准的经典核心集构建技术通常先从数据集和目标误差开始，然后确定核心集的最佳大小，以满足误差要求。由于实验限制，Petros 的团队根据可用量子比特的数量来选择核心集的大小，然后在量子计算后评估了这一选择产生的误差。

使用核心集进行聚类的量子方法

在将输入数据缩小到可控大小的核心集后，Petros 的团队得以探索三种量子聚类算法。

聚类（Clustering）是一种无监督学习方法，该技术描述了一系列以有意义的方式对相似数据点进行分组的方法。这些分组或集群可用于在现实世界的应用中作出明智的决策，例如确定肿瘤是恶性还是良性。

Petros 的团队使用 CUDA-Q 实现了以下聚类技术：

分裂聚类

在该方法中，核心集数据点从一个集群开始，依次进行双分区，直到每个数据点都在自己的集群中。该方法可以在第 K 次迭代时停止进程，以便查看数据是如何被划分到 K 个集群中（图 2）。

三均值聚类

根据每个数据点与 K 个不断演化的质量中心（质心）的关系，将数据点划分到 K 个集群（本例中为 3 个）。当三个集群会聚并且不再随新的迭代而变化时，过程结束。

高斯混合模型（GMM）聚类

潜在核心点位置的分布被表示为 K 个高斯分布的混合。根据每个核心点最有可能来自哪个高斯分布，将数据分类到 K 个集。

每种聚类技术都会输出一组核心集，以及原始数据集中的每个点到这些核心集之一的映射。其结果是初始大型数据集的近似聚类和降维。

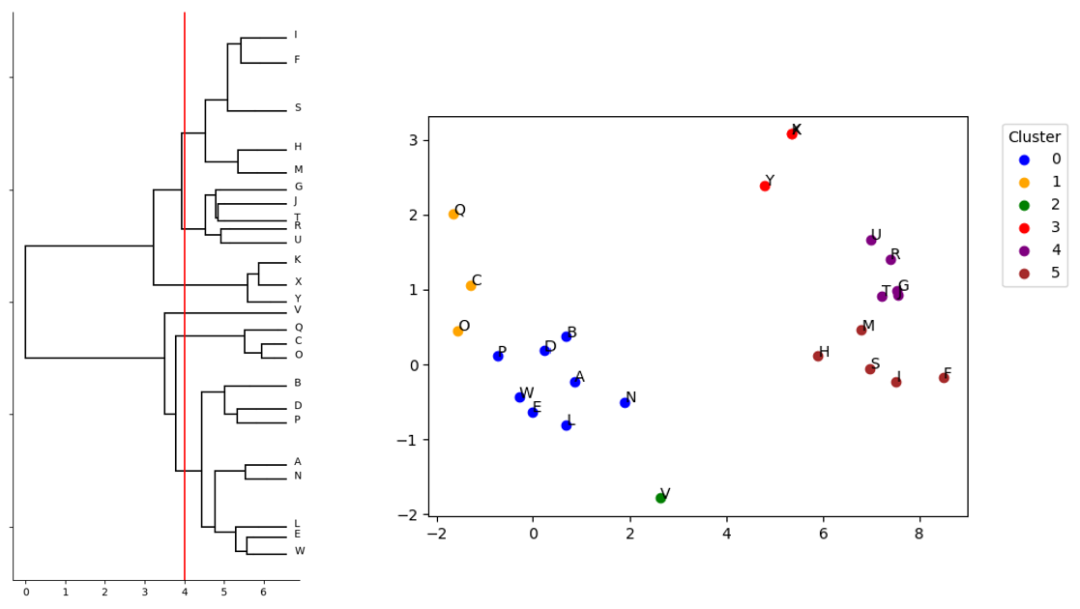
图 2.N=25 核心集 QML 分裂聚类模拟结果

通过使用变分量子算法（VQA）框架，每种技术都能以使用 QPU 的方式表达。Petros 和其团队通过推导出一个加权量子比特哈密顿量（受最大切割问题的启发），为上述每种聚类方法各自的成本函数进行了编码，从而实现了这一目标。有了这样一个哈密顿量，VQA 迭代过程就能反复调用真实或模拟的 QPU，从而高效计算每个聚类例程所需的成本最小化。

使用 CUDA-Q 克服可扩展性挑战

为了探究这些 QML 聚类方法的有效性，就需要对每种算法的性能表现进行模拟。

NVIDIA CUDA-Q 模拟套件可对每种聚类方法进行全面模拟，可处理的最大问题规模为 25 个量子比特。CUDA-Q 通过实现对 GPU 硬件的便捷访问，加快了这些模拟的速度。其还提供开箱即用的原语，例如用于将基于哈密顿量的优化过程参数化的硬件高效 ansatz 内核，以及可轻松适应聚类算法成本函数的自旋哈密顿量等。

事实上，只有通过 CUDA-Q 提供的 GPU 加速，才能实现 Petros 团队在其论文《在小型量子计算机上的大数据应用》中提出的模拟规模。

最初的实验只在 CPU 硬件上模拟了 10 个量子比特，但由于内存限制，无法进行 25 个量子比特规模的实验。通过 CUDA-Q，最初的 10 个量子比特的模拟代码实现了即时兼容性，因此当 Petros 的团队需要将 CPU 硬件换成 NVIDIA DGX H100 GPU 系统时，无需修改即可运行。

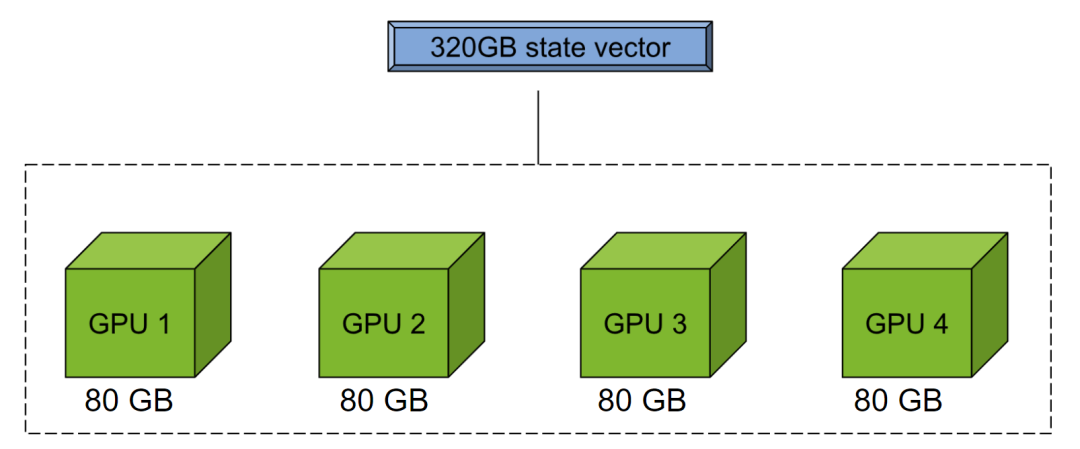
图 3.CUDA-Q mgpu 后端通过池化多个 GPU 的内存执行大型状态向量模拟

这种代码可扩展性是一个巨大的优势。由于可以使用 NVIDIA mgpu 后端池化多个 GPU 的内存（图 3），Petros 和其团队后来在同样无需大幅修改原始模拟代码的情况下，通过改变后端目标进一步扩大了模拟规模。

这项研究的主要开发者 Boniface Yogendran 表示：“有了 CUDA-Q，我们就不必担心量子比特可扩展性方面的限制，从研究开始的第一天起就已经为实现高性能计算做足了准备。”

由于 CUDA-Q 本身也支持 QPU，Yogendran 的代码可以将这项工作扩展到模拟以外，为所有主要 QPU 模态上的部署提供支持。

CUDA-Q 模拟的价值

由于能够轻松模拟所有三种聚类算法，Petros 与其团队得以将每种算法与用于寻找全局最优解的蛮力方法（用于寻找全局最优解）和一种名为劳埃德算法（Lloyd’s algorithm）的经典启发式方法进行比较。结果表明，量子算法在 GMM（K=2）方面表现最佳，而分裂聚类方法则与劳埃德算法不相上下。

基于这项工作的成功，Petros 的团队计划继续与 NVIDIA 合作，利用 CUDA-Q 继续开发和扩展新的量子加速超级计算应用。

探索 CUDA-Q

CUDA-Q 使 Petros 和他的团队能够便捷地开发出新颖的 QML 实现方法，并利用加速计算对其进行模拟。通过使用 CUDA-Q，可使代码具有可移植性，以便进一步进行大规模模拟或在物理 QPU 上部署。

了解有关 CUDA-Q 量子的更多信息或马上开始使用，请参见分裂聚类 Jupyter 笔记本，其中探讨了本文中描述的核心集赋能的分裂聚类方法。该教程展示了如何使用 GPU 便捷扩展代码并运行 34 个量子比特的实例。