半导体的能带理论

本文较为详细地介绍半导体的能带理论。  

半导体能带理论及结构

半导体技术的持续发展得益于半导体理论在固体电子学(随着固体器件特别是半导体集成电路的空前发展出现的一门新兴学科)基础上的建立与发展，其主要内容可概括为研究半导体中载流子(carrier)按能量状态的分布、跃迁(能量状态的改变)和输运(能量的定向传递)。   本文会向大家较为详细地介绍半导体能带理论。   对于物质划分为导体、半导体和绝缘体，主要依据是其电子状态。   能带理论：描述固体中电子按能量分布的状态，从而对导体、半导体和绝缘体从本质上做出科学区分的理论。   能带理论的基本观点认为任何固体中所有电子的能级并非按能量均匀分布，而是在某一能量范围内密集成带，而与其邻接的高、低两个能量范围却是电子的能量禁区；或者说固体中所有电子的允许能级皆按其所属电子性质的不同而密集成不同的能带，能带之间由称为禁带或能隙的能量禁区隔开。  

电子的波粒二象性

电子的波粒二象性是近代电子论从理论和实验两方面证明的，其内涵是指电子及其运动既有粒子性特征，也有波动性特征。通常用德布罗意关系来描述电子波粒二象性，其数学表达式如下:   P=hk，E=hv   式中，k为波的特征参数波矢k，v为频率，P，E分别对应动量和能量，h为普朗克常数。  2.自由空间中的电子和周期势场中的电子  根据经典力学中运动粒子能量与动量的关系和上述德布罗意关系，可将自由空间中电子能量与动量的关系表示为能量与波数(波矢)的关系:   E(k)=(hk)^2/2m   这是一个抛物线型的以波数k为自变量的连续函数，式中m为电子性质量。   考虑单个电子在一维周期势场来概括固体中电子的运动环境，据此求解电子波函数的薛定谔方程，建立了能带理论的基本构架。结果表明，在一维周期势场中，受周期势场的扰动，电子的E(k)函数在=±nπ/2a，n=1,2,3…处不连续、如下图（图1）所示：  

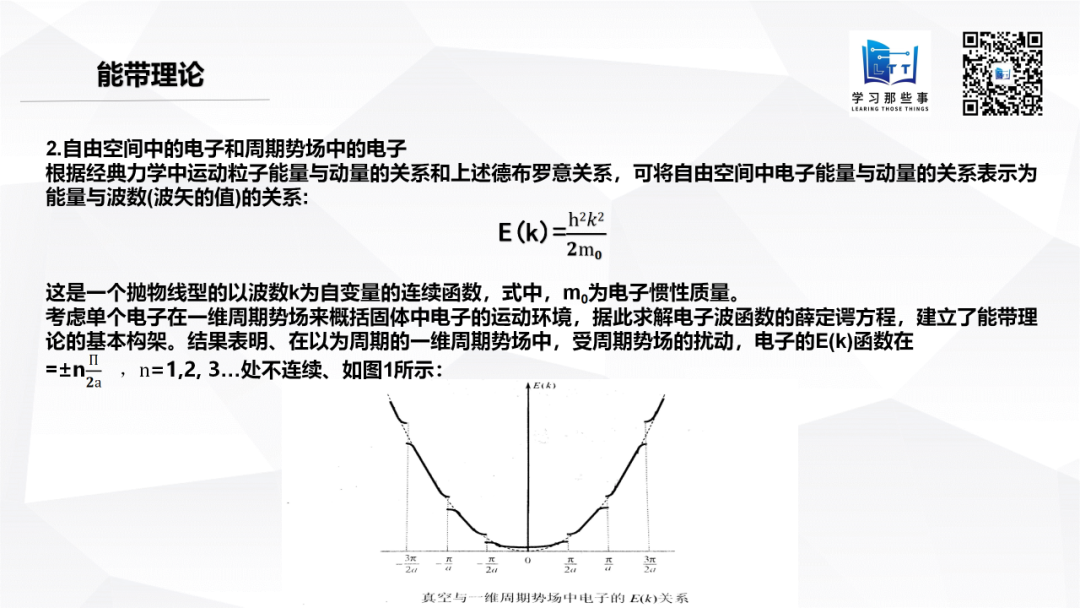
图1 真空与一维周期势场中电子的E(k)关系   所谓能带结构，就是固体中电子的能量与动量之间的关系，即函数E(k)。不涉及电子的动量变化，只是能带结构的一种简易表示法，如下图（图2）所示：  

  晶体中出现一个由N条分裂能级构成的s能带，其N个价电子只能填满下面一半能级，如(a)所示；绝对零度时，其4N个价电子恰好填满能量较低的一个能带(成键带)，能量较高的能带(反键带)空着，如(b)所示；当原子因为有8个外层电子，其所有分裂能级都会被电子填满，不会出现空状态，如(c)所示。   而图1，可以看做是一个理想一维晶体的E(k)关系。对于实际的三维晶体，其E(k)关系显然要复杂得多。为了清晰反映某种材料能带结构的主要特征，通常只在动量空间的两个特征方向[譬如(100)方向和(111)方向]上画出E(k)函数曲线。所谓主要特征，就是导带E(k)函数的极小值和价带E(k)函数的极大值。重点关注这些极值能量的高低、在k空间出现的位置以及极值处曲线的曲率。   综上所述：固体中电子状态之所以符合能带理论这一特征既与电子的本性(即电子的波粒二象性)有关，也与固体这一电子所处的环境(即原子周期排列形成原子核对电子的周期性势场)有关。   在图1中，虚线表示真空中电子的E(k)关系，实线表示周期势场中电子的E(k)关系，是一个理想一维晶体的E(k)关系。而实际的三维晶体，其E(k)关系会复杂得多。   下图分别是锗、硅和砷化镓三种半导体的能带结构图：  

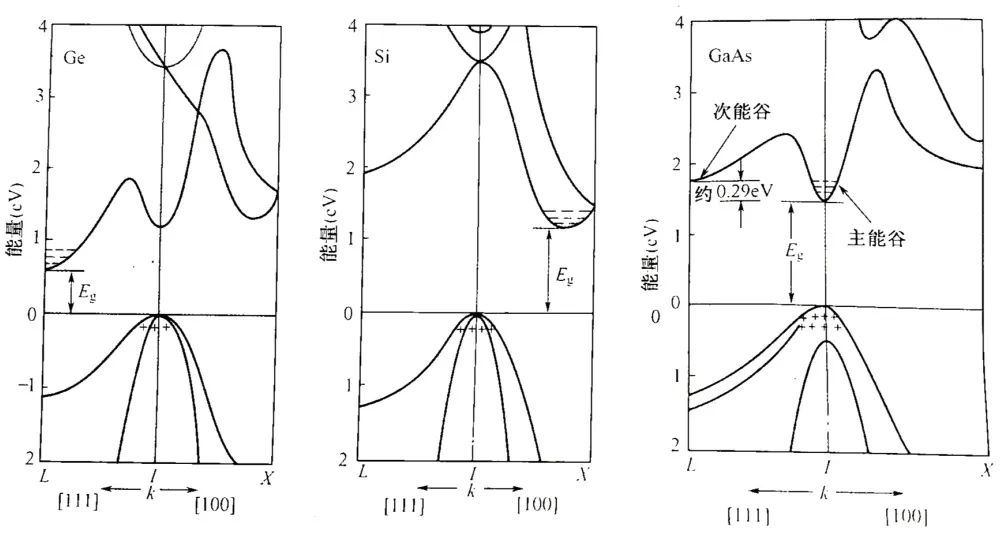
  图中可见，实际材料的导带E(K)曲线和价带E(k)曲线都可能不只一条，每条曲线的极值也可能不只一个。决定材料禁带宽度E(K)的是能量最低的导带极小值(导带底)与能量最高的价带极大值(价带顶)，而不管这两个极值是不是对应于同一个k。   上图呈现了两种跃迁：直接跃迁和间接跃迁。   间接跃迁：导带底和价带顶对应于不同的k，譬如硅和锗，其电子跃迁前、后必有动量变化，我们称其为间接跃迁，相应的禁带叫间接禁带。   直接跃迁：导带底和价带顶对应于同一个k，譬如像砷化镓那样，则电子跃迁前、后没有动量变化，称为直接跃迁，这种能带结构的禁带叫直接禁带。   能带结构的另一关注点是它的对称性。如果一个能带极值不在k空间的中心，则必有若干等价极值存在于各对称点。譬如硅的导带底出现在(100)方向，有6个等价导带底：锗的导带底出现在(111)方向，因此有8个等价的导带底。   导带底是导带电子的最低能量，因此又叫能谷。有些材料的导带还具有比导带底略高一点的极小值并兼备其他一些特征，因而具有特殊的实用价值，譬如砷化镓。为了区别，在这种情况下把导带底称为主能谷，较高的极小值称为次能谷。