利用自适应网格细化功能自动生成最佳网格

 

仿真预处理的目标是根据分析创建所需的网格。在生成同时解析几何和物理特征的网格时，我们的目标是提高计算效率。基于仿真预期，我们可以针对流动特征不明显的特定网格区域进行网格增强。在下图中，我们在车辆周围添加了细化区域，因为我们预计这部分会有大量的物理特征，尤其是在尾流区域。这一过程需要运用大量的专业领域知识，并且非常依赖用户输入的数据。不过，对流动物理特性极少的区域进行过度细化会增加计算成本和仿真时间，这是不可取的。本文将详细介绍 Cadence Fidelity Pointwise 中的自动自适应网格细化功能，该功能可管理数值误差并遵循用户定义的边界，同时解析各种应用中的所有流动特征。

 

1.网格自适应有哪些要求？

 

网格应满足以下条件：

 

符合底层 CAD 几何图形

细化符合局部各向异性边界层

细化较大的和细微的流动特征

 

在自适应网格细化过程中，我们希望保留边界层和近壁面的物理特性，使单元大小平滑渐变，确保求解器正常收敛。在自适应网格细化过程中，有必要定义一个自适应传感器，以便描述需要额外细化的区域。在飞机外部研究中，马赫数是一个合适的自适应变量，而在涡轮机械应用中，可以将速度大小用作自适应传感器。

 

2.使用 Fidelity Pointwise 进行自适应网格细化

 

在 Fidelity Pointwise 中创建基础网格，以启动自适应网格细化。然后，在该网格上运行解。在每个边缘对传感器进行评估，如果传感器在特定位置超过了预定阈值，就会标记为自适应细化。根据点的位置和该区域新的目标单元大小创建点云。然后将点云整合到 Fidelity Pointwise 中的基础网格中，创建更新后的网格。反复进行这一过程，直到解达到与网格无关的状态。

 

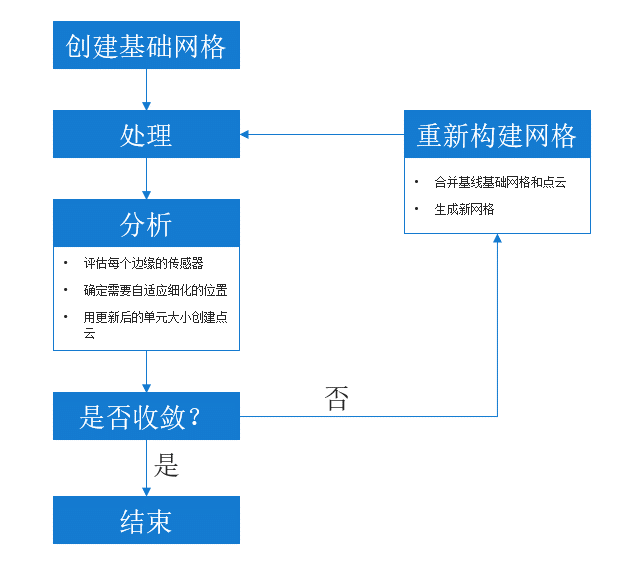
Fidelity Pointwise 中的网格自适应周期

 

3.应用测试用例

 

冲击射流

 

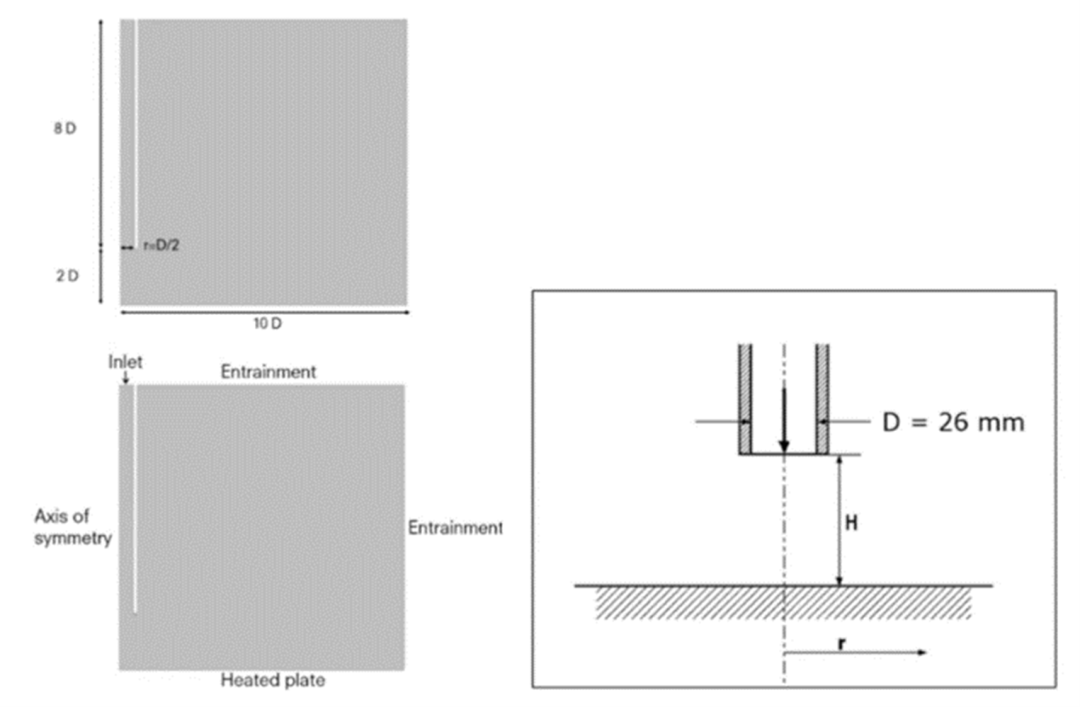
冲击射流的边界条件

 

在上图中，冷射流降落到热板上，边界条件如图所示。

 

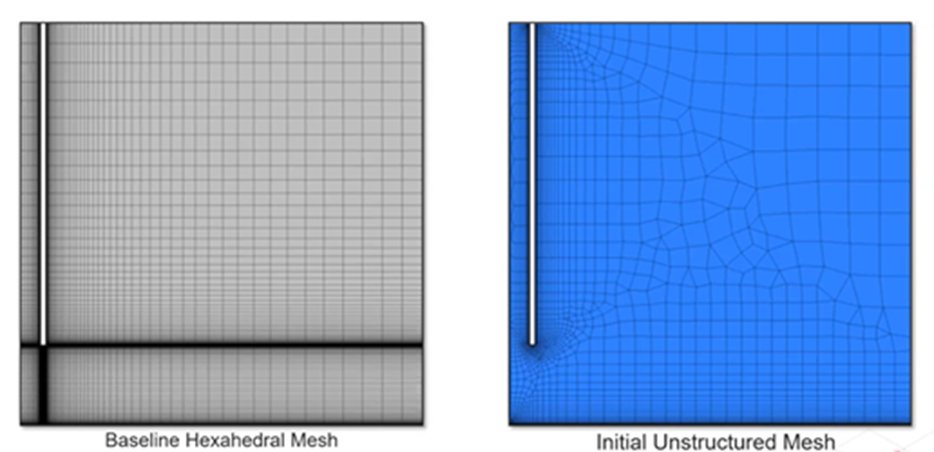
基准网格（左），初始网格（右）

 

本例的目的是比较完整结构化网格和调整后的网格。在上图中，左边的图片显示的是基线基础六面体网格，右边的图片显示的是将根据速度大小进行调整的初始非结构化网格。

 

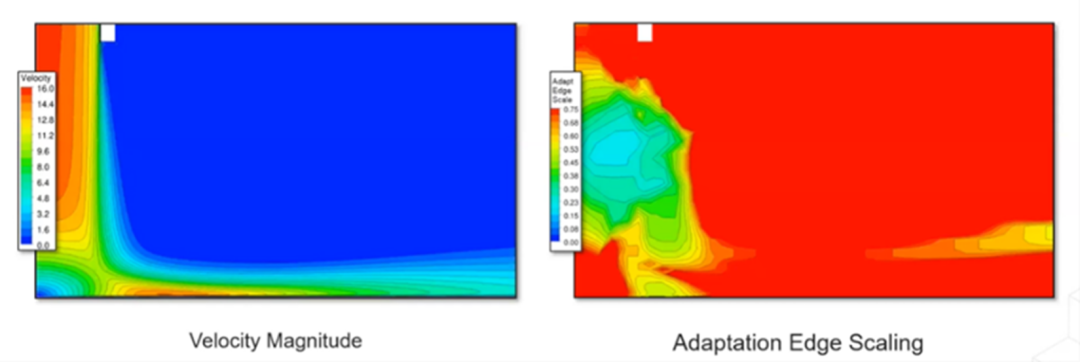
速度大小等值线（左）和自适应边缘缩放（右）

 

右图显示了当前边缘通道所需的缩放比例。自适应过程的重点是射流和板之间的区域。根据解创建点云，有 25% 的节点超过了阈值，因此将进行相应的自适应细化。

 

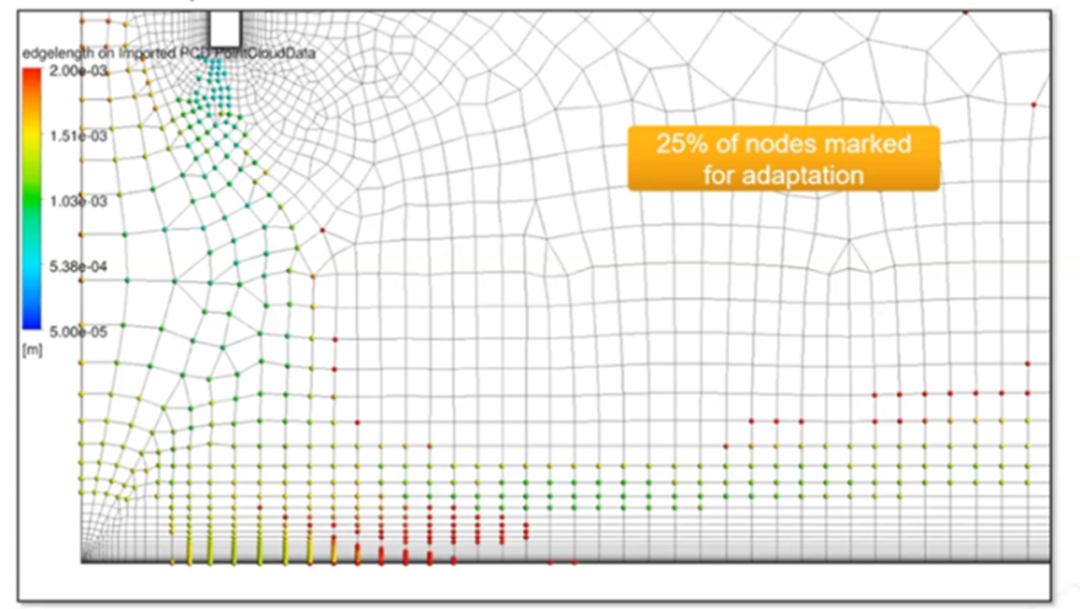
初始点云，有 25% 的节点被标记为自适应节点

 

在第五个周期中，约有 70% 的节点被标记为自适应节点，而在最后一个周期中，94% 的节点被标记为自适应节点。一旦约 90% 的节点被标记为自适应节点，就可以认为已经收敛。此时可以结束迭代。

 

第 5 个周期（左）和第 9 个周期（右）中经过自适应细化的网格

 

检查网格统计数据后发现，与高度细化的六边形网格相比，修改后的网格节点和元素更少。放大冲击区域后，明显发现初始网格并没有准确捕捉到数据。然而，网格在经过每个周期后都有所改进，最终更接近实验数据。

 

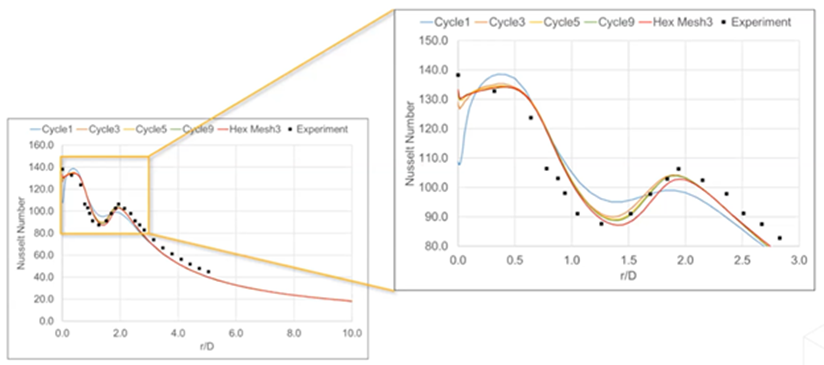
努塞尔数 (Nu) 在经过每个自适应周期后都更接近实验 Nu 值

 

轴流式涡轮机叶

 

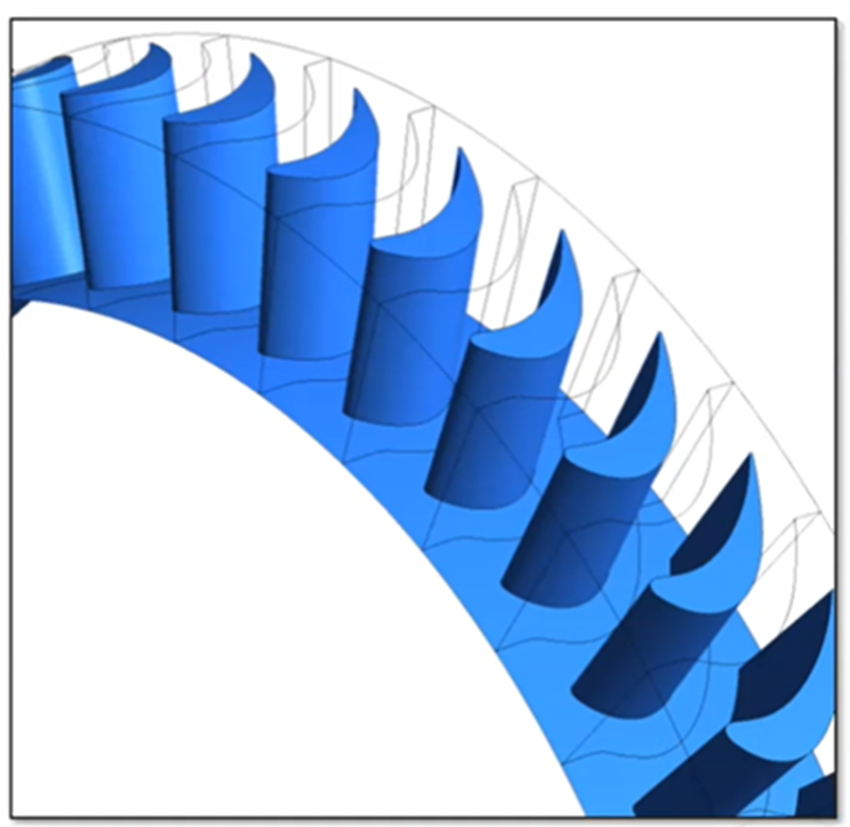
亚琛涡轮机

 

本测试案例中是一台亚琛涡轮机，有 41 个叶片，转速为 3500 RPM。入口和出口流动条件如下表所示：

 

Ptotal（入口）	169,000 Pa
Ttotal （入口）	308 K
A（入口）	49.3°
Poutlet	135,000 Pa（平均）

 

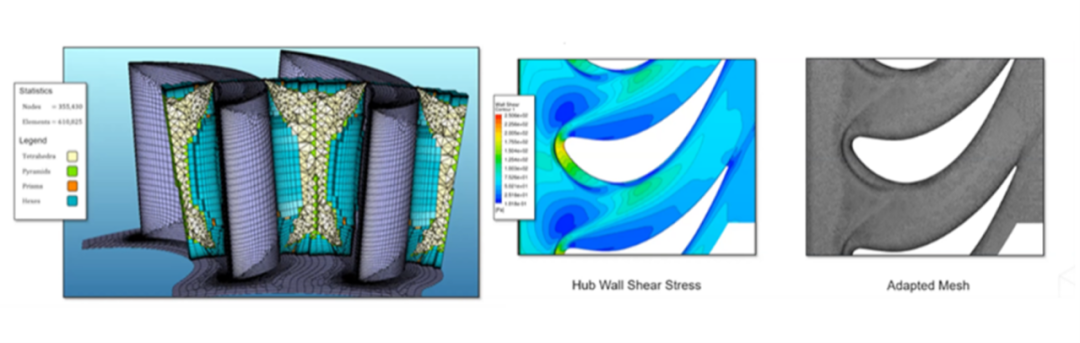
自适应细化的初始网格（左），自适应细化的最终网格 - 叶片区域的切面（右）

 

这里再次使用速度大小作为自适应变量。在经过自适应细化的网格中，冲击波清晰可见。此外，经过自适应细化的最终网格准确地反映了二次涡和冲击波的存在。

 

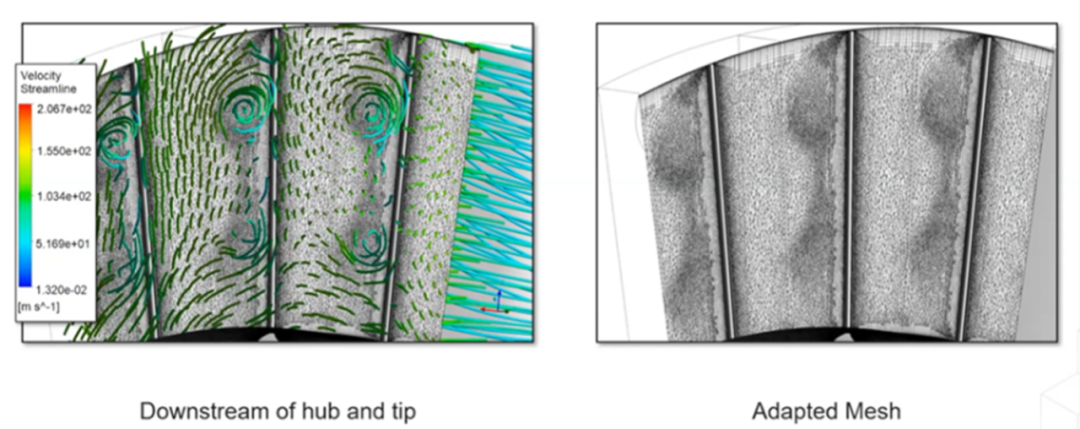
经过自适应细化的网格捕捉到了二次涡流

 

DrivAer 模型

 

 

自适应网格细化也可用于汽车应用，本例中我们使用 DrivAer 模型作为测试案例。将速度大小作为自适应变量。DrivAer 模型的 RANS 仿真使用了 SST 两方程湍流模型。经过自适应的网格和尾流区域的流线如下所示，显示出良好的匹配度和对涡流的准确捕捉。

 

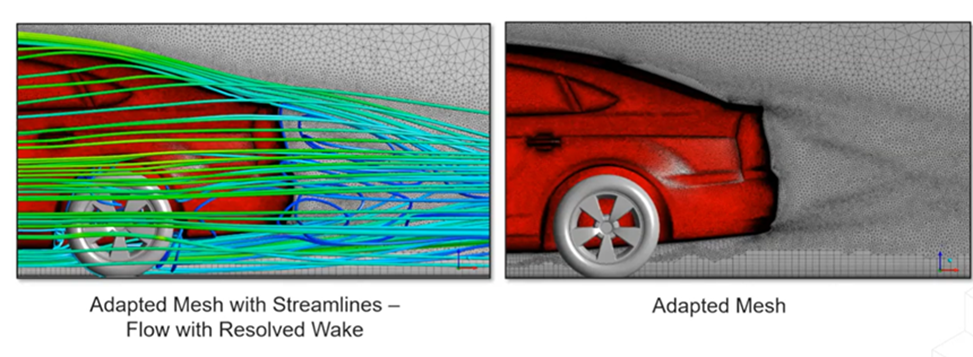
DrivAer 模型经过自适应的网格

 

外部空气动力学

 

DLR F6 模型

 

该测试案例是第二届 AIAA 阻力预测研讨会上的 DLR F6 模型。马赫数为 0.75，迎角为 1°。这里的自适应变量是马赫数。通过自适应网格细化，机翼顶部的冲击波清晰可见。初始表面压力和经过自适应细化后的表面压力如下图所示。经过每个自适应周期后，冲击波都会变得更加清晰。

 

初始网格（左）和经过自适应细化的网格（右）的表面压力

 

观察升力和阻力系数可以发现，每经过一个周期，细化程度都会变得更加精确。这种网格自适应方法可以轻松集成到任何工作流程中。

 

虽然一开始需要花费一些精力进行设置，但一旦设置妥当，剩下的流程就可以自动完成。在自适应周期中，因为每次都会返回到基线基础网格，所以拓扑结构将保持一致。

 

适应周期期间的升力和阻力系数

 

4.高阶网格弯曲

 

高阶网格弯曲是一项新兴技术，对于在计算流体力学（CFD）求解器领域中使用有限元方法（FEM）的设计人员来说，这项技术将成为他们的得力助手。与有限体积法和有限差分法等传统 CFD 方法相比，有限元技术能以较少的元素提高准确度。这要归功于有限元方法在线性元素的边、面和内部引入了额外的顶点（新的自由度）。对于与弯曲几何体相邻的元素，这些新自由度必须位于几何体上，从而改变原始线性元素的形状。当网格中有一组元素向粘性边界聚类时，这一过程会更加困难。内部元素的边和面也必须根据边界元素的曲率进行弯曲，以避免元素反转。

 

对 Cadence Fidelity Pointwise 所使用的 WCN 平滑处理进行研究，允许混合阶网格求解几何曲率。在高度弯曲的几何体附近，元素最高可升阶至四次多项式（四次方），而在远离弯曲几何体的地方，元素仍然保持线性。网格平滑方法使用代价函数来强制保持所需的元素形状和每个元素的正雅可比。当元素在几何体附近弯曲时，粘性网格间距保持不变。研究显示了复杂 3D 配置的效果。