

 反相放大电路运放V+引脚串联电阻过大也会产生输出失调电压?1400字理清原理与计算
反相放大电路运放V+引脚串联电阻过大也会产生输出失调电压?1400字理清原理与计算
描述
Part 01
前言
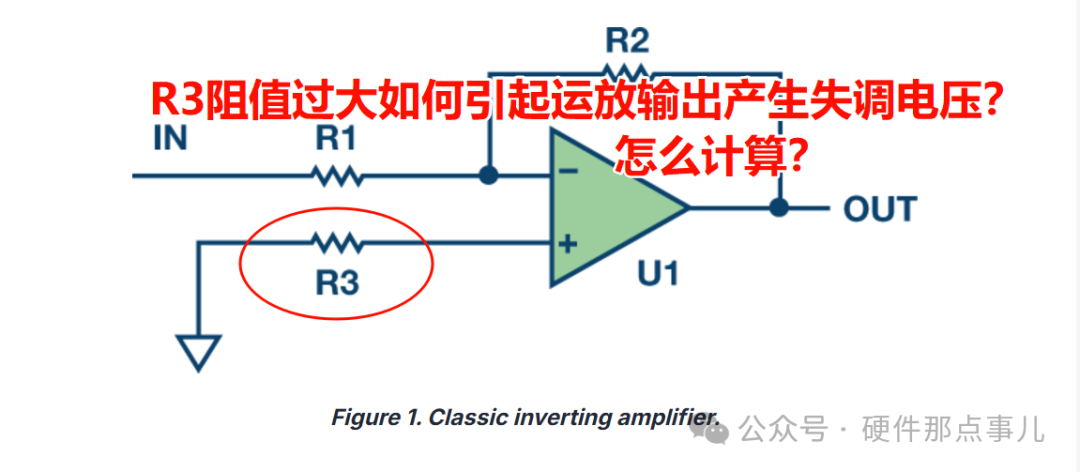
当我们用运放设计电流或者电压采样电路时,如果我们要求的采样精度比较高的话,那么一个绕不开的话题就是噪声,噪声是很多硬件工程师容易忽视又不知如何下手的因素,但是噪声影响是信号处理中的一个重要问题,它会影响采样电路的精度和稳定性,运放电路中的噪声分为两大类,一类是运放内部噪声的影响,另外一类是运放外部噪声的影响,而电阻的热噪声是运放外部噪声影响因素中的一种。 在之前的文章中我们介绍过为了解决运放偏置电流引起的输入失调电压,会在反相放大电路的同相输入端串联一个电阻,如果R3匹配电阻的阻值比较大的话,会引入额外的噪声,进而在运放输出端产生失调电压,如何计算这个噪声呢?
Part 02
如何理解噪声?
噪声是什么?噪声在电路中本质上还是一种信号,只不过它不是你想要的信号,它可能是电流信号,也可能是电压信号。电路中的噪声是一种随机信号,为什么随机呢?如果你对“电子”还有印象,这玩意就是随机乱跑乱撞,虽然是随机的,但是呢它又符合一定的概率分布特性和统计参数,比如著名的分布噪声分布曲线:正态分布,也叫高斯分布。
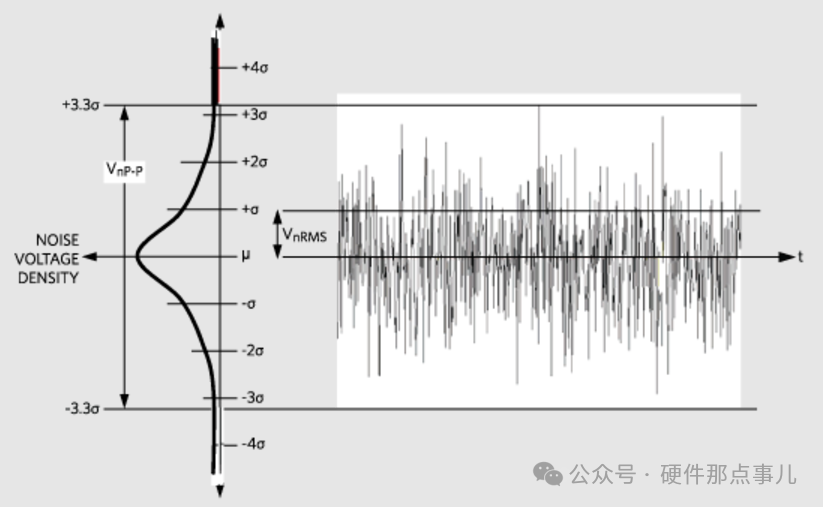
根据中心极限定理,当大量独立随机变量叠加时,其总和趋于服从正态分布,无论原始变量的分布是什么。因此,高斯分布是描述噪声的自然选择,尤其是由大量微观事件叠加而成的噪声,所以你看上面两张图,原本杂乱无章的噪声分布经过概率密度函数一分析,就变得很有章法,数学是不是很神奇,所以要想搞好电路,数学是基本功。 高斯分布的概率密度函数如下:
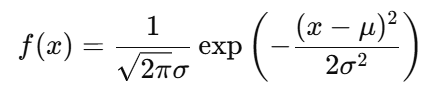
μ: 噪声的平均值(μ反映噪声信号的直流偏移量。理想情况下,噪声的平均值为零,表示正负噪声幅度对称)
σ: 噪声的标准差,表示噪声的幅度的典型分布范围。标准差是一组数据平均值分散程度的一种度量。一个较大的标准差,代表大部分数值和其平均值之间差异较大。

如何理解高斯分布曲线?
在高斯分布中:
68.3%的噪声幅度在±σ内。
95.4%的噪声幅度在±2σ内。
99.7%的噪声幅度在±3σ内。
既然99.7%的噪声幅度都在±3σ内,那么我们就能基于标准差σ计算得到噪声的峰峰值,因为只有知道了噪声的峰峰值才能方便我们计算对测量信号的影响。噪声的有效值约等于标准差σ(当噪声平均值为0时),这样噪声信号的峰峰值计算如下:
σ=Vrms
Vpp≈6*σ
这样我们就能根据噪声的正态分布曲线计算得到噪声的峰峰值。
Part 03
如何计算电阻的热噪声
电阻热噪声是由电阻内部自由电子的热运动产生的无规则波动,噪声幅值呈正态分布,其平均值为零。电阻热噪声电压的计算为在电阻R上,带宽B内的热噪声均方根(RMS)电压为:
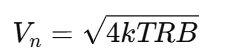
k=1.38×10^-23J/K,是玻尔兹曼常数
T:电阻的绝对温度(开尔文,K),T=273+摄氏温度
R:电阻值(Ω)
B:噪声的带宽(Hz)
可以看出当阻值一定,温度一定时,带宽对噪声的影响至关重要,带宽越宽,噪声越大。 比如环境温度为25℃,电阻阻值为100K,带宽为1Hz,可以计算得到电阻的热噪声为40nV。
Part 04
如何计算电阻的热噪声对运放输出的影响
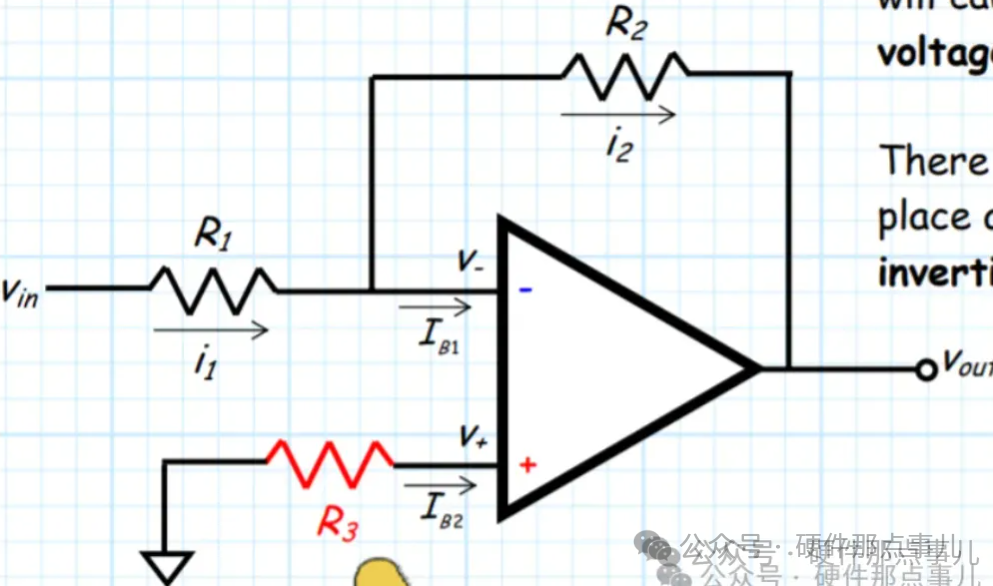
如果下面的反相放大电路的放大倍数是100,电阻R3的阻值是100K,环境温度是25℃,噪声带宽是100KHz的话,对应的输出噪声电压有效值为: Vos=40nV*√100KHz*100≈1.27mV 1.27mV的输出失调电压对于一些高精度信号测量来说已经是不小的影响了,所以如果你有高精度测量应用,不可忽视电阻热噪声的影响!
-
1200字搞懂运放电路中输入失调电压的分析,计算,以及选型对策2024-10-11 5201
-
运放失调电压补偿方法有哪些2024-08-15 3851
-
失调电压Vos定义 各类运放失调电压范围 失调电压产生原因2023-11-06 4486
-
运放失调电压如何消除2023-09-22 6943
-
运放为什么有失调电压?2023-09-21 2656
-
运放的失调电压的调整引脚2021-11-19 3882
-
如何使用失调电阻消除运放输出失调电压消除2021-02-28 1762
-
深入浅出!运放平衡电阻的理解2020-07-12 4222
-
失调电压调整引脚去哪了?2018-09-21 2788
-
运放失调电压自动补偿设计与实现2017-11-29 18157
-
运放的失调电压是什么?2009-04-22 9197
全部0条评论

快来发表一下你的评论吧 !

