

иҒҡзұ»еҲҶжһҗз»Ҹе…ёз®—жі•и®Іи§ЈеҸҠе®һзҺ°
з”өеӯҗиҜҙ
жҸҸиҝ°
еёёз”ЁиҒҡзұ»з®—жі•жҜ”иҫғеҲҶжһҗ
K-pototypesз®—жі•
K-pototypesз®—жі•з»“еҗҲдәҶK-meansж–№жі•е’Ңж №жҚ®K-meansж–№жі•ж”№иҝӣзҡ„иғҪеӨҹеӨ„зҗҶз¬ҰеҸ·еұһжҖ§зҡ„K-modesж–№жі•пјҢеҗҢK-meansж–№жі•зӣёжҜ”пјҢK-pototypes з®—жі•иғҪеӨҹеӨ„зҗҶз¬ҰеҸ·еұһжҖ§гҖӮ
CLARANSз®—жі•пјҲеҲ’еҲҶж–№жі•пјү
CLARANSз®—жі•еҚійҡҸжңәжҗңзҙўиҒҡзұ»з®—жі•пјҢжҳҜдёҖз§ҚеҲҶеүІиҒҡзұ»ж–№жі•гҖӮе®ғйҰ–е…ҲйҡҸжңәйҖүжӢ©дёҖдёӘзӮ№дҪңдёәеҪ“еүҚзӮ№пјҢ然еҗҺйҡҸжңәжЈҖжҹҘе®ғе‘ЁеӣҙдёҚи¶…иҝҮеҸӮж•°Maxneighbor дёӘзҡ„дёҖдәӣйӮ»жҺҘзӮ№пјҢеҒҮеҰӮжүҫеҲ°дёҖдёӘжҜ”е®ғжӣҙеҘҪзҡ„йӮ»жҺҘзӮ№пјҢеҲҷжҠҠе®ғ移дәәиҜҘйӮ»жҺҘзӮ№пјҢеҗҰеҲҷжҠҠиҜҘзӮ№дҪңдёәеұҖйғЁжңҖе°ҸйҮҸгҖӮ然еҗҺеҶҚйҡҸжңәйҖүжӢ©дёҖдёӘзӮ№жқҘеҜ»жүҫеҸҰдёҖдёӘеұҖйғЁжңҖе°ҸйҮҸпјҢзӣҙиҮіжүҖжүҫ еҲ°зҡ„еұҖйғЁжңҖе°ҸйҮҸж•°зӣ®иҫҫеҲ°з”ЁжҲ·иҰҒжұӮдёәжӯўгҖӮиҜҘз®—жі•иҰҒжұӮиҒҡзұ»зҡ„еҜ№иұЎеҝ…йЎ»йғҪйў„е…Ҳи°ғдәәеҶ…еӯҳпјҢ并且йңҖеӨҡж¬Ўжү«жҸҸж•°жҚ®йӣҶпјҢиҝҷеҜ№еӨ§ж•°жҚ®йҮҸиҖҢиЁҖпјҢж— и®әж—¶й—ҙеӨҚжқӮеәҰиҝҳжҳҜз©әй—ҙеӨҚжқӮеәҰ йғҪзӣёеҪ“еӨ§гҖӮиҷҪйҖҡиҝҮеј•дәәR-ж ‘з»“жһ„еҜ№е…¶жҖ§иғҪиҝӣиЎҢж”№е–„пјҢдҪҝд№ӢиғҪеӨҹеӨ„зҗҶеҹәдәҺзЈҒзӣҳзҡ„еӨ§еһӢж•°жҚ®еә“пјҢдҪҶR*-ж ‘зҡ„жһ„йҖ е’Ңз»ҙжҠӨд»Јд»·еӨӘеӨ§гҖӮиҜҘз®—жі•еҜ№и„Ҹж•°жҚ®е’ҢејӮеёёж•°жҚ®дёҚж•Ҹ ж„ҹпјҢдҪҶеҜ№ж•°жҚ®зү©дәәйЎәеәҸејӮеёёж•Ҹж„ҹпјҢдё”еҸӘиғҪеӨ„зҗҶеҮёеҪўжҲ–зҗғеҪўиҫ№з•ҢиҒҡзұ»гҖӮ
BIRCHз®—жі•пјҲеұӮж¬Ўж–№жі•пјү
BIRCHз®—жі•еҚіе№іиЎЎиҝӯд»ЈеүҠеҮҸиҒҡзұ»жі•пјҢе…¶ж ёеҝғжҳҜз”ЁдёҖдёӘиҒҡзұ»зү№еҫҒ3е…ғз»„иЎЁзӨәдёҖдёӘз°Үзҡ„жңүе…ідҝЎжҒҜпјҢд»ҺиҖҢдҪҝдёҖз°ҮзӮ№зҡ„иЎЁзӨәеҸҜз”ЁеҜ№еә”зҡ„иҒҡзұ»зү№еҫҒпјҢиҖҢдёҚеҝ…з”Ёе…·дҪ“зҡ„дёҖ з»„зӮ№жқҘиЎЁзӨәгҖӮе®ғйҖҡиҝҮжһ„йҖ ж»Ўи¶іеҲҶж”Ҝеӣ еӯҗе’Ңз°Үзӣҙеҫ„йҷҗеҲ¶зҡ„иҒҡзұ»зү№еҫҒж ‘жқҘжұӮиҒҡзұ»гҖӮBIRCHз®—жі•йҖҡиҝҮиҒҡзұ»зү№еҫҒеҸҜд»Ҙж–№дҫҝең°иҝӣиЎҢдёӯеҝғгҖҒеҚҠеҫ„гҖҒзӣҙеҫ„еҸҠзұ»еҶ…гҖҒзұ»й—ҙи·қзҰ»зҡ„иҝҗ з®—гҖӮз®—жі•зҡ„иҒҡзұ»зү№еҫҒж ‘жҳҜдёҖдёӘе…·жңүдёӨдёӘеҸӮж•°еҲҶжһқеӣ еӯҗBе’Ңзұ»зӣҙеҫ„Tзҡ„й«ҳеәҰе№іиЎЎж ‘гҖӮеҲҶжһқеӣ еӯҗ规е®ҡдәҶж ‘зҡ„жҜҸдёӘиҠӮзӮ№еӯҗеҘізҡ„жңҖеӨҡдёӘж•°пјҢиҖҢзұ»зӣҙеҫ„дҪ“зҺ°дәҶеҜ№дёҖзұ»зӮ№зҡ„зӣҙеҫ„еӨ§ е°Ҹзҡ„йҷҗеҲ¶еҚіиҝҷдәӣзӮ№еңЁеӨҡеӨ§иҢғеӣҙеҶ…еҸҜд»ҘиҒҡдёәдёҖзұ»пјҢйқһеҸ¶еӯҗз»“зӮ№дёәе®ғзҡ„еӯҗеҘізҡ„жңҖеӨ§е…ій”®еӯ—пјҢеҸҜд»Ҙж №жҚ®иҝҷдәӣе…ій”®еӯ—иҝӣиЎҢжҸ’дәәзҙўеј•пјҢе®ғжҖ»з»“дәҶе…¶еӯҗеҘізҡ„дҝЎжҒҜгҖӮ
иҒҡзұ»зү№еҫҒж ‘еҸҜд»ҘеҠЁжҖҒжһ„йҖ пјҢеӣ жӯӨдёҚиҰҒжұӮжүҖжңүж•°жҚ®иҜ»дәәеҶ…еӯҳпјҢиҖҢеҸҜд»ҘеңЁеӨ–еӯҳдёҠйҖҗдёӘиҜ»дәәгҖӮж–°зҡ„ж•°жҚ®йЎ№жҖ»жҳҜжҸ’дәәеҲ°ж ‘дёӯдёҺиҜҘж•°жҚ®и·қзҰ»жңҖиҝ‘зҡ„еҸ¶еӯҗдёӯгҖӮеҰӮжһңжҸ’дәәеҗҺдҪҝеҫ— иҜҘеҸ¶еӯҗзҡ„зӣҙеҫ„еӨ§дәҺзұ»зӣҙеҫ„TпјҢеҲҷжҠҠиҜҘеҸ¶еӯҗиҠӮзӮ№еҲҶиЈӮгҖӮе…¶е®ғеҸ¶еӯҗз»“зӮ№д№ҹйңҖиҰҒжЈҖжҹҘжҳҜеҗҰи¶…иҝҮеҲҶжһқеӣ еӯҗжқҘеҲӨж–ӯе…¶еҲҶиЈӮдёҺеҗҰпјҢзӣҙиҮіиҜҘж•°жҚ®жҸ’е…ҘеҲ°еҸ¶еӯҗдёӯпјҢ并且满足дёҚи¶…иҝҮзұ»зӣҙ еҫ„пјҢиҖҢжҜҸдёӘйқһеҸ¶еӯҗиҠӮзӮ№зҡ„еӯҗеҘідёӘж•°дёҚеӨ§дәҺеҲҶжһқеӣ еӯҗгҖӮз®—жі•иҝҳеҸҜд»ҘйҖҡиҝҮж”№еҸҳзұ»зӣҙеҫ„дҝ®ж”№зү№еҫҒж ‘еӨ§е°ҸпјҢжҺ§еҲ¶е…¶еҚ еҶ…еӯҳе®№йҮҸгҖӮ
BIRCHз®—жі•йҖҡиҝҮдёҖж¬Ўжү«жҸҸе°ұеҸҜд»ҘиҝӣиЎҢиҫғеҘҪзҡ„иҒҡзұ»пјҢз”ұжӯӨеҸҜи§ҒпјҢиҜҘз®—жі•йҖӮеҗҲдәҺеӨ§ж•°жҚ®йҮҸгҖӮеҜ№дәҺз»ҷе®ҡзҡ„Mе…ҶеҶ…еӯҳз©әй—ҙпјҢе…¶з©әй—ҙеӨҚжқӮеәҰдёәOпјҲMпјүпјҢж—¶й—ҙй—ҙеӨҚжқӮеәҰ дёәOпјҲdNBlnBпјҲM/PпјүпјүгҖӮе…¶дёӯdдёәз»ҙж•°пјҢNдёәиҠӮзӮ№ж•°пјҢPдёәеҶ…еӯҳйЎөзҡ„еӨ§е°ҸпјҢBдёәз”ұPеҶіе®ҡзҡ„еҲҶжһқеӣ еӯҗгҖӮI/OиҠұиҙ№дёҺж•°жҚ®йҮҸжҲҗзәҝжҖ§е…ізі»гҖӮBIRCHз®—жі• еҸӘйҖӮз”ЁдәҺзұ»зҡ„еҲҶеёғе‘ҲеҮёеҪўеҸҠзҗғеҪўзҡ„жғ…еҶөпјҢ并且з”ұдәҺBIRCHз®—жі•йңҖжҸҗдҫӣжӯЈзЎ®зҡ„иҒҡзұ»дёӘж•°е’Ңз°Үзӣҙеҫ„йҷҗеҲ¶пјҢеҜ№дёҚеҸҜи§Ҷзҡ„й«ҳз»ҙж•°жҚ®дёҚеҸҜиЎҢгҖӮ
CUREз®—жі•пјҲеұӮж¬Ўж–№жі•пјү
CUREз®—жі•еҚідҪҝз”Ёд»ЈиЎЁзӮ№зҡ„иҒҡзұ»ж–№жі•гҖӮиҜҘз®—жі•е…ҲжҠҠжҜҸдёӘж•°жҚ®зӮ№зңӢжҲҗдёҖзұ»пјҢ然еҗҺеҗҲ并и·қзҰ»жңҖиҝ‘зҡ„зұ»зӣҙиҮізұ»дёӘж•°дёәжүҖиҰҒжұӮзҡ„дёӘж•°дёәжӯўгҖӮCUREз®—жі•е°Ҷдј з»ҹеҜ№зұ»зҡ„ иЎЁзӨәж–№жі•иҝӣиЎҢдәҶж”№иҝӣпјҢеӣһйҒҝдәҶз”ЁжүҖжңүзӮ№жҲ–з”Ёдёӯеҝғе’ҢеҚҠеҫ„жқҘиЎЁзӨәдёҖдёӘзұ»пјҢиҖҢжҳҜд»ҺжҜҸдёҖдёӘзұ»дёӯжҠҪеҸ–еӣәе®ҡж•°йҮҸгҖҒеҲҶеёғиҫғеҘҪзҡ„зӮ№дҪңдёәжҸҸиҝ°жӯӨзұ»зҡ„д»ЈиЎЁзӮ№пјҢ并е°ҶиҝҷдәӣзӮ№д№ҳд»ҘдёҖдёӘ йҖӮеҪ“зҡ„收缩еӣ еӯҗпјҢдҪҝе®ғ们жӣҙйқ иҝ‘зұ»зҡ„дёӯеҝғзӮ№гҖӮе°ҶдёҖдёӘзұ»з”Ёд»ЈиЎЁзӮ№иЎЁзӨәпјҢдҪҝеҫ—зұ»зҡ„еӨ–延еҸҜд»Ҙеҗ‘йқһзҗғеҪўзҡ„еҪўзҠ¶жү©еұ•пјҢд»ҺиҖҢеҸҜи°ғж•ҙзұ»зҡ„еҪўзҠ¶д»ҘиЎЁиҫҫйӮЈдәӣйқһзҗғеҪўзҡ„зұ»гҖӮеҸҰеӨ–пјҢ 收缩еӣ еӯҗзҡ„дҪҝз”ЁеҮҸе°ҸдәҶе—“йҹіеҜ№иҒҡзұ»зҡ„еҪұе“ҚгҖӮCUREз®—жі•йҮҮз”ЁйҡҸжңәжҠҪж ·дёҺеҲҶеүІзӣёз»“еҗҲзҡ„еҠһжі•жқҘжҸҗй«ҳз®—жі•зҡ„з©әй—ҙе’Ңж—¶й—ҙж•ҲзҺҮпјҢ并且еңЁз®—жі•дёӯз”ЁдәҶе Ҷе’ҢK-dж ‘з»“жһ„жқҘжҸҗ й«ҳз®—жі•ж•ҲзҺҮгҖӮ
DBSCANз®—жі•пјҲеҹәдәҺеҜҶеәҰзҡ„ж–№жі•пјү
DBSCANз®—жі•еҚіеҹәдәҺеҜҶеәҰзҡ„иҒҡзұ»з®—жі•гҖӮиҜҘз®—жі•еҲ©з”Ёзұ»зҡ„еҜҶеәҰиҝһйҖҡжҖ§еҸҜд»Ҙеҝ«йҖҹеҸ‘зҺ°д»»ж„ҸеҪўзҠ¶зҡ„зұ»гҖӮе…¶еҹәжң¬жҖқжғіжҳҜпјҡеҜ№дәҺдёҖдёӘзұ»дёӯзҡ„жҜҸдёӘеҜ№иұЎпјҢеңЁе…¶з»ҷе®ҡеҚҠеҫ„зҡ„ йўҶеҹҹдёӯеҢ…еҗ«зҡ„еҜ№иұЎдёҚиғҪе°‘дәҺжҹҗдёҖз»ҷе®ҡзҡ„жңҖе°Ҹж•°зӣ®гҖӮеңЁDBSCANз®—жі•дёӯпјҢеҸ‘зҺ°дёҖдёӘзұ»зҡ„иҝҮзЁӢжҳҜеҹәдәҺиҝҷж ·зҡ„дәӢе®һпјҡдёҖдёӘзұ»иғҪеӨҹиў«е…¶дёӯзҡ„д»»ж„ҸдёҖдёӘж ёеҝғеҜ№иұЎжүҖзЎ®е®ҡгҖӮдёә дәҶеҸ‘зҺ°дёҖдёӘзұ»пјҢDBSCANе…Ҳд»ҺеҜ№иұЎйӣҶDдёӯжүҫеҲ°д»»ж„ҸдёҖеҜ№иұЎPпјҢ并жҹҘжүҫDдёӯе…ідәҺе…іеҫ„Epsе’ҢжңҖе°ҸеҜ№иұЎж•°Minptsзҡ„д»ҺPеҜҶеәҰеҸҜиҫҫзҡ„жүҖжңүеҜ№иұЎгҖӮеҰӮжһңPжҳҜж ёеҝғ еҜ№иұЎпјҢеҚіеҚҠеҫ„дёәEpsзҡ„Pзҡ„йӮ»еҹҹдёӯеҢ…еҗ«зҡ„еҜ№иұЎдёҚе°‘дәҺMinptsпјҢеҲҷж №жҚ®з®—жі•пјҢеҸҜд»ҘжүҫеҲ°дёҖдёӘе…ідәҺеҸӮж•°Epsе’ҢMinptsзҡ„зұ»гҖӮеҰӮжһңPжҳҜдёҖдёӘиҫ№з•ҢзӮ№пјҢеҲҷеҚҠ еҫ„дёәEpsзҡ„PйӮ»еҹҹеҢ…еҗ«зҡ„еҜ№иұЎе°‘дәҺMinptsпјҢPиў«жҡӮж—¶ж ҮжіЁдёәеҷӘеЈ°зӮ№гҖӮ然еҗҺпјҢDBSCANеӨ„зҗҶDдёӯзҡ„дёӢдёҖдёӘеҜ№иұЎгҖӮ
еҜҶеәҰеҸҜиҫҫеҜ№иұЎзҡ„иҺ·еҸ–жҳҜйҖҡиҝҮдёҚж–ӯжү§иЎҢеҢәеҹҹжҹҘиҜўжқҘе®һзҺ°зҡ„гҖӮдёҖдёӘеҢәеҹҹжҹҘиҜўиҝ”еӣһжҢҮе®ҡеҢәеҹҹдёӯзҡ„жүҖжңүеҜ№иұЎгҖӮдёәдәҶжңүж•Ҳең°жү§иЎҢеҢәеҹҹжҹҘиҜўпјҢDBSCANз®—жі•дҪҝз”ЁдәҶз©әй—ҙжҹҘ иҜўR-ж ‘з»“жһ„гҖӮеңЁиҝӣиЎҢиҒҡзұ»еүҚпјҢеҝ…йЎ»е»әз«Ӣй’ҲеҜ№жүҖжңүж•°жҚ®зҡ„R*-ж ‘гҖӮеҸҰеӨ–пјҢDBSCANиҰҒжұӮз”ЁжҲ·жҢҮе®ҡдёҖдёӘе…ЁеұҖеҸӮж•°EpsпјҲдёәдәҶеҮҸе°‘и®Ўз®—йҮҸпјҢйў„е…ҲзЎ®е®ҡеҸӮж•° MinptsпјүгҖӮдёәдәҶзЎ®е®ҡеҸ–еҖјпјҢDBSCANи®Ўз®—д»»ж„ҸеҜ№иұЎдёҺе®ғзҡ„第kдёӘжңҖдёҙиҝ‘зҡ„еҜ№иұЎд№Ӣй—ҙзҡ„и·қзҰ»гҖӮ然еҗҺпјҢж №жҚ®жұӮеҫ—зҡ„и·қзҰ»з”ұе°ҸеҲ°еӨ§жҺ’еәҸпјҢ并з»ҳеҮәжҺ’еәҸеҗҺзҡ„еӣҫпјҢз§° еҒҡk-distеӣҫгҖӮk-distеӣҫдёӯзҡ„жЁӘеқҗж ҮиЎЁзӨәж•°жҚ®еҜ№иұЎдёҺе®ғзҡ„第kдёӘжңҖиҝ‘зҡ„еҜ№иұЎй—ҙзҡ„и·қзҰ»пјӣзәөеқҗж ҮдёәеҜ№еә”дәҺжҹҗдёҖk-distи·қзҰ»еҖјзҡ„ж•°жҚ®еҜ№иұЎзҡ„дёӘж•°гҖӮ R*-ж ‘зҡ„е»әз«Ӣе’Ңk-distеӣҫзҡ„з»ҳеҲ¶йқһеёёж¶ҲиҖ—ж—¶й—ҙгҖӮжӯӨеӨ–пјҢдёәдәҶеҫ—еҲ°иҫғеҘҪзҡ„иҒҡзұ»з»“жһңпјҢз”ЁжҲ·еҝ…йЎ»ж №жҚ®k-distеӣҫпјҢйҖҡиҝҮиҜ•жҺўйҖүе®ҡдёҖдёӘжҜ”иҫғеҗҲйҖӮзҡ„EpsеҖјгҖӮ DBSCANз®—жі•дёҚиҝӣиЎҢд»»дҪ•зҡ„йў„еӨ„зҗҶиҖҢзӣҙжҺҘеҜ№ж•ҙдёӘж•°жҚ®йӣҶиҝӣиЎҢиҒҡзұ»ж“ҚдҪңгҖӮеҪ“ж•°жҚ®йҮҸйқһеёёеӨ§ж—¶пјҢе°ұеҝ…йЎ»жңүеӨ§еҶ…еӯҳйҮҸж”ҜжҢҒпјҢI/Oж¶ҲиҖ—д№ҹйқһеёёеӨ§гҖӮе…¶ж—¶й—ҙеӨҚжқӮеәҰдёә OпјҲnlognпјүпјҲnдёәж•°жҚ®йҮҸпјүпјҢиҒҡзұ»иҝҮзЁӢзҡ„еӨ§йғЁеҲҶж—¶й—ҙз”ЁеңЁеҢәеҹҹжҹҘиҜўж“ҚдҪңдёҠгҖӮDBSCANз®—жі•еҜ№еҸӮж•°EpsеҸҠMinptsйқһеёёж•Ҹж„ҹпјҢдё”иҝҷдёӨдёӘеҸӮж•°еҫҲйҡҫзЎ®е®ҡгҖӮ
CLIQUEз®—жі•пјҲз»јеҗҲдәҶеҹәдәҺеҜҶеәҰе’ҢеҹәдәҺзҪ‘ж јзҡ„з®—жі•пјү
CLIQUEз®—жі•еҚіиҮӘеҠЁеӯҗз©әй—ҙиҒҡзұ»з®—жі•гҖӮиҜҘз®—жі•еҲ©з”ЁиҮӘйЎ¶еҗ‘дёҠж–№жі•жұӮеҮәеҗ„дёӘеӯҗз©әй—ҙзҡ„иҒҡзұ»еҚ•е…ғгҖӮCLUQUEз®—жі•дё»иҰҒз”ЁдәҺжүҫеҮәеңЁй«ҳз»ҙж•°жҚ®з©әй—ҙдёӯеӯҳеңЁзҡ„дҪҺз»ҙ иҒҡзұ»гҖӮдёәдәҶжұӮеҮәdз»ҙз©әй—ҙиҒҡзұ»пјҢеҝ…йЎ»з»„еҗҲз»ҷеҮәжүҖжңүd-1з»ҙеӯҗз©әй—ҙзҡ„иҒҡзұ»пјҢеҜјиҮҙе…¶з®—жі•зҡ„з©әй—ҙе’Ңж—¶й—ҙж•ҲзҺҮйғҪиҫғдҪҺпјҢиҖҢдё”иҰҒжұӮз”ЁжҲ·иҫ“е…ҘдёӨдёӘеҸӮж•°пјҡж•°жҚ®еҸ–еҖјз©әй—ҙзӯүй—ҙйҡ” и·қзҰ»е’ҢеҜҶеәҰйҳ”еҖјгҖӮиҝҷ2дёӘеҸӮж•°дёҺж ·жңЁж•°жҚ®зҙ§еҜҶзӣёе…іпјҢз”ЁжҲ·дёҖиҲ¬йҡҫд»ҘзЎ®е®ҡгҖӮCLIQUEз®—жі•еҜ№ж•°жҚ®иҫ“дәәйЎәеәҸдёҚж•Ҹж„ҹгҖӮ
еҹәдәҺдёҠиҝ°еҲҶжһҗпјҢжҲ‘们еҫ—еҲ°еҗ„иҒҡзұ»з®—жі•зҡ„жҜ”иҫғз»“жһңпјҢз»“и®әеҰӮдёӢпјҡ

K еқҮеҖјз®—жі•иҜҰи§ЈеҸҠе®һзҺ°
з®—жі•жөҒзЁӢ
K еқҮеҖјз®—жі•пјҢеә”иҜҘжҳҜиҒҡзұ»з®—жі•дёӯжңҖдёәеҹәзЎҖдҪҶд№ҹжңҖдёәйҮҚиҰҒзҡ„з®—жі•гҖӮе…¶з®—жі•жөҒзЁӢеҰӮдёӢпјҡ
йҡҸжңәзҡ„еҸ– k дёӘзӮ№дҪңдёә k дёӘеҲқе§ӢиҙЁеҝғпјӣ
и®Ўз®—е…¶д»–зӮ№еҲ°иҝҷдёӘ k дёӘиҙЁеҝғзҡ„и·қзҰ»пјӣ
еҰӮжһңжҹҗдёӘзӮ№ p зҰ»з¬¬ n дёӘиҙЁеҝғзҡ„и·қзҰ»жӣҙиҝ‘пјҢеҲҷиҜҘзӮ№еұһдәҺ cluster nпјҢ并еҜ№е…¶жү“ж ҮзӯҫпјҢж ҮжіЁ point p.label=nпјҢе…¶дёӯ nгҖҠ=kпјӣ
и®Ўз®—еҗҢдёҖ cluster дёӯпјҢд№ҹе°ұжҳҜзӣёеҗҢ label зҡ„зӮ№еҗ‘йҮҸзҡ„е№іеқҮеҖјпјҢдҪңдёәж–°зҡ„иҙЁеҝғпјӣ
иҝӯд»ЈиҮіжүҖжңүиҙЁеҝғйғҪдёҚеҸҳеҢ–дёәжӯўпјҢеҚіз®—жі•з»“жқҹгҖӮ
еҪ“然算法е®һзҺ°зҡ„ж–№жі•жңүеҫҲеӨҡпјҢжҜ”еҰӮеңЁйҖүжӢ©еҲқе§ӢиҙЁеҝғж—¶пјҢеҸҜд»ҘйҡҸжңәйҖүжӢ© k дёӘпјҢд№ҹеҸҜд»ҘйҡҸжңәйҖүжӢ© k дёӘзҰ»еҫ—жңҖиҝңзҡ„зӮ№зӯүзӯүпјҢж–№жі•дёҚе°ҪзӣёеҗҢгҖӮ
K еҖјдј°и®Ў
еҜ№дәҺ k еҖјпјҢеҝ…йЎ»жҸҗеүҚзҹҘйҒ“пјҢиҝҷд№ҹжҳҜ kmeans з®—жі•зҡ„дёҖдёӘзјәзӮ№гҖӮеҪ“然еҜ№дәҺ k еҖјпјҢжҲ‘们еҸҜд»ҘжңүеҫҲеӨҡз§Қж–№жі•иҝӣиЎҢдј°и®ЎгҖӮжң¬ж–ҮдёӯпјҢжҲ‘们йҮҮз”Ёе№іеқҮзӣҙеҫ„жі•жқҘиҝӣиЎҢ k зҡ„дј°и®ЎгҖӮ
д№ҹе°ұжҳҜиҜҙпјҢйҰ–е…Ҳи§ҶжүҖжңүзҡ„зӮ№дёәдёҖдёӘеӨ§зҡ„ж•ҙдҪ“ clusterпјҢи®Ўз®—жүҖжңүзӮ№д№Ӣй—ҙи·қзҰ»зҡ„е№іеқҮеҖјдҪңдёәиҜҘ cluster зҡ„е№іеқҮзӣҙеҫ„гҖӮйҖүжӢ©еҲқе§ӢиҙЁеҝғзҡ„ж—¶еҖҷпјҢе…ҲйҖүжӢ©жңҖиҝңзҡ„дёӨдёӘзӮ№пјҢжҺҘдёӢжқҘд»ҺиҝҷжңҖдёӨдёӘзӮ№ејҖе§ӢпјҢдёҺиҝҷжңҖдёӨдёӘзӮ№и·қзҰ»йғҪеҫҲиҝңзҡ„зӮ№пјҲиҝңзҡ„зЁӢеәҰдёәпјҢиҜҘзӮ№еҲ°д№ӢеүҚйҖүжӢ©зҡ„жңҖиҝңзҡ„дёӨдёӘзӮ№зҡ„и·қзҰ»йғҪеӨ§дәҺж•ҙдҪ“ cluster зҡ„е№іеқҮзӣҙеҫ„пјүеҸҜи§Ҷдёәж–°еҸ‘зҺ°зҡ„иҙЁеҝғпјҢеҗҰеҲҷдёҚи§Ҷд№ӢдёәиҙЁеҝғгҖӮи®ҫжғідёҖдёӢпјҢеҰӮжһңеҲ©з”Ёе№іеқҮеҚҠеҫ„жҲ–е№іеқҮзӣҙеҫ„иҝҷдёҖдёӘжҢҮж ҮпјҢиӢҘжҲ‘们зҢңжғізҡ„ K еҖјеӨ§дәҺжҲ–зӯүдәҺзңҹе®һзҡ„ K еҖјпјҢд№ҹе°ұжҳҜз°Үзҡ„зңҹе®һж•°зӣ®пјҢйӮЈд№ҲиҜҘжҢҮж Үзҡ„дёҠеҚҮи¶ӢеҠҝдјҡеҫҲзј“ж…ўпјҢдҪҶжҳҜеҰӮжһңжҲ‘们з»ҷеҮәзҡ„ K еҖје°ҸдәҺзңҹе®һзҡ„з°Үзҡ„ж•°зӣ®ж—¶пјҢиҝҷдёӘжҢҮж ҮдёҖе®ҡдјҡжҖҘеү§дёҠеҚҮгҖӮ
ж №жҚ®иҝҷж ·зҡ„дј°з®—жҖқжғіпјҢжҲ‘们е°ұиғҪдј°и®ЎеҮәжӯЈзЎ®зҡ„ k еҖјпјҢ并且еҫ—еҲ° k дёӘеҲқе§ӢиҙЁеҝғпјҢжҺҘзқҖпјҢжҲ‘们дҫҝж №жҚ®дёҠиҝ°з®—жі•жөҒзЁӢ继з»ӯиҝӣиЎҢиҝӯд»ЈпјҢзӣҙеҲ°жүҖжңүиҙЁеҝғйғҪдёҚеҸҳеҢ–пјҢд»ҺиҖҢжҲҗеҠҹе®һзҺ°з®—жі•гҖӮеҰӮдёӢеӣҫжүҖзӨәпјҡ
еӣҫ 1. K еҖјдј°и®Ў
жҲ‘们зҹҘйҒ“ k еқҮеҖјжҖ»жҳҜ收ж•ӣзҡ„пјҢд№ҹе°ұжҳҜиҜҙпјҢk еқҮеҖјз®—жі•дёҖе®ҡдјҡиҫҫеҲ°дёҖз§ҚзЁіе®ҡзҠ¶жҖҒпјҢеңЁжӯӨзҠ¶жҖҒдёӢпјҢжүҖжңүзҡ„зӮ№йғҪдёҚдјҡд»ҺдёҖдёӘз°ҮиҪ¬з§»еҲ°еҸҰдёҖдёӘз°ҮпјҢеӣ жӯӨиҙЁеҝғдёҚеңЁеҸ‘з”ҹж”№еҸҳгҖӮеңЁжӯӨпјҢжҲ‘们引еҮәдёҖдёӘеүӘжһқдјҳеҢ–пјҢеҚіпјҡk еқҮеҖјжңҖжҳҺжҳҫзҡ„收ж•ӣиҝҮзЁӢдјҡеҸ‘з”ҹеңЁз®—жі•иҝҗиЎҢзҡ„еүҚжңҹйҳ¶ж®өпјҢж•…еңЁжҹҗдәӣжғ…еҶөдёӢдёәдәҶеўһеҠ з®—жі•зҡ„жү§иЎҢж•ҲзҺҮпјҢжҲ‘们еҸҜд»ҘжӣҝжҚўдёҠиҝ°з®—жі•зҡ„第дә”жӯҘпјҢйҮҮз”Ё“иҝӯд»ЈиҮід»…жңү 1%~3%зҡ„зӮ№еңЁеҪұе“ҚиҙЁеҝғ”жҲ–“иҝӯд»ЈиҮід»…жңү 1%~3%зҡ„зӮ№еңЁж”№еҸҳз°Ү”гҖӮ
k еқҮеҖјйҖӮз”ЁдәҺз»қеӨ§еӨҡж•°зҡ„ж•°жҚ®зұ»еһӢпјҢ并且з®ҖеҚ•жңүж•ҲгҖӮдҪҶе…¶зјәзӮ№е°ұжҳҜйңҖиҰҒзҹҘйҒ“еҮҶзЎ®зҡ„ k еҖјпјҢ并且дёҚиғҪеӨ„зҗҶејӮеҪўз°ҮпјҢжҜ”еҰӮзҗғеҪўз°ҮпјҢдёҚеҗҢе°әеҜёеҸҠеҜҶеәҰзҡ„з°ҮпјҢзҺҜеҪўз°ҮзӯүзӯүгҖӮ
жң¬ж–Үдё»иҰҒдёәз®—жі•и®Іи§ЈеҸҠе®һзҺ°пјҢеӣ жӯӨд»Јз Ғе®һзҺ°жҡӮдёҚиҖғиҷ‘йқўеҗ‘еҜ№иұЎжҖқжғіпјҢйҮҮз”Ёйқўеҗ‘иҝҮзЁӢзҡ„е®һзҺ°ж–№ејҸпјҢеҰӮжһңж•°жҚ®еӨҡз»ҙпјҢеҸҜиғҪдјҡйңҖиҰҒеҒҡж•°жҚ®йў„еӨ„зҗҶпјҢжҜ”еҰӮеҪ’дёҖеҢ–пјҢ并且дҝ®ж”№д»Јз Ғзӣёе…іж–№жі•еҚіеҸҜгҖӮ
з®—жі•е®һзҺ°
жё…еҚ• 1. Kmeans з®—жі•д»Јз Ғе®һзҺ°
import java.io.BufferedReader;
import java.io.FileReader;
import java.io.IOException;
import java.io.PrintStream;
import java.text.DecimalFormat;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Queue;
public class Kmeans {
private class Node {
int label;// label з”ЁжқҘи®°еҪ•зӮ№еұһдәҺ第еҮ дёӘ cluster
doubleпј»пјҪ attributes;
public NodeпјҲпјү {
attributes = new doubleпј»100пјҪ;
}
}
private class NodeComparator {
Node nodeOne;
Node nodeTwo;
double distance;
public void computeпјҲпјү {
double val = 0;
for пјҲint i = 0; i гҖҠ dimension; ++iпјү {
val += пјҲthis.nodeOne.attributesпј»iпјҪ - this.nodeTwo.attributesпј»iпјҪпјү *
пјҲthis.nodeOne.attributesпј»iпјҪ - this.nodeTwo.attributesпј»iпјҪпјү;
}
this.distance = val;
}
}
private ArrayListгҖҠNodeгҖӢ arraylist;
private ArrayListгҖҠNodeгҖӢ centroidList;
private double averageDis;
private int dimension;
private QueueгҖҠNodeComparatorгҖӢ FsQueue =
new PriorityQueueгҖҠNodeComparatorгҖӢпјҲ150пјҢ // з”ЁжқҘжҺ’еәҸд»»ж„ҸдёӨзӮ№д№Ӣй—ҙзҡ„и·қзҰ»пјҢд»ҺеӨ§еҲ°е°ҸжҺ’
new ComparatorгҖҠNodeComparatorгҖӢпјҲпјү {
public int compareпјҲNodeComparator oneпјҢ NodeComparator twoпјү {
if пјҲone.distance гҖҠ two.distanceпјү
return 1;
else if пјҲone.distance гҖӢ two.distanceпјү
return -1;
else
return 0;
}
}пјү;
public void setKmeansInputпјҲString pathпјү {
try {
BufferedReader br = new BufferedReaderпјҲnew FileReaderпјҲpathпјүпјү;
String str;
Stringпј»пјҪ strArray;
arraylist = new ArrayListгҖҠNodeгҖӢпјҲпјү;
while пјҲпјҲstr = br.readLineпјҲпјүпјү пјҒ= nullпјү {
strArray = str.splitпјҲ“пјҢ”пјү;
dimension = strArray.length;
Node node = new NodeпјҲпјү;
for пјҲint i = 0; i гҖҠ dimension; ++iпјү {
node.attributesпј»iпјҪ = Double.parseDoubleпјҲstrArrayпј»iпјҪпјү;
}
arraylist.addпјҲnodeпјү;
}
br.closeпјҲпјү;
} catch пјҲIOException eпјү {
e.printStackTraceпјҲпјү;
}
}
public void computeTheKпјҲпјү {
int cntTuple = 0;
for пјҲint i = 0; i гҖҠ arraylist.sizeпјҲпјү - 1; ++iпјү {
for пјҲint j = i + 1; j гҖҠ arraylist.sizeпјҲпјү; ++jпјү {
NodeComparator nodecomp = new NodeComparatorпјҲпјү;
nodecomp.nodeOne = new NodeпјҲпјү;
nodecomp.nodeTwo = new NodeпјҲпјү;
for пјҲint k = 0; k гҖҠ dimension; ++kпјү {
nodecomp.nodeOne.attributesпј»kпјҪ = arraylist.getпјҲiпјү.attributesпј»kпјҪ;
nodecomp.nodeTwo.attributesпј»kпјҪ = arraylist.getпјҲjпјү.attributesпј»kпјҪ;
}
nodecomp.computeпјҲпјү;
averageDis += nodecomp.distance;
FsQueue.addпјҲnodecompпјү;
cntTuple++;
}
}
averageDis /= cntTuple;// и®Ўз®—е№іеқҮи·қзҰ»
chooseCentroidпјҲFsQueueпјү;
}
public double getDistanceпјҲNode oneпјҢ Node twoпјү {// и®Ўз®—дёӨзӮ№й—ҙзҡ„欧ж°Ҹи·қзҰ»
double val = 0;
for пјҲint i = 0; i гҖҠ dimension; ++iпјү {
val += пјҲone.attributesпј»iпјҪ - two.attributesпј»iпјҪпјү * пјҲone.attributesпј»iпјҪ - two.attributesпј»iпјҪпјү;
}
return val;
}
public void chooseCentroidпјҲQueueгҖҠNodeComparatorгҖӢ queueпјү {
centroidList = new ArrayListгҖҠNodeгҖӢпјҲпјү;
boolean flag = false;
while пјҲпјҒqueue.isEmptyпјҲпјүпјү {
boolean judgeOne = false;
boolean judgeTwo = false;
NodeComparator nc = FsQueue.pollпјҲпјү;
if пјҲnc.distance гҖҠ averageDisпјү
break;// еҰӮжһңжҺҘдёӢжқҘзҡ„е…ғз»„пјҢдёӨиҠӮзӮ№й—ҙи·қзҰ»е°ҸдәҺе№іеқҮи·қзҰ»пјҢеҲҷдёҚ继з»ӯиҝӯд»Ј
if пјҲпјҒflagпјү {
centroidList.addпјҲnc.nodeOneпјү;// е…ҲеҠ е…ҘжүҖжңүзӮ№дёӯи·қзҰ»жңҖиҝңзҡ„дёӨдёӘзӮ№
centroidList.addпјҲnc.nodeTwoпјү;
flag = true;
} else {// д№ӢеҗҺд»Һд№ӢеүҚе·ІеҠ е…Ҙзҡ„жңҖиҝңзҡ„дёӨдёӘзӮ№ејҖе§ӢпјҢжүҫзҰ»иҝҷдёӨдёӘзӮ№жңҖиҝңзҡ„зӮ№пјҢ
// еҰӮжһңи·қзҰ»еӨ§дәҺжүҖжңүзӮ№зҡ„е№іеқҮи·қзҰ»пјҢеҲҷи®ӨдёәжүҫеҲ°дәҶж–°зҡ„иҙЁеҝғпјҢеҗҰеҲҷдёҚи®Өе®ҡдёәиҙЁеҝғ
for пјҲint i = 0; i гҖҠ centroidList.sizeпјҲпјү; ++iпјү {
Node testnode = centroidList.getпјҲiпјү;
if пјҲcentroidList.containsпјҲnc.nodeOneпјү || getDistanceпјҲtestnodeпјҢ nc.nodeOneпјү гҖҠ averageDisпјү {
judgeOne = true;
}
if пјҲcentroidList.containsпјҲnc.nodeTwoпјү || getDistanceпјҲtestnodeпјҢ nc.nodeTwoпјү гҖҠ averageDisпјү {
judgeTwo = true;
}
}
if пјҲпјҒjudgeOneпјү {
centroidList.addпјҲnc.nodeOneпјү;
}
if пјҲпјҒjudgeTwoпјү {
centroidList.addпјҲnc.nodeTwoпјү;
}
}
}
}
public void doIterationпјҲArrayListгҖҠNodeгҖӢ centroidпјү {
int cnt = 1;
int cntEnd = 0;
int numLabel = centroid.sizeпјҲпјү;
while пјҲtrueпјү {// иҝӯд»ЈпјҢзӣҙеҲ°жүҖжңүзҡ„иҙЁеҝғйғҪдёҚеҸҳеҢ–дёәжӯў
boolean flag = false;
for пјҲint i = 0; i гҖҠ arraylist.sizeпјҲпјү; ++iпјү {
double dis = 0x7fffffff;
cnt = 1;
for пјҲint j = 0; j гҖҠ centroid.sizeпјҲпјү; ++jпјү {
Node node = centroid.getпјҲjпјү;
if пјҲgetDistanceпјҲarraylist.getпјҲiпјүпјҢ nodeпјү гҖҠ disпјү {
dis = getDistanceпјҲarraylist.getпјҲiпјүпјҢ nodeпјү;
arraylist.getпјҲiпјү.label = cnt;
}
cnt++;
}
}
int j = 0;
numLabel -= 1;
while пјҲj гҖҠ numLabelпјү {
int c = 0;
Node node = new NodeпјҲпјү;
for пјҲint i = 0; i гҖҠ arraylist.sizeпјҲпјү; ++iпјү {
if пјҲarraylist.getпјҲiпјү.label == j + 1пјү {
for пјҲint k = 0; k гҖҠ dimension; ++kпјү {
node.attributesпј»kпјҪ += arraylist.getпјҲiпјү.attributesпј»kпјҪ;
}
c++;
}
}
DecimalFormat df = new DecimalFormatпјҲ“#.###”пјү;// дҝқз•ҷе°Ҹж•°зӮ№еҗҺдёүдҪҚ
doubleпј»пјҪ attributelist = new doubleпј»100пјҪ;
for пјҲint i = 0; i гҖҠ dimension; ++iпјү {
attributelistпј»iпјҪ = Double.parseDoubleпјҲdf.formatпјҲnode.attributesпј»iпјҪ / cпјүпјү;
if пјҲattributelistпј»iпјҪ пјҒ= centroid.getпјҲjпјү.attributesпј»iпјҪпјү {
centroid.getпјҲjпјү.attributesпј»iпјҪ = attributelistпј»iпјҪ;
flag = true;
}
}
if пјҲпјҒflagпјү {
cntEnd++;
if пјҲcntEnd == numLabelпјү {// иӢҘжүҖжңүзҡ„иҙЁеҝғйғҪдёҚеҸҳпјҢеҲҷи·іеҮәеҫӘзҺҜ
break;
}
}
j++;
}
if пјҲcntEnd == numLabelпјү {// иӢҘжүҖжңүзҡ„иҙЁеҝғйғҪдёҚеҸҳпјҢеҲҷ success
System.out.printlnпјҲ“run kmeans successfully.”пјү;
break;
}
}
}
public void printKmeansResultsпјҲString pathпјү {
try {
PrintStream out = new PrintStreamпјҲpathпјү;
computeTheKпјҲпјү;
doIterationпјҲcentroidListпјү;
out.printlnпјҲ“There are ” + centroidList.sizeпјҲпјү + “ clustersпјҒ”пјү;
for пјҲint i = 0; i гҖҠ arraylist.sizeпјҲпјү; ++iпјү {
out.printпјҲ“пјҲ”пјү;
for пјҲint j = 0; j гҖҠ dimension - 1; ++jпјү {
out.printпјҲarraylist.getпјҲiпјү.attributesпј»jпјҪ + “пјҢ ”пјү;
}
out.printпјҲarraylist.getпјҲiпјү.attributesпј»dimension - 1пјҪ + “пјү ”пјү;
out.printlnпјҲ“belongs to cluster ” + arraylist.getпјҲiпјү.labelпјү;
}
out.closeпјҲпјү;
System.out.printlnпјҲ“Please check results inпјҡ ” + pathпјү;
} catch пјҲIOException eпјү {
e.printStackTraceпјҲпјү;
}
}
public static void mainпјҲStringпј»пјҪ argsпјү {
Kmeans kmeans = new KmeansпјҲпјү;
kmeans.setKmeansInputпјҲ“c:/kmeans.txt”пјү;
kmeans.printKmeansResultsпјҲ“c:/kmeansResults.txt”пјү;
}
}
жөӢиҜ•ж•°жҚ®
з»ҷеҮәдёҖз»„з®ҖеҚ•зҡ„дәҢз»ҙжөӢиҜ•ж•°жҚ®пјҡ
жё…еҚ• 2. Kmeans з®—жі•жөӢиҜ•ж•°жҚ®
1пјҢ1
2пјҢ1
1пјҢ2
2пјҢ2
6пјҢ1
6пјҢ2
7пјҢ1
7пјҢ2
1пјҢ5
1пјҢ6
2пјҢ5
2пјҢ6
6пјҢ5
6пјҢ6
7пјҢ5
7пјҢ6
иҝҗиЎҢз»“жһң
жё…еҚ• 3. Kmeans з®—жі•иҝҗиЎҢз»“жһң
There are 4 clustersпјҒ
пјҲ1.0пјҢ 1.0пјү belongs to cluster 1
пјҲ2.0пјҢ 1.0пјү belongs to cluster 1
пјҲ1.0пјҢ 2.0пјү belongs to cluster 1
пјҲ2.0пјҢ 2.0пјү belongs to cluster 1
пјҲ6.0пјҢ 1.0пјү belongs to cluster 3
пјҲ6.0пјҢ 2.0пјү belongs to cluster 3
пјҲ7.0пјҢ 1.0пјү belongs to cluster 3
пјҲ7.0пјҢ 2.0пјү belongs to cluster 3
пјҲ1.0пјҢ 5.0пјү belongs to cluster 4
пјҲ1.0пјҢ 6.0пјү belongs to cluster 4
пјҲ2.0пјҢ 5.0пјү belongs to cluster 4
пјҲ2.0пјҢ 6.0пјү belongs to cluster 4
пјҲ6.0пјҢ 5.0пјү belongs to cluster 2
пјҲ6.0пјҢ 6.0пјү belongs to cluster 2
пјҲ7.0пјҢ 5.0пјү belongs to cluster 2
пјҲ7.0пјҢ 6.0пјү belongs to cluster 2
еұӮж¬ЎиҒҡзұ»з®—жі•иҜҰи§ЈеҸҠе®һзҺ°
еұӮж¬ЎиҒҡзұ»з®Җд»Ӣ
еұӮж¬ЎиҒҡзұ»еҲҶдёәеҮқиҒҡејҸеұӮж¬ЎиҒҡзұ»е’ҢеҲҶиЈӮејҸеұӮж¬ЎиҒҡзұ»гҖӮ
еҮқиҒҡејҸеұӮж¬ЎиҒҡзұ»пјҢе°ұжҳҜеңЁеҲқе§Ӣйҳ¶ж®өе°ҶжҜҸдёҖдёӘзӮ№йғҪи§ҶдёәдёҖдёӘз°ҮпјҢд№ӢеҗҺжҜҸдёҖж¬ЎеҗҲ并дёӨдёӘжңҖжҺҘиҝ‘зҡ„з°ҮпјҢеҪ“然еҜ№дәҺжҺҘиҝ‘зЁӢеәҰзҡ„е®ҡд№үеҲҷйңҖиҰҒжҢҮе®ҡз°Үзҡ„йӮ»иҝ‘еҮҶеҲҷгҖӮ
еҲҶиЈӮејҸеұӮж¬ЎиҒҡзұ»пјҢе°ұжҳҜеңЁеҲқе§Ӣйҳ¶ж®өе°ҶжүҖжңүзҡ„зӮ№и§ҶдёәдёҖдёӘз°ҮпјҢд№ӢеҗҺжҜҸж¬ЎеҲҶиЈӮеҮәдёҖдёӘз°ҮпјҢзӣҙеҲ°жңҖеҗҺеү©дёӢеҚ•дёӘзӮ№зҡ„з°ҮдёәжӯўгҖӮ
жң¬ж–ҮдёӯжҲ‘们е°ҶиҜҰз»Ҷд»Ӣз»ҚеҮқиҒҡејҸеұӮж¬ЎиҒҡзұ»з®—жі•гҖӮ
еҜ№дәҺеҮқиҒҡејҸеұӮж¬ЎиҒҡзұ»пјҢжҢҮе®ҡз°Үзҡ„йӮ»иҝ‘еҮҶеҲҷжҳҜйқһеёёйҮҚиҰҒзҡ„дёҖдёӘзҺҜиҠӮпјҢеңЁжӯӨжҲ‘们д»Ӣз»Қдёүз§ҚжңҖеёёз”Ёзҡ„еҮҶеҲҷпјҢеҲҶеҲ«жҳҜ MAXпјҢ MINпјҢ з»„е№іеқҮгҖӮеҰӮдёӢеӣҫжүҖзӨәпјҡ
еӣҫ 2. еұӮж¬ЎиҒҡзұ»и®Ўз®—еҮҶеҲҷ
еҮқиҒҡејҸеұӮж¬ЎиҒҡзұ»з®—жі•д№ҹжҳҜдёҖдёӘиҝӯд»Јзҡ„иҝҮзЁӢпјҢз®—жі•жөҒзЁӢеҰӮдёӢпјҡ
жҜҸж¬ЎйҖүжңҖиҝ‘зҡ„дёӨдёӘз°ҮеҗҲ并пјҢжҲ‘们е°ҶиҝҷдёӨдёӘеҗҲ并еҗҺзҡ„з°Үз§°д№ӢдёәеҗҲ并з°ҮгҖӮ
иӢҘйҮҮз”Ё MAX еҮҶеҲҷпјҢйҖүжӢ©е…¶д»–з°ҮдёҺеҗҲ并з°ҮдёӯзҰ»еҫ—жңҖиҝңзҡ„дёӨдёӘзӮ№д№Ӣй—ҙзҡ„и·қзҰ»дҪңдёәз°Үд№Ӣй—ҙзҡ„йӮ»иҝ‘еәҰгҖӮиӢҘйҮҮз”Ё MIN еҮҶеҲҷпјҢеҸ–е…¶д»–з°ҮдёҺеҗҲ并з°ҮдёӯзҰ»еҫ—жңҖиҝ‘зҡ„дёӨдёӘзӮ№д№Ӣй—ҙзҡ„и·қзҰ»дҪңдёәз°Үд№Ӣй—ҙзҡ„йӮ»иҝ‘еәҰгҖӮиӢҘз»„е№іеқҮеҮҶеҲҷпјҢеҸ–е…¶д»–з°ҮдёҺеҗҲ并з°ҮжүҖжңүзӮ№д№Ӣй—ҙи·қзҰ»зҡ„е№іеқҮеҖјдҪңдёәз°Үд№Ӣй—ҙзҡ„йӮ»иҝ‘еәҰгҖӮ
йҮҚеӨҚжӯҘйӘӨ 1 е’ҢжӯҘйӘӨ 2пјҢеҗҲ并иҮіеҸӘеү©дёӢдёҖдёӘз°ҮгҖӮ
з®—жі•иҝҮзЁӢдёҫдҫӢ
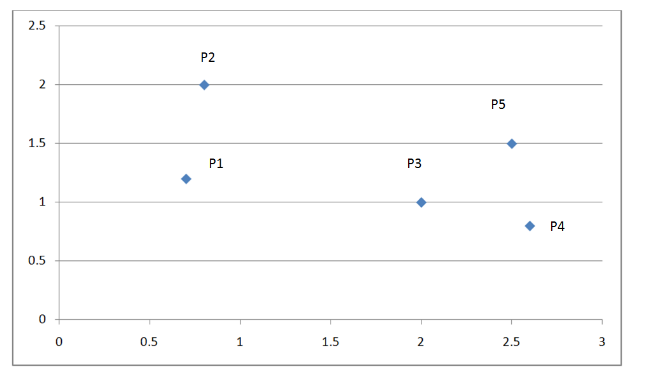
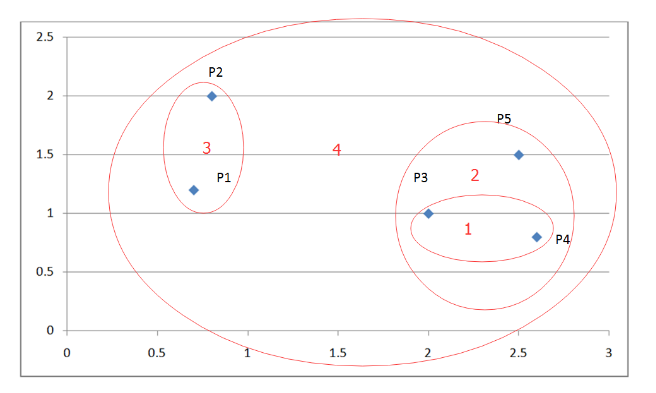
дёӢйқўжҲ‘们зңӢдёҖдёӘдҫӢеӯҗпјҡ
дёӢеӣҫжҳҜдёҖдёӘжңүдә”дёӘзӮ№зҡ„иҖҢдёәеқҗж Үзі»пјҡ
еӣҫ 3. еұӮж¬ЎиҒҡзұ»дёҫдҫӢ
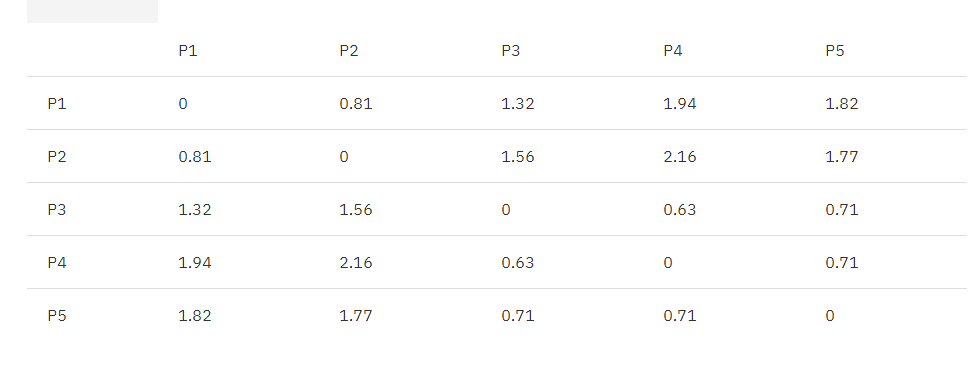
дёӢиЎЁдёәиҝҷдә”дёӘзӮ№зҡ„欧ејҸи·қзҰ»зҹ©йҳөпјҡ
иЎЁ 1. 欧ејҸи·қзҰ»еҺҹе§Ӣзҹ©йҳө
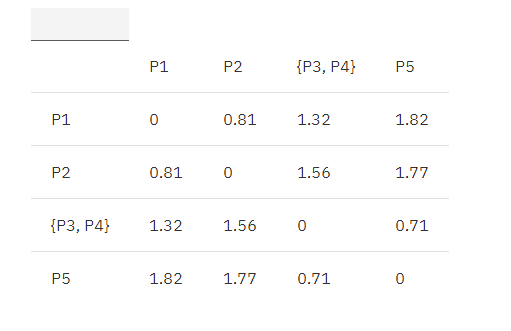
ж №жҚ®з®—жі•жөҒзЁӢпјҢжҲ‘们е…ҲжүҫеҮәи·қзҰ»жңҖиҝ‘зҡ„дёӨдёӘз°ҮпјҢP3пјҢ P4гҖӮ
еҗҲ并 P3пјҢ P4 дёә {P3пјҢ P4}пјҢж №жҚ® MIN еҺҹеҲҷжӣҙж–°зҹ©йҳөеҰӮдёӢпјҡ
MIN.distanceпјҲ{P3пјҢ P4}пјҢ P1пјү = 1.32;
MIN.distanceпјҲ{P3пјҢ P4}пјҢ P2пјү = 1.56;
MIN.distanceпјҲ{P3пјҢ P4}пјҢ P5пјү = 0.70;
иЎЁ 2. 欧ејҸи·қзҰ»жӣҙж–°зҹ©йҳө 1
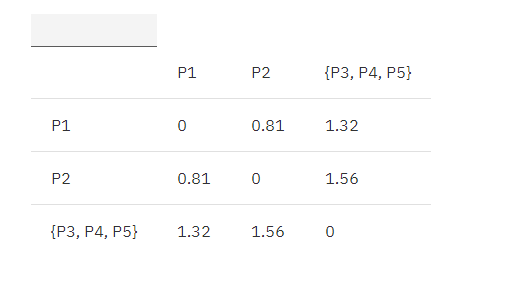
жҺҘзқҖ继з»ӯжүҫеҮәи·қзҰ»жңҖиҝ‘зҡ„дёӨдёӘз°ҮпјҢ{P3пјҢ P4}пјҢ P5гҖӮ
еҗҲ并 {P3пјҢ P4}пјҢ P5 дёә {P3пјҢ P4пјҢ P5}пјҢж №жҚ® MIN еҺҹеҲҷ继з»ӯжӣҙж–°зҹ©йҳөпјҡ
MIN.distanceпјҲP1пјҢ {P3пјҢ P4пјҢ P5}пјү = 1.32;
MIN.distanceпјҲP2пјҢ {P3пјҢ P4пјҢ P5}пјү = 1.56;
иЎЁ 3. 欧ејҸи·қзҰ»жӣҙж–°зҹ©йҳө 2
жҺҘзқҖ继з»ӯжүҫеҮәи·қзҰ»жңҖиҝ‘зҡ„дёӨдёӘз°ҮпјҢP1пјҢ P2гҖӮ
еҗҲ并 P1пјҢ P2 дёә {P1пјҢ P2}пјҢж №жҚ® MIN еҺҹеҲҷ继з»ӯжӣҙж–°зҹ©йҳөпјҡ
MIN.distanceпјҲ{P1пјҢP2}пјҢ {P3пјҢ P4пјҢ P5}пјү = 1.32
иЎЁ 4. 欧ејҸи·қзҰ»жӣҙж–°зҹ©йҳө 3
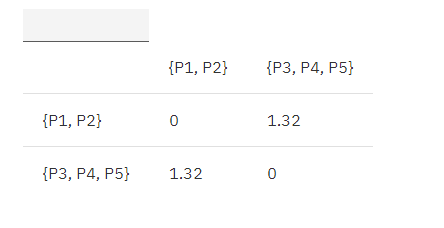
жңҖз»ҲеҗҲ并еү©дёӢзҡ„иҝҷдёӨдёӘз°ҮеҚіеҸҜиҺ·еҫ—жңҖз»Ҳз»“жһңпјҢеҰӮдёӢеӣҫпјҡ
еӣҫ 4. еұӮж¬ЎиҒҡзұ»дёҫдҫӢз»“жһң
MAXпјҢз»„е№іеқҮз®—жі•жөҒзЁӢеҗҢзҗҶпјҢеҸӘжҳҜеңЁжӣҙж–°зҹ©йҳөж—¶е°ҶдёҠиҝ°и®Ўз®—з°Үй—ҙи·қзҰ»еҸҳдёәз°Үй—ҙдёӨзӮ№жңҖеӨ§ж¬§ејҸи·қзҰ»пјҢе’Ңз°Үй—ҙжүҖжңүзӮ№е№іеқҮ欧ејҸи·қзҰ»еҚіеҸҜгҖӮ
з®—жі•е®һзҺ°
жё…еҚ• 4. еұӮж¬ЎиҒҡзұ»з®—жі•д»Јз Ғе®һзҺ°
import java.io.BufferedReader;
import java.io.FileReader;
import java.io.IOException;
import java.io.PrintStream;
import java.text.DecimalFormat;
import java.util.ArrayList;
public class Hierarchical {
private doubleпј»пјҪпј»пјҪ matrix;
private int dimension;// ж•°жҚ®з»ҙеәҰ
private class Node {
doubleпј»пјҪ attributes;
public NodeпјҲпјү {
attributes = new doubleпј»100пјҪ;
}
}
private ArrayListгҖҠNodeгҖӢ arraylist;
private class Model {
int x = 0;
int y = 0;
double value = 0;
}
private Model minModel = new ModelпјҲпјү;
private double getDistanceпјҲNode oneпјҢ Node twoпјү {// и®Ўз®—дёӨзӮ№й—ҙзҡ„欧ж°Ҹи·қзҰ»
double val = 0;
for пјҲint i = 0; i гҖҠ dimension; ++iпјү {
val += пјҲone.attributesпј»iпјҪ - two.attributesпј»iпјҪпјү * пјҲone.attributesпј»iпјҪ - two.attributesпј»iпјҪпјү;
}
return Math.sqrtпјҲvalпјү;
}
private void loadMatrixпјҲпјү {// е°Ҷиҫ“е…Ҙж•°жҚ®иҪ¬еҢ–дёәзҹ©йҳө
for пјҲint i = 0; i гҖҠ matrix.length; ++iпјү {
for пјҲint j = i + 1; j гҖҠ matrix.length; ++jпјү {
double distance = getDistanceпјҲarraylist.getпјҲiпјүпјҢ arraylist.getпјҲjпјүпјү;
matrixпј»iпјҪпј»jпјҪ = distance;
}
}
}
private Model findMinValueOfMatrixпјҲdoubleпј»пјҪпј»пјҪ matrixпјү {// жүҫеҮәзҹ©йҳөдёӯи·қзҰ»жңҖиҝ‘зҡ„дёӨдёӘз°Ү
Model model = new ModelпјҲпјү;
double min = 0x7fffffff;
for пјҲint i = 0; i гҖҠ matrix.length; ++iпјү {
for пјҲint j = i + 1; j гҖҠ matrix.length; ++jпјү {
if пјҲmin гҖӢ matrixпј»iпјҪпј»jпјҪ && matrixпј»iпјҪпј»jпјҪ пјҒ= 0пјү {
min = matrixпј»iпјҪпј»jпјҪ;
model.x = i;
model.y = j;
model.value = matrixпј»iпјҪпј»jпјҪ;
}
}
}
return model;
}
private void processHierarchicalпјҲString pathпјү {
try {
PrintStream out = new PrintStreamпјҲpathпјү;
while пјҲtrueпјү {// еҮқиҒҡеұӮж¬ЎиҒҡзұ»иҝӯд»Ј
out.printlnпјҲ“Matrix update as belowпјҡ ”пјү;
for пјҲint i = 0; i гҖҠ matrix.length; ++iпјү {// иҫ“еҮәжҜҸж¬Ўиҝӯд»Јжӣҙж–°зҡ„зҹ©йҳө
for пјҲint j = 0; j гҖҠ matrix.length - 1; ++jпјү {
out.printпјҲnew DecimalFormatпјҲ“#.00”пјү.formatпјҲmatrixпј»iпјҪпј»jпјҪпјү + “ ”пјү;
}
out.printlnпјҲnew DecimalFormatпјҲ“#.00”пјү.formatпјҲmatrixпј»iпјҪпј»matrix.length - 1пјҪпјүпјү;
}
out.printlnпјҲпјү;
minModel = findMinValueOfMatrixпјҲmatrixпјү;
if пјҲminModel.value == 0пјү {// еҪ“жүҫдёҚеҮәи·қзҰ»жңҖиҝ‘зҡ„дёӨдёӘз°Үж—¶пјҢиҝӯд»Јз»“жқҹ
break;
}
out.printlnпјҲ“Combine ” + пјҲminModel.x + 1пјү + “ ” + пјҲminModel.y + 1пјүпјү;
out.printlnпјҲ“The distance isпјҡ ” + minModel.valueпјү;
matrixпј»minModel.xпјҪпј»minModel.yпјҪ = 0;// жӣҙж–°зҹ©йҳө
for пјҲint i = 0; i гҖҠ matrix.length; ++iпјү {// еҰӮжһңеҗҲ并дәҶзӮ№ p1 дёҺ p2пјҢеҲҷеҸӘдҝқз•ҷ p1пјҢp2 е…¶дёӯд№ӢдёҖдёҺе…¶д»–зӮ№зҡ„и·қзҰ»пјҢеҸ–иҫғе°ҸеҖј
if пјҲmatrixпј»iпјҪпј»minModel.xпјҪ гҖҠ= matrixпј»iпјҪпј»minModel.yпјҪпјү {
matrixпј»iпјҪпј»minModel.yпјҪ = 0;
} else {
matrixпј»iпјҪпј»minModel.xпјҪ = 0;
}
if пјҲmatrixпј»minModel.xпјҪпј»iпјҪ гҖҠ= matrixпј»minModel.yпјҪпј»iпјҪпјү {
matrixпј»minModel.yпјҪпј»iпјҪ = 0;
} else {
matrixпј»minModel.xпјҪпј»iпјҪ = 0;
}
}
}
out.closeпјҲпјү;
System.out.printlnпјҲ“Please check results inпјҡ ” + pathпјү;
} catch пјҲException eпјү {
e.printStackTraceпјҲпјү;
}
}
public void setInputпјҲString pathпјү {
try {
BufferedReader br = new BufferedReaderпјҲnew FileReaderпјҲpathпјүпјү;
String str;
Stringпј»пјҪ strArray;
arraylist = new ArrayListгҖҠNodeгҖӢпјҲпјү;
while пјҲпјҲstr = br.readLineпјҲпјүпјү пјҒ= nullпјү {
strArray = str.splitпјҲ“пјҢ”пјү;
dimension = strArray.length;
Node node = new NodeпјҲпјү;
for пјҲint i = 0; i гҖҠ dimension; ++iпјү {
node.attributesпј»iпјҪ = Double.parseDoubleпјҲstrArrayпј»iпјҪпјү;
}
arraylist.addпјҲnodeпјү;
}
matrix = new doubleпј»arraylist.sizeпјҲпјүпјҪпј»arraylist.sizeпјҲпјүпјҪ;
loadMatrixпјҲпјү;
br.closeпјҲпјү;
} catch пјҲIOException eпјү {
e.printStackTraceпјҲпјү;
}
}
public void printOutputпјҲString pathпјү {
processHierarchicalпјҲpathпјү;
}
public static void mainпјҲStringпј»пјҪ argsпјү {
Hierarchical hi = new HierarchicalпјҲпјү;
hi.setInputпјҲ“c:/hierarchical.txt”пјү;
hi.printOutputпјҲ“c:/hierarchical_results.txt”пјү;
}
}
жөӢиҜ•ж•°жҚ®
з»ҷеҮәдёҖз»„з®ҖеҚ•зҡ„дәҢз»ҙжөӢиҜ•ж•°жҚ®
жё…еҚ• 5. еұӮж¬ЎиҒҡзұ»з®—жі•жөӢиҜ•ж•°жҚ®
0.7пјҢ1.2
0.8пјҢ2
2пјҢ1
2.6пјҢ0.8
2.5пјҢ1.5
иҝҗиЎҢз»“жһң
жё…еҚ• 6. еұӮж¬ЎиҒҡзұ»з®—жі•иҝҗиЎҢз»“жһң
Matrix update as belowпјҡ
.00 .81 1.32 1.94 1.82
.00 .00 1.56 2.16 1.77
.00 .00 .00 .63 .71
.00 .00 .00 .00 .71
.00 .00 .00 .00 .00
Combine 3 4
The distance isпјҡ 0.6324555320336759
Matrix update as belowпјҡ
.00 .81 1.32 .00 1.82
.00 .00 1.56 .00 1.77
.00 .00 .00 .00 .00
.00 .00 .00 .00 .71
.00 .00 .00 .00 .00
Combine 4 5
The distance isпјҡ 0.7071067811865475
Matrix update as belowпјҡ
.00 .81 1.32 .00 .00
.00 .00 1.56 .00 .00
.00 .00 .00 .00 .00
.00 .00 .00 .00 .00
.00 .00 .00 .00 .00
Combine 1 2
The distance isпјҡ 0.806225774829855
Matrix update as belowпјҡ
.00 .00 1.32 .00 .00
.00 .00 .00 .00 .00
.00 .00 .00 .00 .00
.00 .00 .00 .00 .00
.00 .00 .00 .00 .00
Combine 1 3
The distance isпјҡ 1.3152946437965907
Matrix update as belowпјҡ
.00 .00 .00 .00 .00
.00 .00 .00 .00 .00
.00 .00 .00 .00 .00
.00 .00 .00 .00 .00
.00 .00 .00 .00 .00
DBSCAN з®—жі•иҜҰи§ЈеҸҠе®һзҺ°
иҖғиҷ‘дёҖз§Қжғ…еҶөпјҢзӮ№зҡ„еҲҶеёғдёҚеқҮеҢҖпјҢеҪўзҠ¶дёҚ规еҲҷж—¶пјҢKmeans з®—жі•еҸҠеұӮж¬ЎиҒҡзұ»з®—жі•е°ҶйқўдёҙеӨұж•Ҳзҡ„йЈҺйҷ©гҖӮ
еҰӮдёӢеқҗж Үзі»пјҡ
еӣҫ 5. DBSCAN з®—жі•дёҫдҫӢ
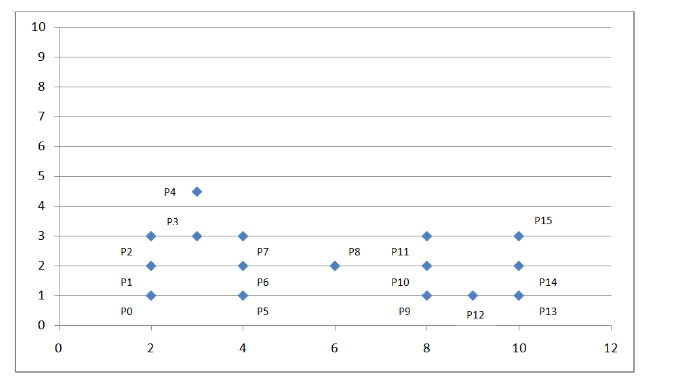
жҲ‘们еҸҜд»ҘзңӢеҲ°дёҠйқўзҡ„зӮ№еҜҶеәҰдёҚеқҮеҢҖпјҢиҝҷж—¶жҲ‘们иҖғиҷ‘йҮҮз”ЁеҹәдәҺеҜҶеәҰзҡ„иҒҡзұ»з®—жі•пјҡDBSCANгҖӮ
з®—жі•жөҒзЁӢ
и®ҫе®ҡжү«жҸҸеҚҠеҫ„ EpsпјҢ 并规е®ҡжү«жҸҸеҚҠеҫ„еҶ…зҡ„еҜҶеәҰеҖјгҖӮиӢҘеҪ“еүҚзӮ№зҡ„еҚҠеҫ„иҢғеӣҙеҶ…еҜҶеәҰеӨ§дәҺзӯүдәҺи®ҫе®ҡеҜҶеәҰеҖјпјҢеҲҷи®ҫзҪ®еҪ“еүҚзӮ№дёәж ёеҝғзӮ№пјӣиӢҘжҹҗзӮ№еҲҡеҘҪеңЁжҹҗж ёеҝғзӮ№зҡ„еҚҠеҫ„иҫ№зјҳдёҠпјҢеҲҷи®ҫе®ҡжӯӨзӮ№дёәиҫ№з•ҢзӮ№пјӣиӢҘжҹҗзӮ№ж—ўдёҚжҳҜж ёеҝғзӮ№еҸҲдёҚжҳҜиҫ№з•ҢзӮ№пјҢеҲҷжӯӨзӮ№дёәеҷӘеЈ°зӮ№гҖӮ
еҲ йҷӨеҷӘеЈ°зӮ№гҖӮ
е°Ҷи·қзҰ»еңЁжү«жҸҸеҚҠеҫ„еҶ…зҡ„жүҖжңүж ёеҝғзӮ№иөӢдәҲиҫ№иҝӣиЎҢиҝһйҖҡгҖӮ
жҜҸз»„иҝһйҖҡзҡ„ж ёеҝғзӮ№ж Үи®°дёәдёҖдёӘз°ҮгҖӮ
е°ҶжүҖжңүиҫ№з•ҢзӮ№жҢҮе®ҡеҲ°дёҺд№ӢеҜ№еә”зҡ„ж ёеҝғзӮ№зҡ„з°ҮжҖ»гҖӮ
з®—жі•иҝҮзЁӢдёҫдҫӢ
еҰӮдёҠеӣҫеқҗж Үзі»жүҖзӨәпјҢжҲ‘们и®ҫе®ҡжү«жҸҸеҚҠеҫ„ Eps дёә 1.5пјҢеҜҶеәҰйҳҲеҖј threshold дёә 3пјҢеҲҷйҖҡиҝҮдёҠиҝ°з®—жі•иҝҮзЁӢпјҢжҲ‘们еҸҜд»Ҙеҫ—еҲ°дёӢеӣҫпјҡ
еӣҫ 6. DBSCAN з®—жі•дёҫдҫӢз»“жһңзӨәдҫӢ
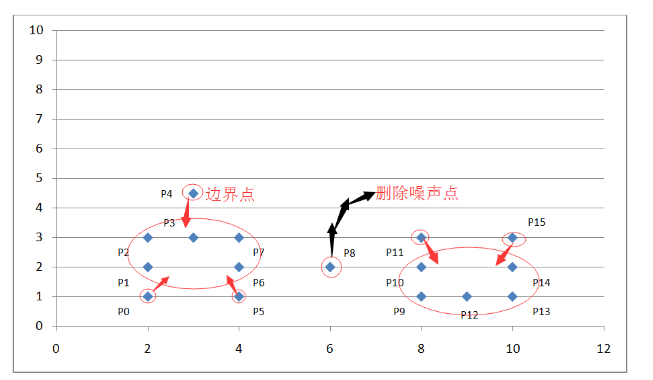
йҖҡиҝҮи®Ўз®—еҗ„дёӘзӮ№д№Ӣй—ҙзҡ„欧ејҸи·қзҰ»еҸҠе…¶жүҖеңЁжү«жҸҸеҚҠеҫ„еҶ…зҡ„еҜҶеәҰеҖјжқҘеҲӨж–ӯиҝҷдәӣзӮ№еұһдәҺж ёеҝғзӮ№пјҢиҫ№з•ҢзӮ№жҲ–жҳҜеҷӘеЈ°зӮ№гҖӮеӣ дёәжҲ‘们и®ҫе®ҡдәҶжү«жҸҸеҚҠеҫ„дёә 1.5пјҢеҜҶеәҰйҳҲеҖјдёә 3пјҢжүҖд»Ҙпјҡ
P0 зӮ№дёәиҫ№з•ҢзӮ№пјҢеӣ дёәеңЁд»Ҙе…¶дёәдёӯеҝғзҡ„жү«жҸҸеҚҠеҫ„еҶ…еҸӘжңүдёӨдёӘзӮ№ P0 е’Ң P1пјӣ
P1 зӮ№дёәж ёеҝғзӮ№пјҢеӣ дёәеңЁд»Ҙе…¶дёәдёӯеҝғзҡ„жү«жҸҸеҚҠеҫ„еҶ…жңүеӣӣдёӘзӮ№ P0пјҢP1пјҢP2пјҢP4 пјӣ
P8 дёәеҷӘеЈ°зӮ№пјҢеӣ дёәе…¶ж—ўйқһж ёеҝғзӮ№пјҢд№ҹйқһиҫ№з•ҢзӮ№пјӣ
е…¶д»–зӮ№дҫқж¬Ўзұ»жҺЁгҖӮ
з®—жі•е®һзҺ°
жё…еҚ• 7. DBSCAN з®—жі•д»Јз Ғе®һзҺ°
import java.io.BufferedReader;
import java.io.FileReader;
import java.io.IOException;
import java.io.PrintStream;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.Iterator;
import java.util.Map;
public class DBSCAN {
private int dimension;// ж•°жҚ®з»ҙеәҰ
private double eps = 1.5;
private int threshold = 3;
private double distanceпј»пјҪпј»пјҪ;
private MapгҖҠIntegerпјҢ IntegerгҖӢ id = new HashMapгҖҠIntegerпјҢ IntegerгҖӢпјҲпјү;
private int countClusters = 0;
private ArrayListгҖҠIntegerгҖӢ keyPointList = new ArrayListгҖҠIntegerгҖӢпјҲпјү;//
private intпј»пјҪ flags;// ж Үи®°иҫ№зјҳзӮ№
private class Edge {
int pпјҢ q;
double weight;
}
private class Node {
doubleпј»пјҪ attributes;
public NodeпјҲпјү {
attributes = new doubleпј»100пјҪ;
}
}
private ArrayListгҖҠNodeгҖӢ nodeList;
private ArrayListгҖҠEdgeгҖӢ edgeList;
private double getDistanceпјҲNode oneпјҢ Node twoпјү {// и®Ўз®—дёӨзӮ№й—ҙзҡ„欧ж°Ҹи·қзҰ»
double val = 0;
for пјҲint i = 0; i гҖҠ dimension; ++iпјү {
val += пјҲone.attributesпј»iпјҪ - two.attributesпј»iпјҪпјү * пјҲone.attributesпј»iпјҪ - two.attributesпј»iпјҪпјү;
}
return Math.sqrtпјҲvalпјү;
}
public void loadEdgesпјҲпјү {// з»ҷжүҖжңүеңЁжү«жҸҸеҚҠеҫ„еҶ…зҡ„ж ёеҝғзӮ№д№Ӣй—ҙеҠ иҫ№пјҢж Үи®°иҫ№з•ҢзӮ№е№¶дё”иҮӘеҠЁеҝҪз•ҘеҷӘеЈ°зӮ№
edgeList = new ArrayListгҖҠEdgeгҖӢпјҲпјү;
flags = new intпј»nodeList.sizeпјҲпјүпјҪ;
intпј»пјҪ countPoint = new intпј»nodeList.sizeпјҲпјүпјҪ;
for пјҲint i = 0; i гҖҠ countPoint.length; ++iпјү {
countPointпј»iпјҪ = 1;// жҜҸдёҖдёӘзӮ№дёҖејҖе§ӢйғҪжҳҜж ёеҝғзӮ№
}
for пјҲint i = 0; i гҖҠ nodeList.sizeпјҲпјү; ++iпјү {
for пјҲint j = i + 1; j гҖҠ nodeList.sizeпјҲпјү; ++jпјү {
distanceпј»iпјҪпј»jпјҪ = getDistanceпјҲnodeList.getпјҲiпјүпјҢ nodeList.getпјҲjпјүпјү;
if пјҲdistanceпј»iпјҪпј»jпјҪ гҖҠ= epsпјү {// дёӨзӮ№й—ҙи·қзҰ»е°ҸдәҺжү«жҸҸеҚҠеҫ„
countPointпј»iпјҪ++;
if пјҲcountPointпј»iпјҪ гҖӢ 0 && countPointпј»iпјҪ гҖҠ thresholdпјү {
flagsпј»iпјҪ = j;// и®°еҪ•иҫ№з•ҢзӮ№
}
if пјҲcountPointпј»iпјҪ гҖӢ= thresholdпјү {// еҰӮжһңи®°еҪ•еҪ“еүҚзӮ№зҡ„жү«жҸҸеҚҠеҫ„еҶ…еҜҶеәҰеҖјеӨ§дәҺжҲ–зӯүдәҺз»ҷе®ҡйҳҲеҖј
flagsпј»iпјҪ = 0;
if пјҲпјҒkeyPointList.containsпјҲiпјүпјү {
keyPointList.addпјҲiпјү;
}
}
countPointпј»jпјҪ++;
if пјҲcountPointпј»jпјҪ гҖӢ 0 && countPointпј»jпјҪ гҖҠ thresholdпјү {
flagsпј»jпјҪ = i;// и®°еҪ•иҫ№з•ҢзӮ№
}
if пјҲcountPointпј»jпјҪ гҖӢ= thresholdпјү {// еҰӮжһңи®°еҪ•еҪ“еүҚзӮ№зҡ„жү«жҸҸеҚҠеҫ„еҶ…еҜҶеәҰеҖјеӨ§дәҺжҲ–зӯүдәҺз»ҷе®ҡйҳҲеҖј
flagsпј»jпјҪ = 0;
if пјҲпјҒkeyPointList.containsпјҲjпјүпјү {
keyPointList.addпјҲjпјү;
}
}
}
}
}
for пјҲint i = 0; i гҖҠ keyPointList.sizeпјҲпјү; ++iпјү {
for пјҲint j = i + 1; j гҖҠ keyPointList.sizeпјҲпјү; ++jпјү {
Edge edge = new EdgeпјҲпјү;
edge.p = keyPointList.getпјҲiпјү;
edge.q = keyPointList.getпјҲjпјү;
edge.weight = distanceпј»edge.pпјҪпј»edge.qпјҪ;
if пјҲedge.weight гҖҠ= epsпјү {
if пјҲпјҒid.containsKeyпјҲedge.pпјүпјү {// дёәеҗҺжңҹдҪҝ用并жҹҘйӣҶжұӮиҝһйҖҡеҲҶйҮҸеҒҡеҮҶеӨҮ
id.putпјҲedge.pпјҢ edge.pпјү;
}
if пјҲпјҒid.containsKeyпјҲedge.qпјүпјү {
id.putпјҲedge.qпјҢ edge.qпјү;
}
edgeList.addпјҲedgeпјү;
}
}
}
}
public void setInputпјҲString pathпјү {
try {
BufferedReader br = new BufferedReaderпјҲnew FileReaderпјҲpathпјүпјү;
String str;
Stringпј»пјҪ strArray;
nodeList = new ArrayListгҖҠNodeгҖӢпјҲпјү;
while пјҲпјҲstr = br.readLineпјҲпјүпјү пјҒ= nullпјү {
strArray = str.splitпјҲ“пјҢ”пјү;
dimension = strArray.length;
Node node = new NodeпјҲпјү;
for пјҲint i = 0; i гҖҠ dimension; ++iпјү {
node.attributesпј»iпјҪ = Double.parseDoubleпјҲstrArrayпј»iпјҪпјү;
}
nodeList.addпјҲnodeпјү;
}
distance = new doubleпј»nodeList.sizeпјҲпјүпјҪпј»nodeList.sizeпјҲпјүпјҪ;
loadEdgesпјҲпјү;
br.closeпјҲпјү;
} catch пјҲIOException eпјү {
e.printStackTraceпјҲпјү;
}
}
public void unionпјҲint pпјҢ int qпјү {// 并ж“ҚдҪң
int a = findпјҲpпјү;
int b = findпјҲqпјү;
if пјҲa пјҒ= bпјү {
id.putпјҲaпјҢ bпјү;
}
}
public int findпјҲint pпјү {// жҹҘж“ҚдҪң
if пјҲp пјҒ= id.getпјҲpпјүпјү {
id.putпјҲpпјҢ findпјҲid.getпјҲpпјүпјүпјү;
}
return id.getпјҲpпјү;
}
public void processDBSCANпјҲString pathпјү {
try {
PrintStream out = new PrintStreamпјҲpathпјү;
out.printlnпјҲ“ж ёеҝғзӮ№дёәпјҡ ” + keyPointListпјү;
out.printlnпјҲпјү;
for пјҲint i = 0; i гҖҠ edgeList.sizeпјҲпјү; ++iпјү {
out.printlnпјҲ“ж ёеҝғзӮ№ пјҲ” + edgeList.getпјҲiпјү.p + “ ” +
edgeList.getпјҲiпјү.q + “пјү д№Ӣй—ҙзҡ„и·қзҰ»дёәпјҡ ” + edgeList.getпјҲiпјү.weightпјү;
}
for пјҲint i = 0; i гҖҠ edgeList.sizeпјҲпјү; ++iпјү {
unionпјҲedgeList.getпјҲiпјү.pпјҢ edgeList.getпјҲiпјү.qпјү;// еҲ©з”Ёе№¶жҹҘйӣҶе°ҶзӮ№йӣҶеҸҳдёәиҝһйҖҡеҲҶйҮҸ
}
IteratorгҖҠIntegerгҖӢ it = id.keySetпјҲпјү.iteratorпјҲпјү;
while пјҲit.hasNextпјҲпјүпјү {
int key = it.nextпјҲпјү;
if пјҲid.getпјҲkeyпјү == keyпјү {// еҲ©з”Ёе№¶жҹҘйӣҶеҫ—еҲ°ејәиҝһйҖҡеҲҶйҮҸдёӘж•°
++countClusters;
}
}
out.printlnпјҲпјү;
for пјҲint i = 0; i гҖҠ flags.length; ++iпјү {
if пјҲflagsпј»iпјҪ пјҒ= 0пјү {
out.printlnпјҲ“зӮ№” + i + “еұһдәҺзӮ№” + flagsпј»iпјҪ + “жүҖеңЁзҡ„з°Ү”пјү;
}
}
out.printlnпјҲпјү;
out.printlnпјҲ“з”ұж ёеҝғзӮ№иҝһйҖҡеҲҶйҮҸж•°йҮҸеҫ—зҹҘе…ұжңүпјҡ ” + countClusters + “дёӘз°Ү”пјү;
out.closeпјҲпјү;
System.out.printlnпјҲ“Please check results inпјҡ ” + pathпјү;
} catch пјҲException eпјү {
e.printStackTraceпјҲпјү;
}
}
public void printOutputпјҲString pathпјү {
processDBSCANпјҲpathпјү;
}
public static void mainпјҲStringпј»пјҪ argsпјү {
DBSCAN dbscan = new DBSCANпјҲпјү;
dbscan.setInputпјҲ“c:/dbscan.txt”пјү;
dbscan.printOutputпјҲ“c:/dbscan_results.txt”пјү;
}
}
жөӢиҜ•ж•°жҚ®
жё…еҚ• 8. DBSCAN з®—жі•жөӢиҜ•ж•°жҚ®
2пјҢ1
2пјҢ2
2пјҢ3
3пјҢ3
3пјҢ4.5
4пјҢ1
4пјҢ2
4пјҢ3
6пјҢ2
8пјҢ1
8пјҢ2
8пјҢ3
9пјҢ1
10пјҢ1
10пјҢ2
10пјҢ3
иҝҗиЎҢз»“жһң
жё…еҚ• 9. DBSCAN з®—жі•иҝҗиЎҢз»“жһң
ж ёеҝғзӮ№дёәпјҡ пј»1пјҢ 2пјҢ 3пјҢ 6пјҢ 7пјҢ 9пјҢ 10пјҢ 12пјҢ 13пјҢ 14пјҪ
ж ёеҝғзӮ№ пјҲ1 2пјү д№Ӣй—ҙзҡ„и·қзҰ»дёәпјҡ 1.0
ж ёеҝғзӮ№ пјҲ1 3пјү д№Ӣй—ҙзҡ„и·қзҰ»дёәпјҡ 1.4142135623730951
ж ёеҝғзӮ№ пјҲ2 3пјү д№Ӣй—ҙзҡ„и·қзҰ»дёәпјҡ 1.0
ж ёеҝғзӮ№ пјҲ3 6пјү д№Ӣй—ҙзҡ„и·қзҰ»дёәпјҡ 1.4142135623730951
ж ёеҝғзӮ№ пјҲ3 7пјү д№Ӣй—ҙзҡ„и·қзҰ»дёәпјҡ 1.0
ж ёеҝғзӮ№ пјҲ6 7пјү д№Ӣй—ҙзҡ„и·қзҰ»дёәпјҡ 1.0
ж ёеҝғзӮ№ пјҲ9 10пјү д№Ӣй—ҙзҡ„и·қзҰ»дёәпјҡ 1.0
ж ёеҝғзӮ№ пјҲ9 12пјү д№Ӣй—ҙзҡ„и·қзҰ»дёәпјҡ 1.0
ж ёеҝғзӮ№ пјҲ10 12пјү д№Ӣй—ҙзҡ„и·қзҰ»дёәпјҡ 1.4142135623730951
ж ёеҝғзӮ№ пјҲ12 13пјү д№Ӣй—ҙзҡ„и·қзҰ»дёәпјҡ 1.0
ж ёеҝғзӮ№ пјҲ12 14пјү д№Ӣй—ҙзҡ„и·қзҰ»дёәпјҡ 1.4142135623730951
ж ёеҝғзӮ№ пјҲ13 14пјү д№Ӣй—ҙзҡ„и·қзҰ»дёәпјҡ 1.0
иҝһйҖҡзӮ№ 1 е’ҢзӮ№ 2
иҝһйҖҡзӮ№ 1 е’ҢзӮ№ 3
иҝһйҖҡзӮ№ 3 е’ҢзӮ№ 6
иҝһйҖҡзӮ№ 3 е’ҢзӮ№ 7
иҝһйҖҡзӮ№ 9 е’ҢзӮ№ 10
иҝһйҖҡзӮ№ 9 е’ҢзӮ№ 12
иҝһйҖҡзӮ№ 12 е’ҢзӮ№ 13
иҝһйҖҡзӮ№ 12 е’ҢзӮ№ 14
зӮ№ 1гҖҒзӮ№ 2гҖҒзӮ№ 3гҖҒзӮ№ 6гҖҒзӮ№ 7 еҗҢеұһдәҺз°Ү 1
зӮ№ 9гҖҒзӮ№ 10гҖҒзӮ№ 12гҖҒзӮ№ 13гҖҒзӮ№ 14 еҗҢеұһдәҺз°Ү 2
зӮ№ 0 еұһдәҺзӮ№ 1 жүҖеңЁзҡ„з°Ү
зӮ№ 4 еұһдәҺзӮ№ 3 жүҖеңЁзҡ„з°Ү
зӮ№ 5 еұһдәҺзӮ№ 6 жүҖеңЁзҡ„з°Ү
зӮ№ 11 еұһдәҺзӮ№ 10 жүҖеңЁзҡ„з°Ү
зӮ№ 15 еұһдәҺзӮ№ 14 жүҖеңЁзҡ„з°Ү
з”ұж ёеҝғзӮ№иҝһйҖҡеҲҶйҮҸж•°йҮҸеҫ—зҹҘе…ұжңүпјҡ 2 дёӘз°Ү
е…¶д»–иҒҡзұ»з®—жі•з®Җд»Ӣ
BIRCH з®—жі•
Birch жҳҜдёҖз§ҚиғҪеӨҹй«ҳж•ҲеӨ„зҗҶеӨ§ж•°жҚ®иҒҡзұ»зҡ„еҹәдәҺж ‘зҡ„еұӮж¬ЎиҒҡзұ»з®—жі•гҖӮи®ҫжғіиҝҷж ·дёҖз§Қжғ…еҶөпјҢдёҖдёӘжӢҘжңүеӨ§и§„жЁЎж•°жҚ®зҡ„ж•°жҚ®еә“пјҢеҪ“иҝҷдәӣж•°жҚ®иў«ж”ҫе…Ҙдё»еӯҳиҝӣиЎҢиҒҡзұ»еӨ„зҗҶж—¶пјҢдёҖиҲ¬зҡ„иҒҡзұ»з®—жі•еҲҷжІЎжңүеҜ№еә”зҡ„й«ҳж•ҲеӨ„зҗҶиғҪеҠӣпјҢиҝҷж—¶ Birch з®—жі•жҳҜжңҖдҪізҡ„йҖүжӢ©гҖӮ
Birth дёҚд»…иғҪеӨҹй«ҳж•Ҳең°еӨ„зҗҶеӨ§ж•°жҚ®иҒҡзұ»пјҢ并且иғҪжңҖе°ҸеҢ– IO иҠұй”ҖгҖӮе®ғдёҚйңҖиҰҒжү«жҸҸе…ЁеұҖж•°жҚ®е·Із»ҸзҺ°жңүзҡ„з°ҮгҖӮ
з®—жі•жөҒзЁӢ
иҒҡзұ»зү№еҫҒ CF=пјҲNпјҢLSпјҢSSпјүпјҢе…¶дёӯ N д»ЈиЎЁз°ҮдёӯзӮ№зҡ„дёӘж•°пјҢLS д»ЈиЎЁз°Үдёӯд»ЈиЎЁз°Үдёӯеҗ„зӮ№зәҝжҖ§е’ҢпјҢSS д»ЈиЎЁз°Үдёӯеҗ„зӮ№зҡ„е№іж–№е’Ңи·қзҰ»гҖӮиҒҡзұ»зү№еҫҒиў«еә”з”ЁдәҺ CF ж ‘дёӯпјҢCF ж ‘жҳҜдёҖз§Қй«ҳеәҰе№іиЎЎж ‘пјҢе®ғе…·жңүдёӨдёӘеҸӮж•°пјҡе№іиЎЎеӣ еӯҗ B е’Ңз°ҮеҚҠеҫ„йҳҲеҖј TгҖӮе…¶дёӯе№іиЎЎеӣ еӯҗ B д»ЈиЎЁжҜҸдёҖдёӘйқһеҸ¶еӯҗиҠӮзӮ№жңҖеӨҡиғҪеӨҹеј•е…Ҙ B дёӘе®һдҪ“жқЎзӣ®гҖӮ
еҸ¶еӯҗиҠӮзӮ№жңҖеӨҡеҸӘиғҪеҢ…еҗ« L дёӘе®һдҪ“жқЎзӣ®пјҢ并且е®ғ们具жңүеүҚеҗ‘еҗҺеҗ‘жҢҮй’ҲпјҢиҝҷж ·еҸҜд»ҘеҪјжӯӨй“ҫжҺҘиө·жқҘгҖӮ
ж ‘зҡ„еӨ§е°ҸеҸ–еҶідәҺз°ҮеҚҠеҫ„йҳҲеҖј T зҡ„еӨ§е°ҸгҖӮ
д»Һж №иҠӮзӮ№ејҖе§ӢпјҢйҖ’еҪ’жҹҘжүҫдёҺиҰҒжҸ’е…Ҙзҡ„ж•°жҚ®зӮ№и·қзҰ»жңҖиҝ‘зҡ„еҸ¶еӯҗиҠӮзӮ№дёӯзҡ„е®һдҪ“жқЎзӣ®пјҢйҖ’еҪ’иҝҮзЁӢйҖүжӢ©жңҖзҹӯи·Ҝеҫ„гҖӮ
жҜ”иҫғдёҠиҝ°и®Ўз®—еҮәзҡ„ж•°жҚ®зӮ№дёҺеҸ¶еӯҗиҠӮзӮ№дёӯе®һдҪ“жқЎзӣ®й—ҙзҡ„жңҖиҝ‘и·қзҰ»жҳҜеҗҰе°ҸеҸ¶з°ҮеҚҠеҫ„йҳҲеҖј TпјҢе°ҸдәҺеҲҷеҗёж”¶иҜҘж•°жҚ®зӮ№гҖӮеҗҰеҲҷжү§иЎҢдёӢдёҖжӯҘгҖӮ
еҲӨж–ӯеҪ“еүҚжқЎзӣ®жүҖеңЁзҡ„еҸ¶иҠӮзӮ№дёӘж•°жҳҜеҗҰе°ҸдәҺ LпјҢиӢҘе°ҸдәҺеҲҷзӣҙжҺҘе°ҶиҜҘж•°жҚ®зӮ№жҸ’е…ҘеҪ“еүҚзӮ№гҖӮеҗҰеҲҷеҲҶиЈӮеҸ¶еӯҗиҠӮзӮ№пјҢеҲҶиЈӮиҝҮзЁӢжҳҜе°ҶеҸ¶еӯҗиҠӮзӮ№дёӯи·қзҰ»жңҖиҝңзҡ„дёӨдёӘе®һдҪ“жқЎзӣ®еҸҳдёәж–°зҡ„дёӨдёӘеҸ¶еӯҗиҠӮзӮ№пјҢе…¶д»–жқЎзӣ®еҲҷж №жҚ®и·қзҰ»жңҖиҝ‘еҺҹеҲҷйҮҚж–°еҲҶй…ҚеҲ°иҝҷдёӨдёӘж–°зҡ„еҸ¶еӯҗиҠӮзӮ№дёӯгҖӮеҲ йҷӨеҺҹжқҘзҡ„еҸ¶еӯҗиҠӮзӮ№е№¶жӣҙж–° CF ж ‘гҖӮ
иӢҘдёҚиғҪе°ҶжүҖжңүж•°жҚ®зӮ№еҠ е…Ҙ CF ж ‘дёӯпјҢеҲҷиҖғиҷ‘еўһеҠ з°ҮеҚҠеҫ„йҳҲеҖј TпјҢ并йҮҚж–°жӣҙж–° CF ж ‘зӣҙиҮіжүҖжңүзҡ„ж•°жҚ®зӮ№иў«еҠ е…Ҙ CF ж ‘дёәжӯўгҖӮ
CURE з®—жі•
з®—жі•жөҒзЁӢ
еңЁж•°жҚ®йӣҶдёӯйҖүжӢ©ж ·жң¬ж•°жҚ®гҖӮ
е°ҶдёҠиҝ°ж ·жң¬ж•°жҚ®еҲ’еҲҶдёә P дёӘеҗҢж ·еӨ§е°Ҹзҡ„еҲ’еҲҶгҖӮ
е°ҶжҜҸдёӘеҲ’еҲҶдёӯзҡ„зӮ№иҒҡжҲҗ m/pq дёӘз°ҮпјҢе…ұеҫ—еҲ° m/q дёӘз°ҮгҖӮиҝҮзЁӢдёӯйңҖеҲ йҷӨеҷӘеЈ°зӮ№гҖӮ
еҜ№дёҠиҝ° m/q дёӘз°ҮиҝӣиЎҢиҒҡзұ»зӣҙиҮіеү©дёӢ k дёӘз°ҮгҖӮ
继з»ӯеҲ йҷӨзҰ»зҫӨзӮ№гҖӮ
е°Ҷеү©дёӢзҡ„зӮ№жҢҮжҙҫеҲ°жңҖиҝ‘зҡ„з°Үе®ҢжҲҗиҒҡзұ»иҝҮзЁӢгҖӮ
иҒҡзұ»з®—жі•жҳҜж•°жҚ®жҢ–жҺҳз®—жі•дёӯжңҖдёәйҮҚиҰҒзҡ„йғЁеҲҶд№ӢдёҖпјҢз®—жі•з§Қзұ»з№ҒеӨҡпјҢеә”з”ЁеңәжҷҜд№ҹеҗ„жңүдёҚеҗҢпјҢжң¬ж–Үз« жҸҗеҲ°зҡ„иҒҡзұ»з®—жі•дёәеёёи§Ғеёёз”Ёзҡ„дёҖдәӣиҫғдёәеҹәжң¬зҡ„з®—жі•пјҢеҜ№дәҺе…¶д»–зҡ„иҒҡзұ»з®—жі•пјҢеҰӮжңҖе°Ҹз”ҹжҲҗж ‘иҒҡзұ»пјҢCLIQUEпјҢDENCLUEпјҢSOM зӯүзӯүеҰӮжңүе…ҙи¶ЈпјҢиҜ»иҖ…еҸҜд»ҘиҮӘиЎҢжҹҘжүҫзӣёе…іиө„ж–ҷиҝӣиЎҢеӯҰд№ гҖӮжң¬ж–Үж—ЁеңЁжҸҗй«ҳиҜ»иҖ…еҜ№з®—жі•жң¬иә«зҡ„зҗҶи§ЈпјҢд»Јз Ғе®һзҺ°иҝҮзЁӢеҸҠз»“жһңжү“еҚ°иғҪеӨҹжӣҙеҘҪзҡ„её®еҠ©иҜ»иҖ…еү–жһҗз®—жі•пјҢдҪҝиҜ»иҖ…иғҪеӨҹжӣҙеҝ«зҡ„е…Ҙ门并жҺҢжҸЎеҹәжң¬зҡ„иҒҡзұ»з®—жі•гҖӮ
- зӣёе…іжҺЁиҚҗ
- зғӯзӮ№жҺЁиҚҗ
- и
-
жңәеҷЁеӯҰд№ д№ӢеҲҶзұ»еҲҶжһҗдёҺиҒҡзұ»еҲҶжһҗ2023-03-27 6580
-
еҹәдәҺPythonзҡ„иҒҡзұ»еҲҶжһҗеҸҠе…¶еә”з”Ёз®Җд»Ӣ2021-05-28 884
-
еҹәдәҺFPGAзҡ„е®ҡзӮ№LMSз®—жі•зҡ„е®һзҺ°и®Іи§Ј2021-04-28 995
-
MatlabжҸҗдҫӣзҡ„дёӨз§ҚиҒҡзұ»еҲҶжһҗ2020-04-29 21629
-
иҒҡзұ»еҲҶжһҗж–№жі•жңүе“Әдәӣ2018-02-23 19082
-
spssиҒҡзұ»еҲҶжһҗж ‘зҠ¶еӣҫ2018-02-12 48951
-
еҹәдәҺHadoopдёҺиҒҡзұ»еҲҶжһҗзҡ„зҪ‘з»ңж—Ҙеҝ—еҲҶжһҗжЁЎеһӢ2017-12-07 826
-
еҹәдәҺдё»еҠЁеӯҰд№ зҡ„еҫ®еҚҡиҒҡзұ»еҲҶжһҗ2017-01-07 890
-
еҹәдәҺGT4зҡ„иҒҡзұ»еҲҶжһҗз®—жі•з ”з©¶2014-02-13 1307
-
жҳҹеә§еӣҫиҒҡзұ»еҲҶжһҗзҡ„QAMдҝЎеҸ·и°ғеҲ¶иҜҶеҲ«з®—жі•еҸҠDSPе®һзҺ°2010-05-08 3220
-
е®һз”Ёз®—жі•еҲҶжһҗдёҺзЁӢеәҸи®ҫи®Ў2009-10-23 805
е…ЁйғЁ0жқЎиҜ„и®ә

еҝ«жқҘеҸ‘иЎЁдёҖдёӢдҪ зҡ„иҜ„и®әеҗ§ !

