

半导体光增益与放大特性
描述
在半导体中,光子的放射是由电子和电洞借由垂直跃迁所达成的,我们可以把具有相同k值的电子一电洞看成一种新的激发粒子,一旦电子电洞复合放出光子后,此激发粒子便回到低能态的基态中,此种新激发粒子的能量动量关系,可由其能量动量关系曲线中得出激发粒子的有效质量,称之为缩减有效质量(reduced effective mass),及激发粒子的能态密度,称之为联合能态密度(joint density of State),图2-4中导电带(conduction band) 和价电带(valence band)中的有效质量分别为mc 与mv。其中缩减等效质量和mc 与mv的关系为:
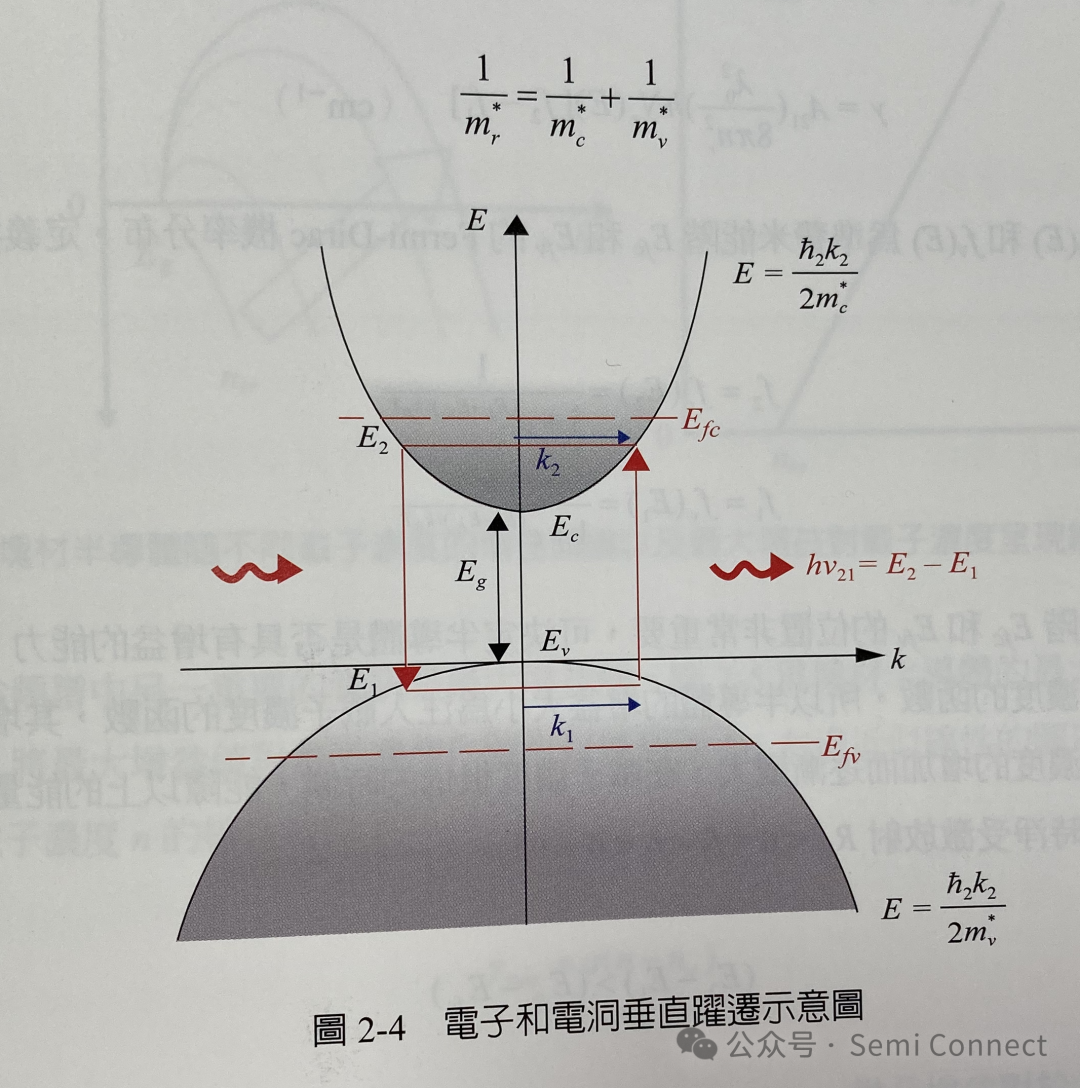
而图2-4中准费米能阶为Efc和Efv,其之间的能量差异是由注入的电子与电洞的多寡所决定,当主动层中的载子浓度愈高,准费米能阶之间的能量差异愈大,反之则会减少。
雷射主要是架构在光放大器的基础上,而“增益”是指把光放大的程度,在半导体雷射中,利用主动层中载子浓度变化来改变材料光学特性,当高载子注入时,电子与电洞注入主动层,产生雷射增益,达到居量反转,最后放出雷射光。增益系数y定义为:

我们可借用原子二能阶系统以 Einstein模型来描述在半导体中具有相同k值的电子一电洞与光的交互作用,可得到另一种半导体块材增益系数频谱表示式;
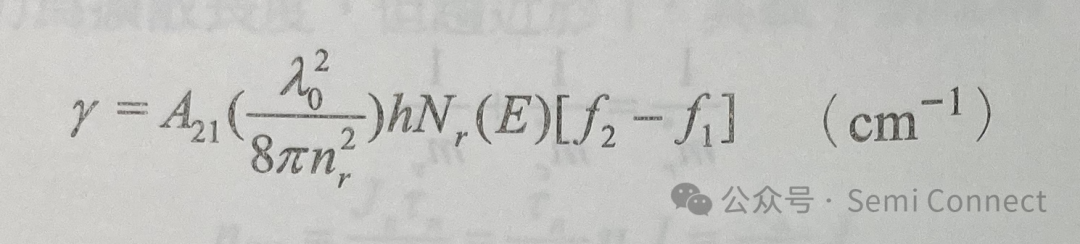
上式中fc(E)和fv(E)为准费米能阶Efc和Efv的Fermi-Dirac 机率分布。定义如下;
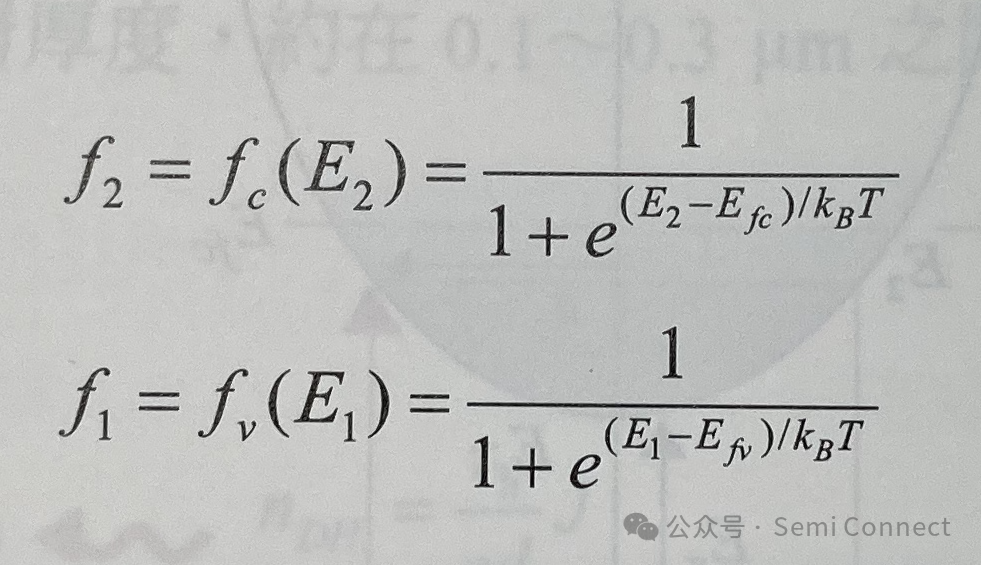
准费米能阶Efc和Efv的位置非常重要,可决定半导体是否具有增益的能力,Efc和Efv又是注入载子浓度的函数,所以半导体的增益大小为注入载子浓度的函数,其增益频谱会随着注入载子浓度的增加而逐渐变大,在载子浓度很低的时候,能隙以上的能量都呈现吸收的情况,此时净受激放射Rst<0,f2-f1<0,即
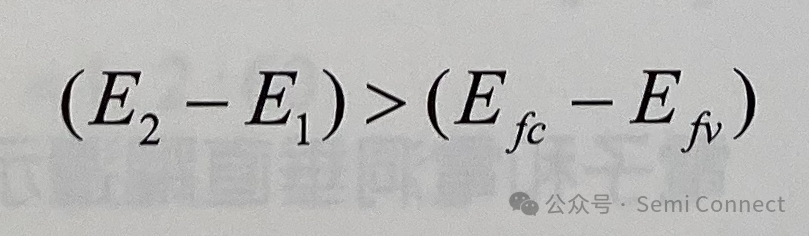
而当增益开始大于零时,净受激放射Rst=0,光不会被放大,也不会被吸收,此时hv=E2-E1=Efc - Efv,f2-f1=0,我们称为透明条件(transparency condition),此时的载子浓度被称为透明载子浓度(transparency carrier density)ntr。当注入的载子浓度大于ntr以上时,半导体增益值愈来愈高与增益频宽愈来愈大,但只有那些能量介于Eg和(Efc - Efv)之间的光子通过此半导体时,才会有被放大的现象,此时Rst>0,表现出增益现象,f2-f1>0化简可得
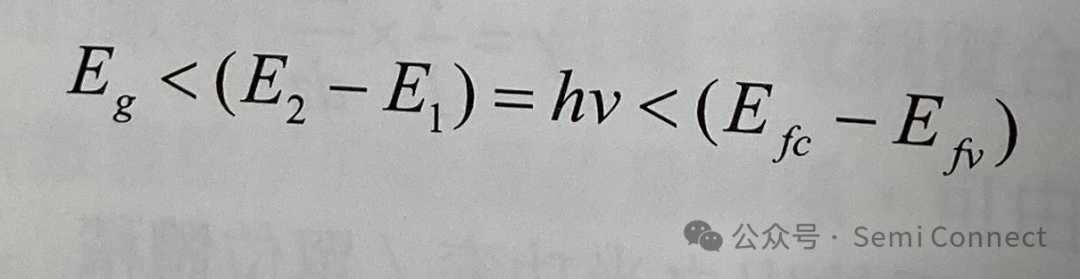
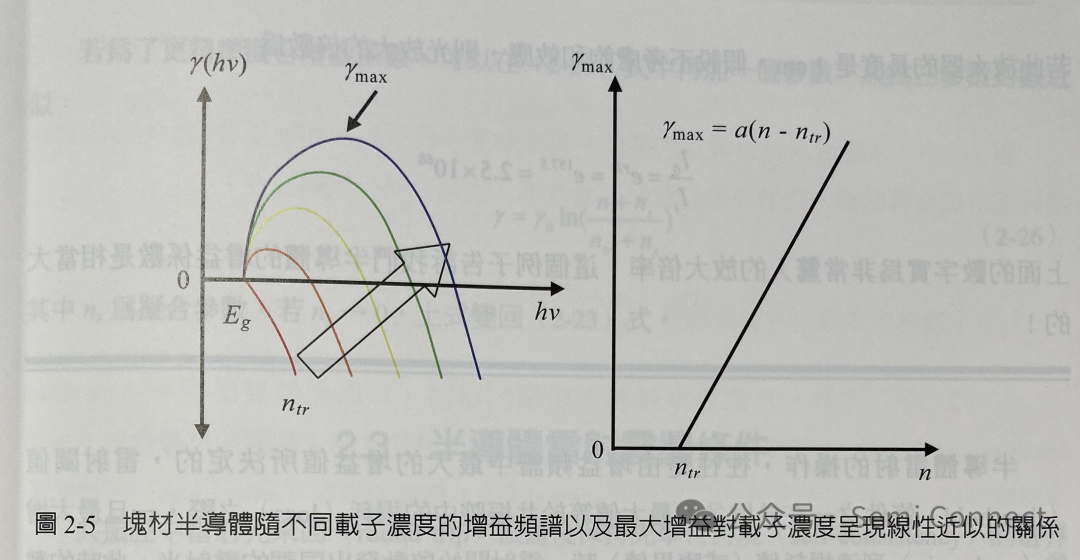
增益频谱中另一重要的资讯是最大增盆值。图2-5为块材半导体的最大增益值对载子浓度图,将最大增益值对载子浓度作图可以得到图2-5 右边近似线性的图形,为最大增盆Ymax和载子浓度n 的线性近似:
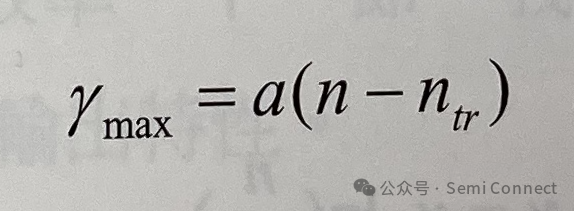
-
半导体光放大器SOA增益特性仿真2025-11-26 301
-
SOA增益饱和特性仿真分析2025-10-31 355
-
一文带你看懂什么是SOA半导体光放大器?半导体光放大器的分类及应用 SOA半导体光放大器介绍2024-04-24 6548
-
soa半导体光放大器原理 soa半导体光放大器可以当光开关吗2024-02-18 2865
-
SOA半导体光放大器原理 SOA半导体光放大器的缺点2024-01-30 2509
-
soa光放大器原理 soa光放大器增益测试2024-01-25 6553
-
SOA半导体光放大器有几个增益波段2024-01-17 1977
-
soa光放大器增益测试2024-01-10 2110
-
半导体光放大器SOA原理2023-07-05 1790
-
半导体光放大器SOA技术及应用简介2023-02-16 8014
-
半导体光放大器的工作原理_半导体光放大器的优缺点2020-03-02 21563
-
半导体的导电特性2017-07-28 2950
-
半导体材料的特性与参数2013-01-28 9019
全部0条评论

快来发表一下你的评论吧 !

